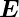 - und
- und 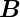 -Feldern
bestimmt man e∕me.
-Feldern
bestimmt man e∕me.
Seit J.J. Thomson [Tho97] das Elektron entdeckt hatte, ist es eines der am genauesten untersuchten Elementarteilchen. Die Kennwerte des Elektrons werden mit den folgenden Methoden bestimmt:
Die Ladung eines Elektrons kann auf elektrochemischem Wege bestimmt werden:
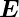 - und
- und 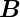 -Feldern
bestimmt man e∕me.
-Feldern
bestimmt man e∕me.
Der Millikan-Versuch [Mil11, Mil13, Hol00] ermöglicht eine direkte Bestimmung von e. Millikans Schlüsselidee war, über die viskose Reibung von kleinen Öltröpfchen die Kraft eines elektrischen Feldes auf Ladungen zu bestimmen.
__________________________________________________________________________
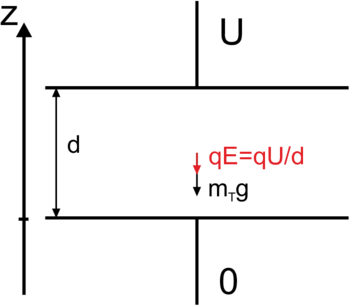
_____________________________________________________________________
Der Versuch wird in einer Anordnung wie in Abbildung 4.2.1.1 durchgeführt.
Ein Öltröpfchen mit dem Durchmesser 2r
und der Masse mT = 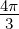 ϱT r3 wird zwischen
die Platten eines Kondensators (Abstand
d) gebracht. Auf dem Öltröpfchen befindet
sich die Ladung q. Unter dem Einfluss
der Gravitation FG, des Auftriebs FA in
Luft (Dichte ϱL) und des elektrischen Feldes
FE bewegt sich das Öltröpfchen mit der
konstanten Geschwindigkeit v, gegeben durch
die Stokesche Reibungskraft FS .
ϱT r3 wird zwischen
die Platten eines Kondensators (Abstand
d) gebracht. Auf dem Öltröpfchen befindet
sich die Ladung q. Unter dem Einfluss
der Gravitation FG, des Auftriebs FA in
Luft (Dichte ϱL) und des elektrischen Feldes
FE bewegt sich das Öltröpfchen mit der
konstanten Geschwindigkeit v, gegeben durch
die Stokesche Reibungskraft FS .
Dabei treten die folgenden Kräfte auf:
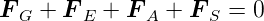 | (4.1) |
Stokes Gesetz für eine laminare Strömung sagt:
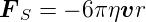 | (4.2) |
Die elektrostatische Kraft ist:
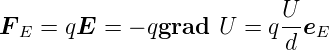 | (4.3) |
wobei 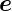 E =
E = 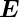 ∕
∕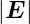 der Einheitsvektor in die Richtung des
elektrischen Feldes ist. Dann muss auch die Gravitation
berücksichtigt werden:
der Einheitsvektor in die Richtung des
elektrischen Feldes ist. Dann muss auch die Gravitation
berücksichtigt werden:
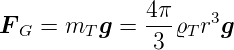 | (4.4) |
Schliesslich haben die Tröpfchen in Luft einen Auftrieb:
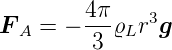 | (4.5) |
Kombiniert man die obigen Gleichungen, erhält man für den Zusammenhang von Ladung und Geschwindigkeit
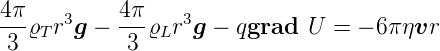 | (4.6) |
Betragsmässig ergibt sich
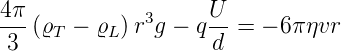 | (4.7) |
und
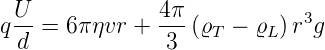 | (4.8) |
Damit kann die Ladung über das elektrische Feld (oder die Spannung), die Dichten, die Viskosität, die Fallstrecke und den Tröpfchendurchmesser bestimmt werden
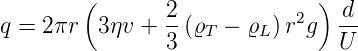 | (4.9) |
Im Einzelnen läuft der Versuch wie folgt ab:
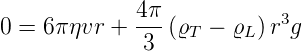
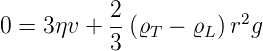
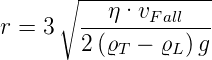 | (4.10) |
was ok ist, da vFall < 0 ist!
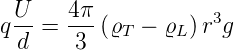
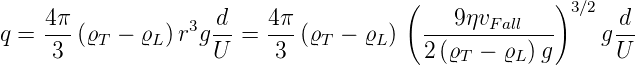
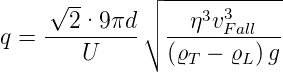 | (4.11) |
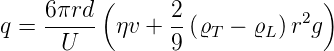 | (4.12) |
Der Schwebezustand ist fast nicht experimentell erreichbar, deshalb misst man im Wesentlichen v(U), wobei U = ±U0 zwei Werte annimmt.
Setzt man (4.10) in Gleichung (4.12) ein, erhalten wir
Hier ist
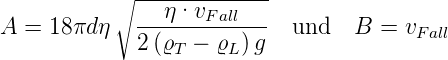 | (4.14) |
Millikan[Mil13] erhielt als Wert für die Elektronenladung e = 1.592·10−19C.
| Versuch zur Vorlesung: | |
| Millikan-Versuch: Ladung von Öltröpfchen (Versuchskarte AT-13) | |
Das Elektron mit seiner kleinen Masse ist eines der Objekte, bei dem quantenmechanische Eigenschaften besonders ausgeprägt sind. Je grösser die Masse eines Objektes, desto eher verhält es sich klassisch. Wenn man annimmt, dass die Selbstenergie des elektrischen Feldes der relativistischen Ruheenergie des Elektrons entspricht, kann ein klassischer Elektronenradius re,class = 2.8·10−15 m bestimmt werden. Belloni [Bel81] zeigt, dass eine andere Überlegung von Fermi auf einen etwa zwölf mal grösseren Elektronenradius führt. Neuere Experimente durch zum Beispiel Dehmelt [Deh88] haben jedoch gezeigt, dass der quantenmechanisch korrektere Radius des Elektrons re,QM < 10−22 m sein muss. Genaueres ist nicht bekannt, es gibt keine abschliessende Aussage über den Elektronenradius. Es kann gut sein, dass ein Elektron eine sehr gute Approximation eines mathematischen Punktteilchen ist, fast eine Divergenz im Raum.
Um den klassischen Elektronenradius zu berechnen, beginnen wir mit der Ladungsdichte ϱel einer homogen geladenen Kugel mit dem Radius r
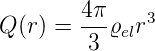
Wenn bei der gleichen Ladungsdichte eine Kugelschale mit der Dicke dr dazugefügt wird, trägt diese eine Ladung
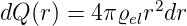
Die Ladung Q wirkt auf eine Probeladung dQ im Abstand r vom Zentrum von Q mit der Kraft
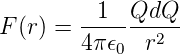
Hält man nun Q und dQ fest und führt dQ vom Unendlichen auf die Distanz r, so muss die folgende Energie zugeführt werden:
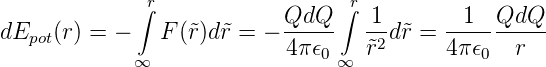
Die gesamte Energie in der homogen geladenen Kugel ist
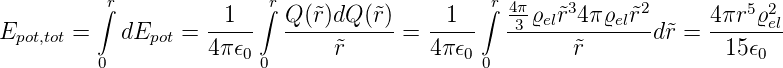 | (4.15) |
Die Ladungsdichte kann mit dem noch unbekannten Elektronenradius re wie folgt berechnet werden:
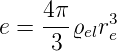
Wir setzen die Ladungsdichte ϱel in (4.15) ein und erhalten so für eine homogen geladene Kugel
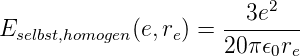 | (4.16) |
Diese Energie setzen wir der relativistischen Ruheenergie der Masse me gleich.
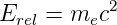 | (4.17) |
Setzen wir Gleichung (4.16) und Gleichung (4.17) gleich und lösen nach dem Elektronenradius re auf, erhalten wir
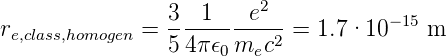 | (4.18) |
Andererseits kann man den klassischen Elektronenradius auch berechnen, wenn man annimmt, dass die gesamte Ladung an der Oberfläche konzentriert sei. Dazu betrachtet man das elektrische Feld einer Ladung e
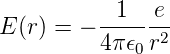
Die Energiedichte dieser Ladung ausserhalb ist
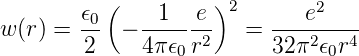
Der Energieinhalt des elektrischen Feldes ausserhalb in Kugelkoordinaten ist
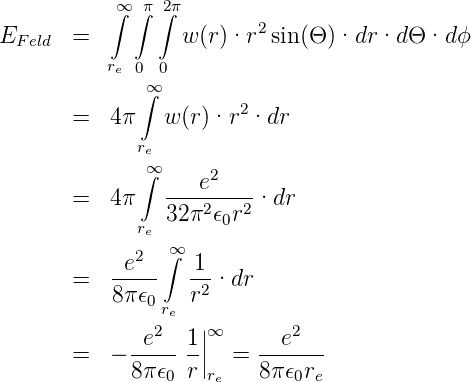
Durch Gleichsetzen mit Gleichung (4.17) erhalten wir
 | (4.19) |
Wir haben also zwei leicht unterschiedliche Resultate für die homogene Ladung und die Oberflächenladung. Sie unterscheiden sich durch die Vorfaktoren 3∕5 und 1∕2. Deshalb, und weil es im cgs-System so schön aussieht definiert man
Der klassische Elektronenradius ist
|
 Lizenzinformationen
Lizenzinformationen