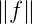5.1  Hilbert-Räume

Zu Beginn folgen einige mathematische Definitionen, die für die korrekte Formulierung der Gesetze und Regeln notwendig sind. Der mathematische Formalismus beruht auf Hilbert-Räumen. Ein Hilbert-Raum wird wie folgt definiert:

H ist ein linearer Vektorraum über dem Raum der komplexen Zahlen ℂ mit den Eigenschaften:

• Wir betrachten zwei Funktionen f und g. Wenn f ∈H und g ∈H, dann ist auch (f + g) ∈H
• Es gibt ein Nullelement 0, so dass (f + 0) = f gilt.
• Es gibt zu f ein symmetrisches Element −f so dass [f + (−f)] = 0
• Das skalare Produkt zweier Elemente f ∈ H und g ∈ H ist als Abbildung H ×H → ℂ :  (f,g) = f·g = ∫ _−∞^+∞f(u)g(u)du definiert.

Die Norm einer beliebigen Funktion f ∈H ist definiert als 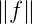= (f∗·f)^1∕2

Weil H ein linearer Vektorraum ist, gelten die folgenden Eigenschaften:

• f·(g₁ + g₂) = f·g₁ + f·g₂
• f·λg = λ(f·g), mit λ ∈ ℂ konstant
• f·f ≥ 0
• f·f = 0 ⇒ f = 0
• g∗·f = (f∗·g)∗

Ein Vektorraum ist vollständig, wenn es für jedes f eine Reihe f₁,f₂,f₃,…f_n → f gibt, so dass lim _n→∞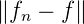 = 0 gilt.

Wenn für das Skalarprodukt von f ∈ H und g ∈ H f·g = 0 gilt, dann sind f und g orthogonal.

5.1.1  Lineare Operatoren

Wenn für einen linearen Operator 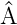und eine Funktion f ∈H die Gleichung 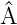f = af gilt, dann f ist Eigenfunktion von 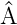. a ist der entsprechende Eigenwert von .

5.1.2  Hermitesche Operatoren

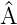Hermitesche Operatoren sind Operatoren, für die die folgende Gleichung gilt

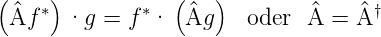(5.1)

Zum Beispiel sind die Operatoren 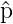_x = (ℏ∕i)(∂∕∂x) und 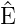= i(∂∕∂t) hermitesch.

Die Eigenfunktionen eines hermiteschen Operators sind orthogonal und die dazugehörigen Eigenwerte sind reell.