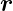 ,t). Wir werden sehen, dass ψ(
,t). Wir werden sehen, dass ψ(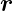 ,t) nicht
direkt beobachtet werden kann.
,t) nicht
direkt beobachtet werden kann.

Wir haben gesehen, dass Materieteilchen bei gewissen
Experimenten Interferenzerscheinungen zeigen. Wir brauchen
also eine konsistente Beschreibung von Materieteilchen als
Wellen. Die Schrödingergleichung ist eine Gleichung für eine
Wellenfunktion ψ(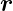 ,t). Wir werden sehen, dass ψ(
,t). Wir werden sehen, dass ψ(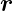 ,t) nicht
direkt beobachtet werden kann.
,t) nicht
direkt beobachtet werden kann.
Wir leiten die eindimensionale Schrödingergleichung in
den Koordinaten (x,t) ∈ ℝ her, indem wir den Ansatz
ψ(x) = A exp ![[i(kx − ωt)]](ap-2018316x.png) verwenden. Wir erinnern uns an die
de Broglie-Beziehung p = h∕λ = ℏk aus Gleichung (4.1). Die
erste und die zweite örtliche Ableitung unseres Ansatzes
sind
verwenden. Wir erinnern uns an die
de Broglie-Beziehung p = h∕λ = ℏk aus Gleichung (4.1). Die
erste und die zweite örtliche Ableitung unseres Ansatzes
sind
![-∂-ψ = ikA exp [i(kx − ωt )] = ikψ
∂x](ap-2018317x.png) | (5.1) |
und
![∂2 2 2
∂x2ψ = (ik) A exp [i(kx − ωt)] = − k ψ](ap-2018318x.png) | (5.2) |
Unser Ansatz ψ(x,t) = A exp ![[i(kx − ωt )]](ap-2018319x.png) , mit k = 2π∕λ und
ω = 2πν, ist auch eine Lösung der Wellengleichung
, mit k = 2π∕λ und
ω = 2πν, ist auch eine Lösung der Wellengleichung
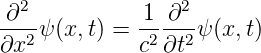 | (5.3) |
wobei c = λν = ω∕k die Ausbreitungsgeschwindigkeit ist. Gleichzeitig ist
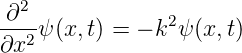 | (5.4) |
und
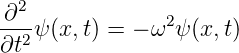 | (5.5) |
Nach Planck setzen wir für die Energie E = ℏω an. Das Teilchen habe den de Broglie-Impuls p = ℏk. Wir verwenden die relativistische Energie-Impulsbeziehung und entwickeln in eine Reihe.
 | (5.6) |
wobei γ = 1∕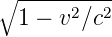 ist.
ist.
Für nichtrelativistische Geschwindigkeiten v « c können relativistische Effekte vernachlässigt werden. Dann ist die kinetische Energie
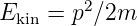 | (5.7) |
mit p = mv = ℏk. Andererseits kann die kinetische Energie T auch geschrieben werden als T = E − V = (ℏ2k2)∕(2m) mit k2 = 2m(E − V )∕ℏ2. Wir erhalten also
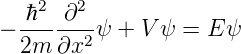 | (5.8) |
Dieser Weg zur Herleitung der Schrödingergleichung ist Schrödingers originaler Weg zur Beschreibung von Materiewellen.
Die Schrödingergleichung kann auch mit einer zweiten
Methode hergeleitet werden. Das Hamiltonsche Extremalprinzip
fordert, dass die Wirkung eines Systems beschrieben durch
die Lagrange-Funktion L(q,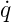 ,t) extremal ist, das
heisst
,t) extremal ist, das
heisst
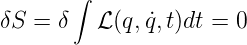 | (5.9) |
Aus dieser Foderung ergibt sich bei einem zeitunabhängigen Potential die Hamilton-Funktion als die Summe der kinetischen und der potentiellen Energie
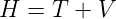 | (5.10) |
V soll hier nur eine Funktion von x sein. Die kinetische Energie ist T = p2∕(2m), wobei p der Impuls eines punktförmigen Teilchens mit der Masse m ist. Wir wissen nach Planck, dass die Energie einer Welle E = ℏω ist. Der Impuls kann gleichzeitig auch als p = ℏk geschrieben werden. Wenn sich ein Teilchen mit der Masse m bewegt, kann ihm eine de Broglie-Wellenlänge λdB = h∕p zugeschrieben werden. Äquivalent zu (5.1) und (5.2), aber universeller, sind die hier angegebenen Gleichungen
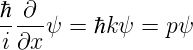 | (5.11) |
oder
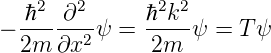 | (5.12) |
Wir definieren den Impulsoperator
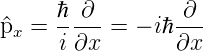 | (5.13) |
und den Operator der kinetischen Energie
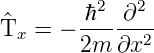 | (5.14) |
Wir wollen nun noch die Zeitabhängigkeit bestimmen. Die erste zeitliche Ableitung von ψ ist
![∂ψ ∂ψ
--- = − iωA exp [i(kx− ωt )] = − iωψ E==⇒ℏω iℏ --- = iℏ(− iω)ψ = E ψ = ^E ψ
∂t ∂t](ap-2018334x.png) | (5.15) |
Den Operator der Gesamtenergie E definieren wir deshalb so:
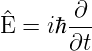 | (5.16) |
Wenn  zeitunabhängig ist, können wir den Operator für die
Hamiltonfunktion definieren
zeitunabhängig ist, können wir den Operator für die
Hamiltonfunktion definieren
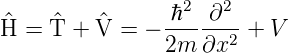 | (5.17) |
wenn 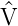 = V ist.
= V ist.
Wenn wir die Gesamtenergie gleich der Hamiltonfunktion setzen,
also 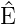 =
=  +
+  =
= 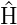 , bekommen wir die Schrödingergleichung
als Analogon zur klassischen Hamilton-Funktion H = T + V .
Operatoren müssen immer auf etwas wirken, hier auf die
Wellenfunktion ψ.
, bekommen wir die Schrödingergleichung
als Analogon zur klassischen Hamilton-Funktion H = T + V .
Operatoren müssen immer auf etwas wirken, hier auf die
Wellenfunktion ψ.
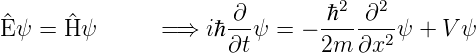 | (5.18) |
Wir haben in dieser Herleitung angenommen, dass die potentielle Energie zeitlich konstant ist. Dann hat der Hamiltonoperator Eigenwerte. Wir können schreiben:
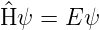 | (5.19) |
Dies ist die stationäre, zeitunabhängige Schrödingergleichung. Die Lösungen der Gleichungen sind harmonische Wellen
![ψ (x,t) = A exp [i(kx − ωt)] = A exp (ikx )exp (− iωt )](ap-2018345x.png)
Die Lösung der Schrödingergleichung, die Wellenfunktion ψ(x,t) kann nicht direkt beobachtet werden. Nach der Kopenhagener Interpretation ist das Skalarprodukt
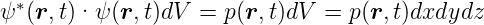 | (5.20) |
gleich der Wahrscheinlichkeit, das System beschrieben
durch ψ(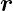 ,t) zur Zeit t am Ort
,t) zur Zeit t am Ort 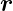 im Volumen dV = dxdydz
zu finden.
im Volumen dV = dxdydz
zu finden.
Zum Beispiel hat ein Teilchen in einem unendlich hohen Potentialkasten die Wellenfunktion
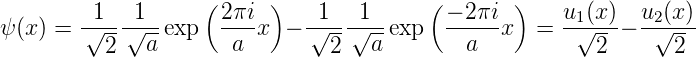 | (5.21) |
Die Wahrscheinlichkeit, ein Teilchen mit der Teilwellenfunktion u1 oder u2 im Potentialkasten zu finden, ist
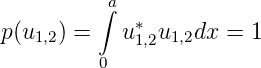 | (5.22) |
Mit einer Wahrscheinlichkeit von 1∕2 misst man Teilchen,
die nach links oder rechts laufen. Dies heisst, dass der
Vorfaktor von u1 und u2 1∕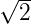 ist. Man kann nachrechnen,
dass auch
ist. Man kann nachrechnen,
dass auch
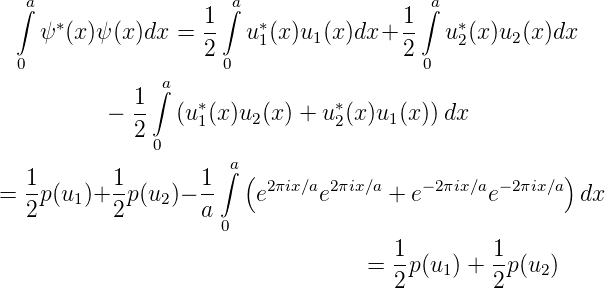 | (5.23) |
Wenn wir nun den Erwartungswert eines Operators
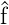 berechnen wollen, müssen wir den gewichteten Mittelwert
ausrechnen. Für übliche Funktionen f(x) mit der
Gewichtsfunktion g(x) ((g(x) ≥ 0) ∧ (g(x) nicht identisch = 0) )
ist dies
berechnen wollen, müssen wir den gewichteten Mittelwert
ausrechnen. Für übliche Funktionen f(x) mit der
Gewichtsfunktion g(x) ((g(x) ≥ 0) ∧ (g(x) nicht identisch = 0) )
ist dies
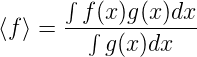 | (5.24) |
In unserem Falle ist die Gewichtsfunktion g(x) = p(x) = ψ∗(x)·ψ(x), die Wahrscheinlichkeitsdichte. Da die Wahrscheinlichkeitsdichten normiert sind, ist ∫ g(x)dx = ∫ ψ∗ψdx = 1. Wir erhalten für den Erwartungswert der Funktion f
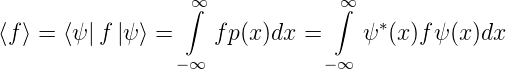 | (5.25) |
Wenn 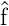 ein Operator ist, muss der Erwartungswert
ein Operator ist, muss der Erwartungswert
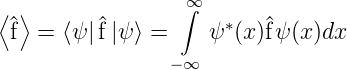 | (5.26) |
sein.
___________________________________________________________________________
| Grösse | Erwartungswert |
| Ort x | 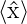 = ∫
−∞∞ψ∗ = ∫
−∞∞ψ∗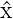 ψdx = ∫
−∞∞x ψdx = ∫
−∞∞x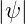 2dx = 2dx = 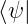 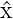 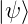 |
| Potential V | 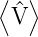 = ∫
−∞∞ψ∗ = ∫
−∞∞ψ∗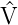 ψdx = ∫
−∞∞V ψdx = ∫
−∞∞V 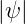 2dx = 2dx = 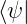  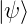 |
| Impuls px | 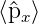 = ∫
−∞∞ψ∗ = ∫
−∞∞ψ∗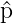 xψdx = ∫
−∞∞ψ∗
xψdx = ∫
−∞∞ψ∗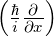 ψdx = ψdx = 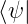 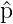 x x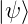 |
| Energie Ekin | 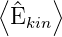 = ∫
−∞∞ψ∗ = ∫
−∞∞ψ∗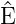 kinψdx = ∫
−∞∞ψ∗
kinψdx = ∫
−∞∞ψ∗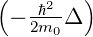 ψdx = ψdx = 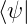 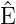 kin kin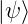 |
_____________________________________________________________________
Tabelle 5.2.3 gibt einige Erwartungswerte an. Verwenden Sie die Tabelle als Anleitung, wie Erwartungwerte berechnet werden sollen. Zur Schreibweise:
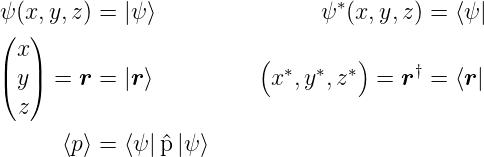
 Lizenzinformationen
Lizenzinformationen