__________________________________________________________________________
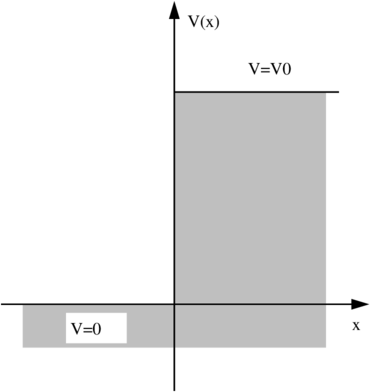
Potentialstufe.
_____________________________________________________________________

__________________________________________________________________________

Potentialstufe.
_____________________________________________________________________
Wir betrachten eine von links auf eine Potentialstufe mit endlicher Energiehöhe einfallende Welle. Dies führt zum Ansatz
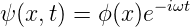
ψ(x,t) ist harmonisch von der Zeit abhängig. Deshalb ist ϕ(x) eine stationäre Lösung der zeitunabhängigen Schrödingergleichung.
Die Lösungen sind abhängig von der Energie des Teilchens (der Welle) unterschiedlich:
Sei ϕj(x) = Aj exp(−ikjx), j = 1 für x < 0 und j = 2 für x > 0, die Ortsfunktion einer einfallenden Welle mit der Energie E, die sich in der positiven Richtung der x-Achse ausbreitet. Ihr Impuls ist p1 = ℏk1 für x < 0 und p2 = ℏk2 für x > 0. Die kinetischen Energien sind T1 = p12∕2m = E und T 2 = p22∕2m = E − V 0. Also haben wir
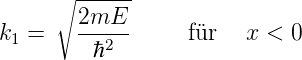 | (5.1) |
und
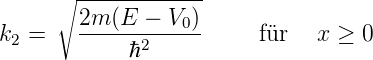 | (5.2) |
Zusätzlich muss für x < 0 eine rücklaufende Welle mit ϕ′1(x) = A′1 exp(ik1x) betrachtet werden
Die Lösungen der Schrödingergleichung müssen zweimal differenzierbar sein, d.h. ϕ und ∂ϕ∕∂x müssen stetig sein für alle x. Die Stetigkeit besagt, dass ϕ(x) und ∂ϕ(x)∕∂x für x = 0 dieselben Werte haben müssen. Die Eigenfunktion ϕ(x) hat für x < 0 zwei Komponenten: Eine sich ausbreitende Welle mit der Amplitude A1 und der Wellenfunktion ϕ1(x) = A1e−ik1x in der positiven Richtung der x-Achse und eine sich ausbreitende Welle (die reflektierte Welle) mit der Amplitude A′1 und der Wellenfunktion ϕ′1(x) = A′1eik1x in der negativen Richtung der x-Achse, beide mit demselben Impuls p1 = ℏk1. Für x > 0 es gibt nur eine harmonische Welle mit der Amplitude A2, der Wellenfunktion ϕ2(x) = A2e−ik2x und dem Impuls p 2 = ℏk2 (transmittierte Welle), die sich in die positive Richtung der x-Achse ausbreitet. Also erhalten wir für den ersten Fall
oder
Wir definieren die folgenden Grössen als Reflexionskoeffizienten
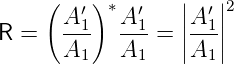 | (5.5) |
und Transmissionskoeffizienten
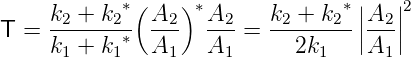 | (5.6) |
Beachten Sie beim Transmissionskoeffizienten die Analogie zu den Fresnelschen Formeln [Mar17, Kap. 6.8]. Diese beiden Koeffizienten beschreiben die Intensität der Reflexion bzw. der Transmission, oder, in anderen Worten, deren Wahrscheinlichkeitsdichte. Die Vorfaktoren haben die gleiche Funktion wie die Dielektrizitätszahlen in den Fresnelschen Formeln der Optik. Die Erhaltung der Gesamtenergie verlangt, dass
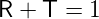 | (5.7) |
ist.
Wenn im Gebiet x > 0 die kinetische Energie kleiner als die potentielle Energie ist (Fall b)) wird der Wellenvektor imaginär
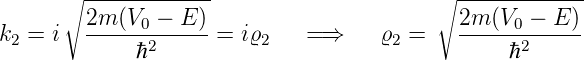 | (5.8) |
Dies bedeutet, dass die Wahrscheinlichkeit das Teilchen für x > 0 zu finden, exponentiell mit x abnimmt. Weiter haben wir
Wie immer ist A1 frei wählbar. Wir erhalten
für den Reflexionskoeffizienten
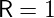 | (5.11) |
und für den Transmissionskoeffizienten
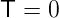 | (5.12) |
Alle Energie wird also reflektiert, aber es gibt im verbotenen Bereich dennoch eine mit der Distanz abnehmende Energiedichte.
__________________________________________________________________________
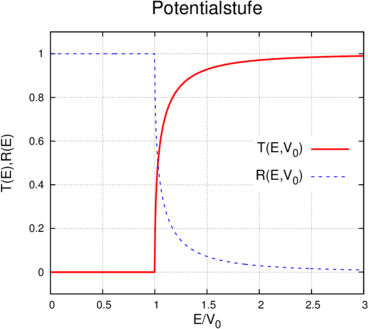
Transmissionskoeffizient T und Reflexionskoeffizient R.
_____________________________________________________________________
_____________________________________________________________________
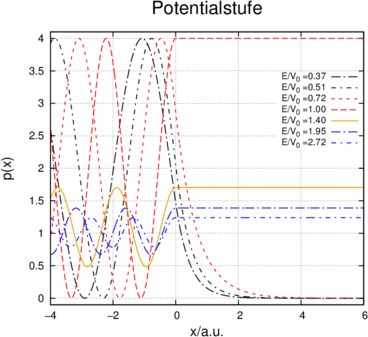
Wahrscheinlichkeitsdichte p(x) = ϕ(x)∗ϕ(x) für verschiedene Verhältnisse von E∕V 0.
_____________________________________________________________________
 Lizenzinformationen
Lizenzinformationen