©2005-2018 Ulm University, Othmar Marti, 
[Nächste
Seite] [Vorherige Seite] [vorheriges Seitenende] [Seitenende]
[Ebene nach oben] [PDF-Datei][Epub-Datei][Andere
Skripte]
6.5 Elektronenspin
6.5.1 Magnetische Spin-Bahn-Kopplung
Elektronen können für viele Untersuchungen als punktförmige
Teilchen angesehen werden. Wenn der klassische Elektronenradius
berechnet wird, wird eine ausgedehnte Ladungswolke
angenommen. Wenn diese Wolke einen Eigendrehimpuls hat,
dann gibt es einen Kreisstrom und damit ein magnetisches
Moment. Der Eigendrehimpuls des Elektrons heisst Spin, der
mit dem Vektor 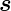 bezeichnet wird. Aus den klassischen
Überlegungen kann aus dem Drehimpuls das magnetische
Moment berechnet werden. Dieses so berechnete Moment ist
jedoch nicht gleich dem gemessenen magnetischen Moment –
ein Zeichen, dass hier die klassische Mechanik die Physik nicht
mehr richtig beschreibt.
bezeichnet wird. Aus den klassischen
Überlegungen kann aus dem Drehimpuls das magnetische
Moment berechnet werden. Dieses so berechnete Moment ist
jedoch nicht gleich dem gemessenen magnetischen Moment –
ein Zeichen, dass hier die klassische Mechanik die Physik nicht
mehr richtig beschreibt.
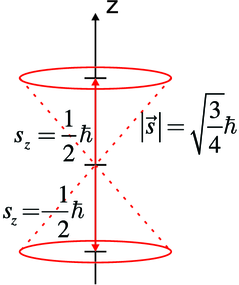
Analog zum Bahndrehimpuls 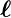 haben wir
haben wir
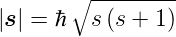 | (6.1) |
__________________________________________________________________________
Elektronenspin 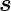 , Betrag |
, Betrag |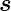 | und z-Komponente sz.
| und z-Komponente sz.
_____________________________________________________________________
Der Zusammenhang zwischen dem Bahndrehimpuls
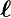 und dem dazugehörigen magnetischen Moment
und dem dazugehörigen magnetischen Moment 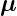 ℓ,
beziehungsweise dem Spin
ℓ,
beziehungsweise dem Spin 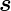 und dessen magnetischem
Moment
und dessen magnetischem
Moment 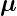 s (siehe auch Abbildung 6.5.1) ist
s (siehe auch Abbildung 6.5.1) ist
wobei
ist. Der Wert von gℓ ist wie erwartet. Der Wert von gs ist
überraschend:
- Das magnetische Moment ist etwa doppelt so
gross wie aus dem Kreisstromargument zu erwarten
gewesen wäre. Dies ist ein quantenmechanischer
Effekt.
- Aus klassischer quantenmechanischer Rechnung
würde gs = 2 folgen. Die Abweichung von 2.0000
ist ein quantenelektrodynamischer Effekt und durch
Messungen auf viele Nachkommastellen bestätigt.
Die Quantenelektrodynamik verknüpft die spezielle
Relativitätstheorie mit der Quantenmechanik.
Gleichzeitig bietet sie eine einheitliche Beschreibung
von Teilchen und Feldern.
Das magnetische Moment des Elektronenspins kann mit
dem Bohrschen Magneton ausgedrückt werden
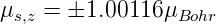 | (6.4) |
Das Verhältnis zwischen Drehimpuls und magnetischem
Moment heisst gyromagnetisches Verhältnis γ = 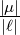 . Das
gyromagnetische Verhältnis für den Bahndrehimpuls und den
Spin ist
. Das
gyromagnetische Verhältnis für den Bahndrehimpuls und den
Spin ist
Der Spin kann zum Beispiel mit dem Stern-Gerlach-Versuch
nachgewiesen, siehe Abbildung 6.4.1.
6.5.2 Feinstruktur und Ein-Elektronen-Atome
Wenn man die Natrium-D-Linie untersucht, findet man,
dass diese in ein Dublett aufgespalten ist. Diese Aufspaltung
nennt man auch Feinstruktur. Sie entsteht, weil der Spin
und der Bahndrehimpuls wechselwirken.
__________________________________________________________________________
_____________________________________________________________________
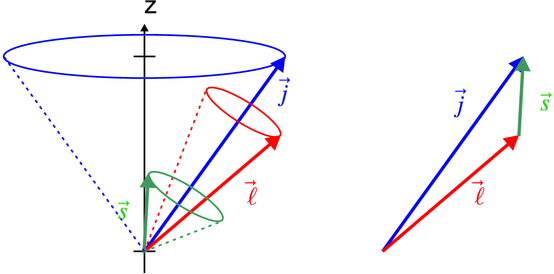
Abbildung 6.5.2 zeigt eine Skizze der Spin-Bahn-Kopplung.
Der Drehimpuls 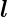 und der Spin
und der Spin 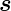 bilden zusammen den
Gesamtdrehimpuls
bilden zusammen den
Gesamtdrehimpuls 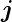 .
.
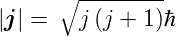 | (6.7) |
mit 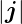 =
= 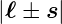 .
.
Wir betrachten ein p-Elektron mit der Bahndrehimpulsquantenzahl
ℓ = 1 und der Spinquantenzahl s = 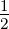 .
.
Wenn der Bahndrehimpuls verschwindet (ℓ = 0) wird die
Quantenzahl des Gesamtdrehimpulses gleich der Quantenzahl
des Spins j = s.
Die magnetische Quantenzahl des Gesamtdrehimpulses, die
die Richtungsquantisierung darstellt, ist
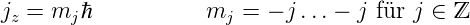 |
(6.10) |
Wie beim Bahndrehimpuls und dem Spin gehört zu jedem
Gesamtdrehimpuls 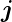 ein magnetisches Moment
ein magnetisches Moment 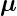 j. Für
optische Übergänge gilt die Auswahlregel: Δj = 0,±1, wobei
der Übergang j = 0 → j = 0 verboten ist.
j. Für
optische Übergänge gilt die Auswahlregel: Δj = 0,±1, wobei
der Übergang j = 0 → j = 0 verboten ist.
__________________________________________________________________________
Spin-Bahnkopplung nach Bohr
_____________________________________________________________________
Zur Berechnung der Spin-Bahn-Aufspaltung im Magnetfeld
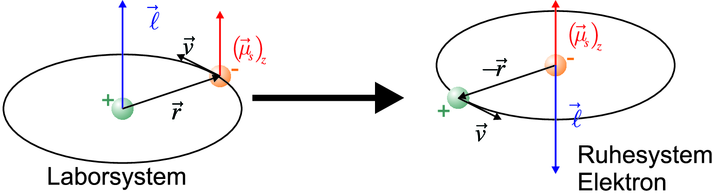
betrachtet man das Atom im Ruhesystem des Elektrons.
Nach Biot-Savart ist das Magnetfeld der Kernladung
+Ze
![B ℓ = + Ze-μ0 [v × (− r)] = − Ze-μ0v × r
4πr3 4πr3](ap-20181017x.png) | (6.11) |
wobei 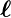 =
= 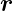 × me
× me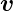 ⇒−
⇒−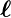 = me
= me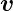 ×
×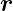 verwendet wurde.
Also ist das Magnetfeld
verwendet wurde.
Also ist das Magnetfeld
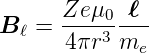 | (6.12) |
Der Spin des Elektrons präzediert um 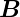 ℓ.
ℓ.
__________________________________________________________________________
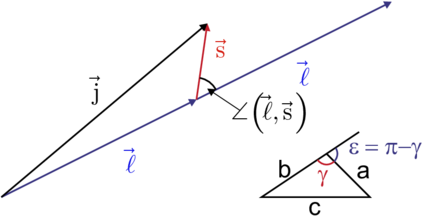
Spinpräzession. Links Skizze, rechts Vektoraddition
_____________________________________________________________________
Nach Gleichung (6.2a) ist das magnetische Moment eines
Spins 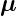 s = −gs
s = −gs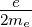
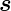 . Setzt man dies in die Gleichung für
die Lageenergie eines magnetischen Moments in einer
magnetischen Induktion Eℓ,s = −
. Setzt man dies in die Gleichung für
die Lageenergie eines magnetischen Moments in einer
magnetischen Induktion Eℓ,s = −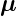 s·
s·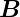 ein, erhält man
ein, erhält man
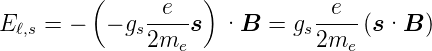 | (6.13) |
Wenn man gs = 2 setzt, erhält man mit Gleichung
(6.12)
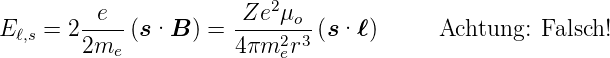 | (6.14) |
Eine genaue relativistische Betrachtung sowie experimentelle
Daten zeigen, dass die Gleichung (6.14) um einen Faktor 1∕2
zu falsch ist. Llewellyn Thomas entdeckte während seiner
Doktorarbeit, dass bei der Rücktransformation aus dem
mitrotierenden Koordinatensystem ins Laborsystem die
relativistische Zeitdilatation berücksichtigt werden muss
[Tho26]. Seine Argumentation (im cgs-System!) war wie
folgt:
Das Elektron präzediert um das externe Magnetfeld mit
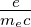
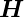 (SI:
(SI: 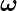 s =
s = 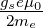
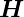 ). Das Elektron bewegt sich mit der
Geschwindigkeit
). Das Elektron bewegt sich mit der
Geschwindigkeit 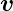 durch die elektrische Verschiebung
durch die elektrische Verschiebung
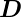 = 𝜀0
= 𝜀0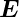 des Kerns, was nach Maxwell zu einem Magnetfeld
des Kerns, was nach Maxwell zu einem Magnetfeld

führt. Die Präzessionswinkelgeschwindigkeit ist dann
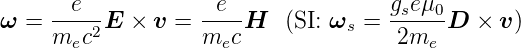
Diese Gleichung ist falsch. Das Elektron erfährt eine
Beschleunigung 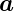 . Man muss eine Lorentz-Transformation
mit der Geschwindigkeit
. Man muss eine Lorentz-Transformation
mit der Geschwindigkeit 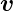 +
+ 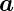 dt verwenden, sowie beachten,
dass der Spin zur Zeit t + dt gedreht ist. Also hat man nach
Thomas eine Geschwindigkeit
dt verwenden, sowie beachten,
dass der Spin zur Zeit t + dt gedreht ist. Also hat man nach
Thomas eine Geschwindigkeit 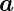 dt und eine Rotation
(1∕2c2)
dt und eine Rotation
(1∕2c2)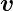 ×
×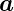 dt zu beachten. Die Präzession wird dann in
erster Näherung durch
dt zu beachten. Die Präzession wird dann in
erster Näherung durch
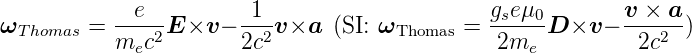
Nun ist die Beschleunigung durch
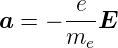
gegeben. Also ist die Präzessionswinkelgeschwindigkeit
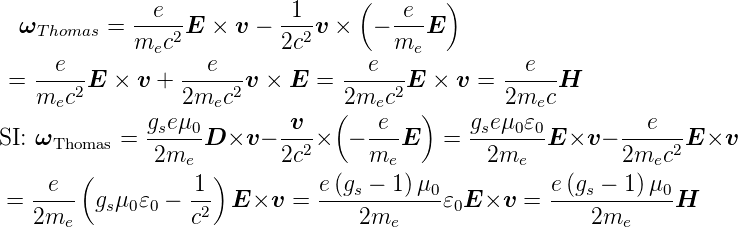 |
(6.15)
|
Die Winkelgeschwindigkeit der Thomaspräzession ist halb
so gross wie die naiv berechnete. Deshalb wird auch die
Energie des magnetischen Momentes halb so gross sein. Aus
der Argumentation von Thomas folgt, dass Gleichung (6.14)
mit dem Faktor 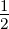 , dem aus der relativistischen Betrachtung
folgenden Thomasfaktor korrigiert werden muss. Wir haben
also für die Energie
, dem aus der relativistischen Betrachtung
folgenden Thomasfaktor korrigiert werden muss. Wir haben
also für die Energie
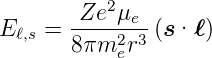 | (6.16) |
__________________________________________________________________________
_____________________________________________________________________
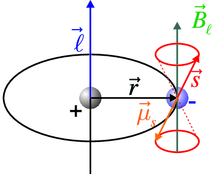
Aus dem Cosinus-Satz für beliebige Dreiecke (siehe
Abbildung 6.5.2)
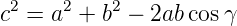 | (6.17) |
erhalten wir mit der Winkelidentität
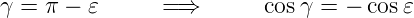 | (6.18) |
und
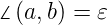 | (6.19) |
schliesslich
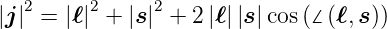 | (6.20) |
Gleichung (6.16) mit dem Zwischenwinkel zwischen 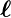 und
und 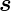 kann also auch
kann also auch
geschrieben werden. Andererseits ist mit Gleichung
(6.20)
Setzt man in Gleichung (6.22) ℓ = 1, s = 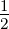 und j =
und j = 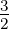 oder
j =
oder
j = 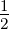 , erhält man die in der Abbildung 6.5.2 gezeigten
Aufspaltung durch die Spin-Bahn-Kopplung.
, erhält man die in der Abbildung 6.5.2 gezeigten
Aufspaltung durch die Spin-Bahn-Kopplung.
__________________________________________________________________________
p-Aufspaltung nach Gleichung (6.22).
_____________________________________________________________________
Der Radius r in der Konstanten a in Gleichung (6.21) ist
rn, der Radius der n-ten Bohrschen Bahn. Für diese Bahn
gilt
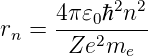 | (6.23) |
und damit
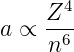
Da es in der Quantenphysik keine festen Bahnen gibt,
muss r−3 durch den mit der Wellenfunktion gewichteten
Wert
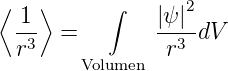 | (6.24) |
ersetzt werden. Man erhält so
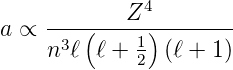 | (6.25) |
6.5.2.1. Elektronenspin-Resonanz
__________________________________________________________________________
_____________________________________________________________________
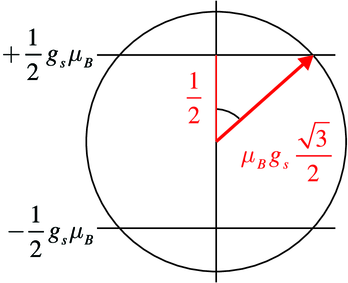
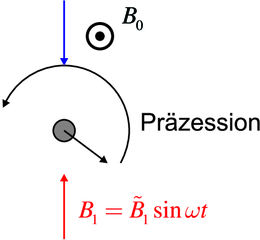
Die präzedierenden Elektronenspins (Skizze in Abbildung
6.5.2.1) wechselwirken besonders stark mit Licht, wenn dieses
in Resonanz mit der Präzessionsfrequenz ist. Die Länge eines
Spins ist
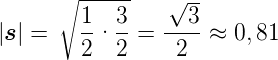 | (6.26) |
Dieser steht dann im Winkel α zum Magnetfeld.
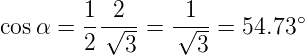 | (6.27) |
Das magnetische Moment eines Spins in Einheiten des
Bohrschen Magnetons μB ist
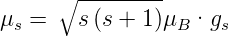 | (6.28) |
wobei seine z-Komponente entlang des Magnetfeldes
durch
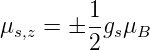 | (6.29) |
gegeben ist. Die beiden möglichen Niveaus haben den
Energieunterschied
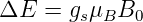 | (6.30) |
__________________________________________________________________________
Situation von oben gesehen
_____________________________________________________________________
Übergänge treten auf, wenn die Energie des Lichtes dem
Energieunterschied der beiden Spinzustände entspricht.
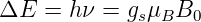 | (6.31) |
oder
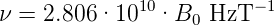 | (6.32) |
Die Präzessionswinkelgeschwindigkeit (Skizze in Abbildung
6.5.2.1) ist
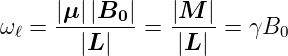 | (6.33) |
mit einem von den atomaren Zuständen abhängigen
Proportionalitätsfaktor γ.
__________________________________________________________________________
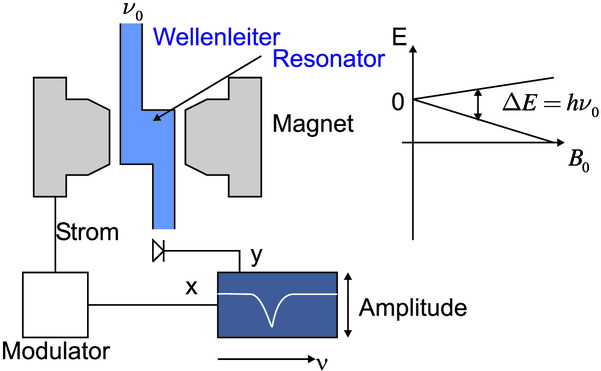
Elektronen-Spin-Resonanz: Aufbau
_____________________________________________________________________
Abbildung 6.5.2.1 zeigt den Aufbau einer ESR-Apparatur.
Die Resonanz der Mikrowellen mit den Spins im Magnetfeld
bewirkt einen Abfall des Signals an der Detektionsdiode.
6.5.3 Zeeman-Effekt
_______________________________________________
_____________________________________________________________________
Die Wechselwirkug der Spins und der Bahndrehimpulse mit
der magnetischen Induktion bewirkt eine Aufspaltung der
Energieniveaus im Magnetfeld.
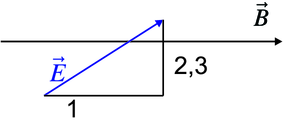
Eine lineare elektromagnetische Schwingung schräg zum
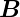 -Feld kann in drei Komponenten aufgeteilt werden.
Diese drei Polarisationskomponenten ergeben wieder
die ursprüngliche elektromagnetische Schwingung. Die
Polarisationskomponenten sind in Abbildung 6.5.3 gezeigt:
-Feld kann in drei Komponenten aufgeteilt werden.
Diese drei Polarisationskomponenten ergeben wieder
die ursprüngliche elektromagnetische Schwingung. Die
Polarisationskomponenten sind in Abbildung 6.5.3 gezeigt:
- eine lineare Schwingung parallel zu
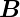 0,
0,
- eine linkszirkulare Schwingung
- und rechtszirkulare Schwingung.
Die magnetische Induktion 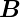 beeinflusst die lineare
Schwingung nicht. Die zirkularen Schwingungen (linkszirkular)
und (rechtszirkular) beschleunigen oder bremsen die
Umlauffrequenz der Elektronen auf ihren Bahnen. Die
Frequenzänderung wird die Larmor-Frequenz genannt. Sie
ist
beeinflusst die lineare
Schwingung nicht. Die zirkularen Schwingungen (linkszirkular)
und (rechtszirkular) beschleunigen oder bremsen die
Umlauffrequenz der Elektronen auf ihren Bahnen. Die
Frequenzänderung wird die Larmor-Frequenz genannt. Sie
ist
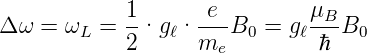 | (6.34) |
Entsprechend den Überlegungen zu (6.2b) ist beim
Bahndrehimpuls ist g = gℓ = 1.
Die Bewegungsgleichung eines Elektrons im Magnetfeld
lautet
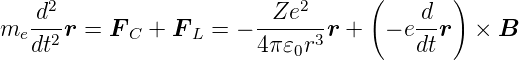 | (6.35) |
Beachten Sie, dass die Ladung des Elektrons negativ ist
und dass die externe magnetische Induktion als B0 = const
angenommen wird.
Allgemein lautet die Identität zwischen Coulombkraft und
Zentripetalkraft
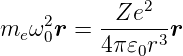 | (6.36) |
Zusammen und auf einer Seite (die z-Komponente der
Lorentzkraft ist null) erhalten wir
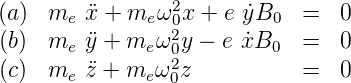 | (6.37) |
Für die z-Komponente folgt aus Gleichung (6.37) (c), dass
z = z0 exp 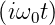 nicht von der magnetischen Induktion
B0 abhängt. Wir setzen u = x + iy und v = x − iy,
oder x =
nicht von der magnetischen Induktion
B0 abhängt. Wir setzen u = x + iy und v = x − iy,
oder x = 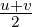 und y =
und y = 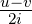 und erhalten aus Gleichung
(6.37) (a) und (b), den Gleichungen für die x- und die
y-Komponenten
und erhalten aus Gleichung
(6.37) (a) und (b), den Gleichungen für die x- und die
y-Komponenten
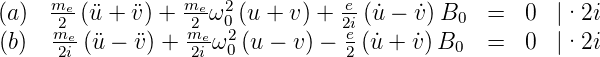 | (6.38) |
Weiter formt man um:
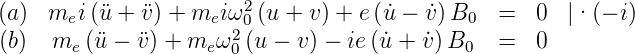 | (6.39) |
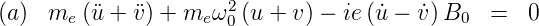 | (6.40) |
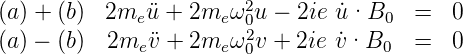 | (6.41) |
Zur Lösung setzen wir an
Eingesetzt in die Gleichungen (6.41) erhalten wir
Wir bekommen also die folgenden Gleichungen für die
Unbekannten im Exponenten:
Wenn B0 « 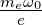 ist, dann sind die Lösungen dieser
Gleichungssysteme
ist, dann sind die Lösungen dieser
Gleichungssysteme
Wenn wir bei ω0 nur das positive Vorzeichen nehmen,
erhalten wir
Die Kreisfrequenz spaltet sich dann wie folgt auf:
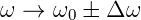 | (6.47) |
mit
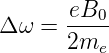 | (6.48) |
Dies entspricht einer Frequenz
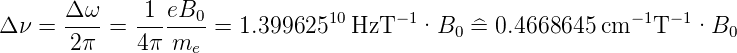 | (6.49) |
Der klassische Zeeman-Effekt bewirkt eine
konstante Frequenzverschiebung.
Es gibt ein Zeeman-Triplett mit
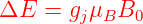 | (6.50) |
|
- Wenn s und ℓ nicht koppeln, haben wir den
normalen Zeeman-Effekt.
- Wenn s und ℓ koppeln, haben wir den anomalen
Zeeman-Effekt.
__________________________________________________________________________
Magnetisches Moment des Gesamtdrehimpulses
_____________________________________________________________________
6.5.3.1. Magnetisches Moment des Gesamtdrehimpulses
Da der g-Faktor des Spins und des Bahndrehimpulses
unterschiedlich sind, ist das magnetische Moment des
Gesamtdrehimpulses nicht antiparallel zum Gesamtdrehimpuls,
sondern präzediert um die Richtung des Gesamtdrehimpulses.
Der Gesamtdrehimpuls 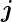 ist parallel zur externen
magnetischen Induktion
ist parallel zur externen
magnetischen Induktion 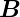 . Da die Präzessionsfrequenz enorm
hoch ist, kann durch eine Messung nur die Projektion von
. Da die Präzessionsfrequenz enorm
hoch ist, kann durch eine Messung nur die Projektion von 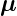 j
auf die Richtung von
j
auf die Richtung von 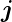 bestimmt werden,
bestimmt werden, 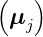 j.
j.
__________________________________________________________________________
Die Winkel zur Berechnung des g-Faktors.
_____________________________________________________________________
Wir definieren die Winkel α = ∠(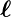 ,
,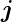 ) und β = ∠(
) und β = ∠(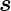 ,
,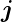 ). In
Abbildung 6.5.3.1 sind die Winkel für einen der beiden Spins
aus Abbildung 6.5.3 eingezeichnet. Die Darstellung zeigt die
Projektionen der magnetischen Momente
). In
Abbildung 6.5.3.1 sind die Winkel für einen der beiden Spins
aus Abbildung 6.5.3 eingezeichnet. Die Darstellung zeigt die
Projektionen der magnetischen Momente 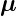 ℓ (lila) und
ℓ (lila) und 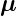 s1
(blau) auf die Richtung des Gesamtdrehimpulses
s1
(blau) auf die Richtung des Gesamtdrehimpulses 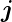 . Wir
können für die Länge des gesamten projizierten magnetischen
Moments
. Wir
können für die Länge des gesamten projizierten magnetischen
Moments 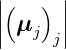 schreiben
schreiben
Eine analoge Darstellung gilt für den anderen Spin aus
Abbildung 6.5.3.
Aus Abbildung 6.5.3.1, rechte Seite, kann man mit
dem Cosinussatz a2 = b2 + c2 − 2bc cos(∠(b,c)) und
(b2 + c2 − a2)(2bc)−1 = cos(∠(b,c)) ablesen
Weiter bekommen wir mit Gleichung (6.51)
Mit der Definition
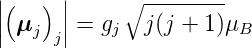 | (6.55) |
bekommen wir für den
| g-Faktor des Gesamtdrehimpulses
|
Das messbare magnetische Moment des Gesamtdrehimpulses
ist dann
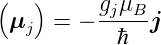 | (6.57) |
Mit Gleichung (6.56) bekommen wir die folgende Tabelle
___________________________________________________________________________
gj als Funktion von ℓ, s und j
_______________________________________________________________
6.5.3.2. Hamiltonoperator für den Zeeman-Effekt
Zur quantenmechanischen Behandlung des Zeeman-Effekts
benötigen wir den Hamiltonoperator im Magnetfeld. Wir
vermuten, dass
sei. Eine Rechnung mit kanonischen Impulsen ergibt mit
den Ersetzungen 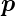 −→
−→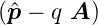
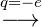
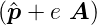 und
und
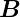 =
=  ×
×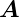
Im Anhang F.1 finden Sie eine Rechnung zur Plausibilität
dieses Hamilton-Operators. Setzen wir den Impulsoperator
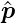 = −iℏgrad = −iℏ
= −iℏgrad = −iℏ ein, erhalten wir
ein, erhalten wir
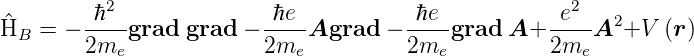 | (6.63) |
Denken Sie daran dass in dieser abgekürzten Schreibweise
grad 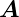 kurz für grad (
kurz für grad (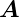 ψ) ist. Ist die magnetische
Induktion in die z-Richtung ausgerichtet, also
ψ) ist. Ist die magnetische
Induktion in die z-Richtung ausgerichtet, also 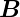 =
= 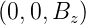 ,
ist ein mögliches Vektorpotential
,
ist ein mögliches Vektorpotential
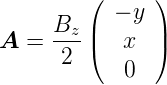 | (6.64) |
Damit lautet Gleichung (6.63)
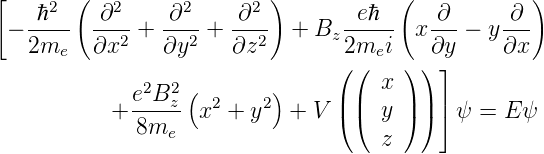 |
(6.65)
|
Wenn das Vektorpotential (Einheit Tm) vom Betrage
nach viel kleiner ist als der Impuls, also e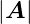 «
« 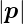 ,
kann der Term mit
,
kann der Term mit 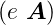 2 oder der Term mit (x2 + y2)
vernachlässigt werden. Dies ist gleichbedeutend mit der
Aussage, dass der Diamagnetismus vernachlässigt wird. Der
Zeeman-Effekt kann dann durch ein Potential ausgedrückt
werden.
2 oder der Term mit (x2 + y2)
vernachlässigt werden. Dies ist gleichbedeutend mit der
Aussage, dass der Diamagnetismus vernachlässigt wird. Der
Zeeman-Effekt kann dann durch ein Potential ausgedrückt
werden.
Nach Gleichung (6.5) und Gleichung (6.10c) ist
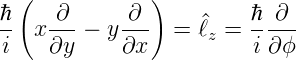
Wenn nun das Potential V (r) kugelsymmetrisch ist, lautet
Gleichung (6.65)
![[ ( ( ) ( ))
ℏ2 1 ∂ 2 ∂ 1 ∂2 1 ∂ ∂
− ---- -2 --- r --- + -2---2----2 + -2-------- sin 𝜃---
2me r ∂r ∂r r sin 𝜃∂ ϕ r ]sin 𝜃∂ 𝜃 ∂ 𝜃
eBz- ℏ-∂-
+ 2m i∂ϕ + V (r) ψ = E ψ
e](ap-20181180x.png) |
(6.66)
|
Gleichung (6.66) kann wie das Wasserstoffatom im
magnetfeldfreien Raum durch den Ansatz (6.13) gelöst
werden. Dies führt zu Gleichung (6.115)
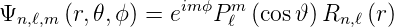
Die Energieeigenwerte sind aber
Hier ist En0 die Energie des n-ten Niveaus im magnetfeldfreien
Raum. Beachten sie, dass zu diesem Zeitpunkt nur mit
Bahndrehimpulsen gerechnet wurde. Gleichung (6.71) gibt die
vollständige Gleichung an
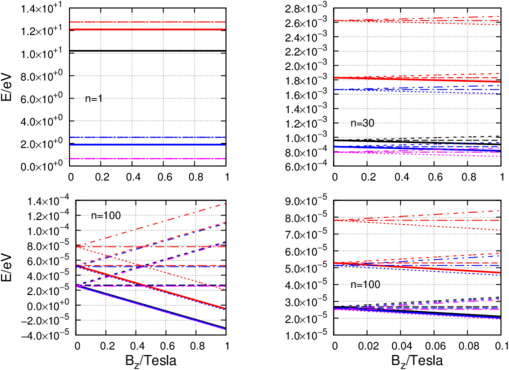
__________________________________________________________________________
Zeeman-Aufspaltung für Übergänge n + 1 → n,
n + 2 → n, n + 2 → n + 1, n + 3 → n, n + 3 → n + 1
und n + 3 → n + 2.
_____________________________________________________________________
6.5.3.3. Hamiltonoperator für den Zeeman-Effekt mit Spins
und Spin-Bahn-Kopplung
Die Auswahlregeln gelten auch bei den Zeeman-aufgespaltenen
Linien. Die Dipol-Auswahlregeln (siehe Abschnitt 6.7)
erlauben nur
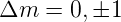 | (6.68) |
Experimentell findet man, dass von allen Elementen nur Ca
und Yb den normalen Zeeman-Effekt zeigen. Alle anderen
Atome zeigen den anomalen Zeeman-Effekt. Bei diesem muss
der Spin des Elektrons mit berücksichtigt werden. Die
dazugehörige Schrödingerleichung, die Pauli-Gleichung,
lautet
![[ ]
^H ψ = --1- (^p + eA )2 + V (r) + -e-^s·B ψ = iℏ ∂-ψ
B,a 2me me ∂t](ap-20181184x.png) | (6.69) |
Wird die Spin-Bahn-Kopplung auch noch berücksichtigt,
bekommt man
![^H ψ
B[,a,sb ]
--1- 2 e-- μ0Ze2--^ -∂-
= 2me (^p + eA ) + V (r ) + me ^s·B + 8πm2er3ℓ·^s ψ = iℏ∂t ψ](ap-20181185x.png) |
(6.70)
|
Aus dieser Gleichung folgt, ohne Rechnung, dass die
Energieeigenwerte
sind. Dabei ist
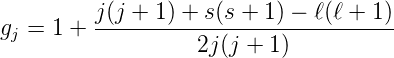
der in (6.56) definierte Landé-Faktor.
6.5.4 Paschen-Back-Effekt
Bei der Spektroskopie von Atomen in hohen Magnetfeldern
spricht man vom Paschen-Back-Effekt. Dieser tritt auf,
wenn die Feinstrukturaufspaltung durch die Kopplung von
magnetischen Spinmomenten mit Bahndrehimpulsmomenten
nicht mehr wesentlich grösser ist als die Kopplung der Spins
oder der Bahndrehmomente an das externe Magnetfeld.
Durch das hohe Magnetfeld wird die Spin-Bahn-Kopplung
aufgelöst, das heisst 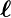 und
und 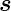 koppeln nicht mehr. Der
Gesamtdrehimpuls
koppeln nicht mehr. Der
Gesamtdrehimpuls 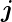 existiert nicht mehr. Das Spektrum
vereinfacht sich. Was bleibt ist die Magnetfeldaufspaltung.
Die magnetische Zusatzenergie ist nun
existiert nicht mehr. Das Spektrum
vereinfacht sich. Was bleibt ist die Magnetfeldaufspaltung.
Die magnetische Zusatzenergie ist nun
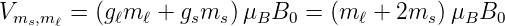 | (6.72) |
Beachten Sie, dass der Faktor 2 vor der Spinkomponente der
g-Faktor ist (keine Quantenfeldtheorie). Die Energieaufspaltung
ist
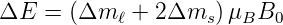 | (6.73) |
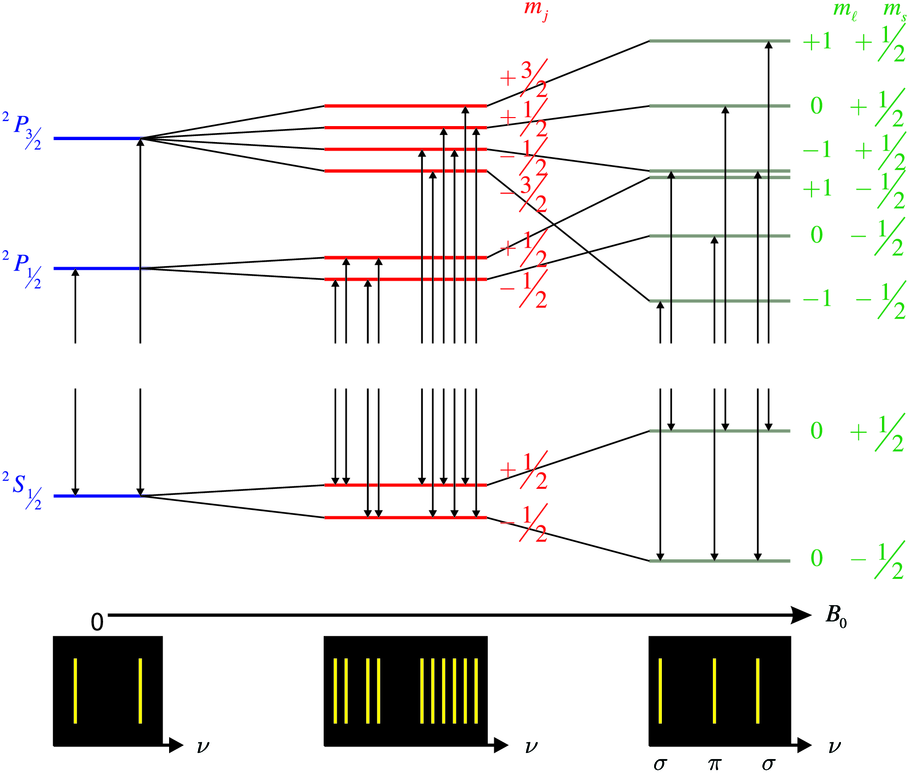
Abbildung 6.5.4 gibt eine Skizze der Elektronenniveaus der
Natrium-D-Linien.
__________________________________________________________________________
Paschen-Back-Effekt bei starken Magnetfeldern.
_____________________________________________________________________
[Nächste Seite] [Vorherige Seite] [vorheriges Seitenende]
[Seitenanfang] [Ebene nach oben]
©2005-2018 Ulm
University, Othmar Marti,  Lizenzinformationen
Lizenzinformationen
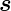 bezeichnet wird. Aus den klassischen
Überlegungen kann aus dem Drehimpuls das magnetische
Moment berechnet werden. Dieses so berechnete Moment ist
jedoch nicht gleich dem gemessenen magnetischen Moment –
ein Zeichen, dass hier die klassische Mechanik die Physik nicht
mehr richtig beschreibt.
bezeichnet wird. Aus den klassischen
Überlegungen kann aus dem Drehimpuls das magnetische
Moment berechnet werden. Dieses so berechnete Moment ist
jedoch nicht gleich dem gemessenen magnetischen Moment –
ein Zeichen, dass hier die klassische Mechanik die Physik nicht
mehr richtig beschreibt.

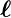 haben wir
haben wir
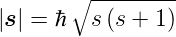
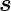
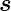
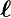 und dem dazugehörigen magnetischen Moment
und dem dazugehörigen magnetischen Moment 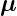
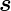 und dessen magnetischem
Moment
und dessen magnetischem
Moment 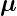
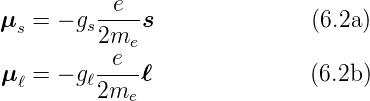
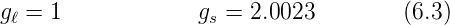
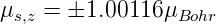
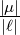 . Das
gyromagnetische Verhältnis für den Bahndrehimpuls und den
Spin ist
. Das
gyromagnetische Verhältnis für den Bahndrehimpuls und den
Spin ist
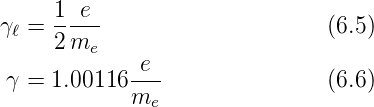
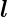 und der Spin
und der Spin 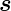 bilden zusammen den
bilden zusammen den
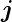 .
.
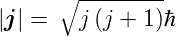
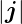
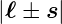 .
.
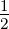 .
.
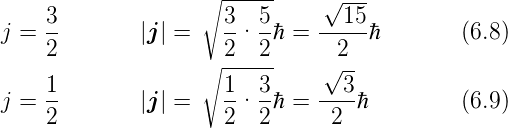
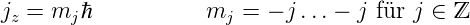
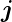 ein magnetisches Moment
ein magnetisches Moment 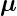
![B ℓ = + Ze-μ0 [v × (− r)] = − Ze-μ0v × r
4πr3 4πr3](ap-20181017x.png)
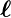
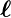
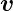
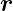 verwendet wurde.
Also ist das Magnetfeld
verwendet wurde.
Also ist das Magnetfeld
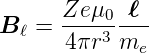
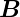
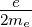
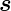 . Setzt man dies in die Gleichung für
die Lageenergie eines magnetischen Moments in einer
magnetischen Induktion
. Setzt man dies in die Gleichung für
die Lageenergie eines magnetischen Moments in einer
magnetischen Induktion 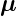
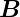 ein, erhält man
ein, erhält man
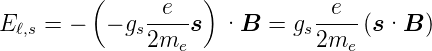
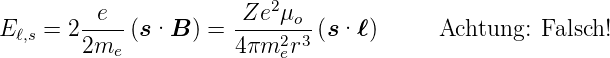
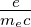
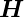 (SI:
(SI: 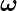
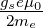
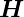 ). Das Elektron bewegt sich mit der
Geschwindigkeit
). Das Elektron bewegt sich mit der
Geschwindigkeit 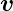 durch die elektrische Verschiebung
durch die elektrische Verschiebung
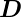
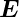 des Kerns, was nach Maxwell zu einem Magnetfeld
des Kerns, was nach Maxwell zu einem Magnetfeld

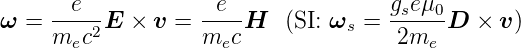
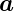 . Man muss eine Lorentz-Transformation
mit der Geschwindigkeit
. Man muss eine Lorentz-Transformation
mit der Geschwindigkeit 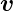
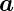
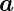
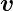
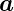
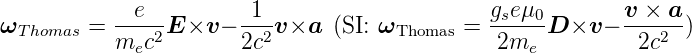
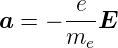
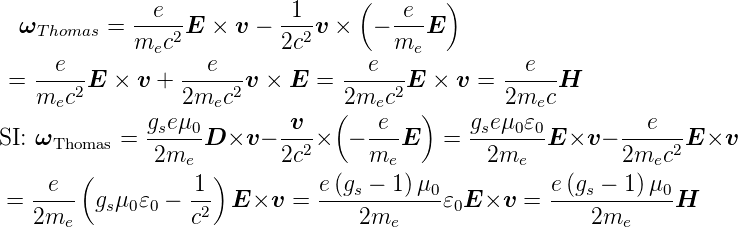
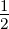 , dem aus der relativistischen Betrachtung
folgenden Thomasfaktor korrigiert werden muss. Wir haben
also für die Energie
, dem aus der relativistischen Betrachtung
folgenden Thomasfaktor korrigiert werden muss. Wir haben
also für die Energie
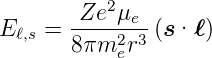
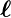
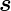
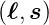
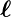
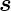
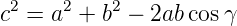
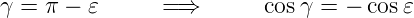
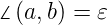
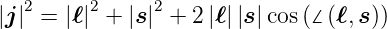
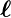 und
und 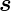 kann also auch
kann also auch
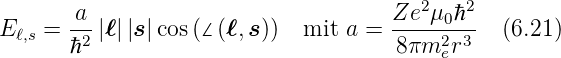
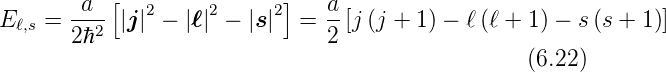
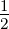 und
und 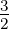 oder
oder
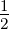 , erhält man die in der Abbildung
, erhält man die in der Abbildung 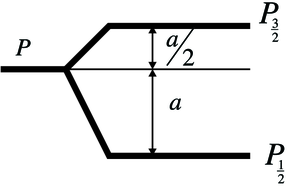
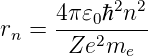
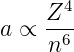
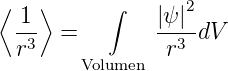
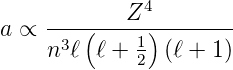
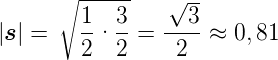
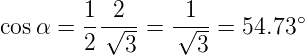
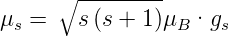
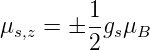
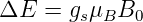
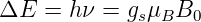
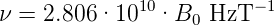
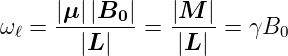
 -Feld kann in drei Komponenten aufgeteilt werden.
Diese drei Polarisationskomponenten ergeben wieder
die ursprüngliche elektromagnetische Schwingung. Die
Polarisationskomponenten sind in Abbildung
-Feld kann in drei Komponenten aufgeteilt werden.
Diese drei Polarisationskomponenten ergeben wieder
die ursprüngliche elektromagnetische Schwingung. Die
Polarisationskomponenten sind in Abbildung 
 beeinflusst die lineare
Schwingung nicht. Die zirkularen Schwingungen (linkszirkular)
und (rechtszirkular) beschleunigen oder bremsen die
Umlauffrequenz der Elektronen auf ihren Bahnen. Die
Frequenzänderung wird die
beeinflusst die lineare
Schwingung nicht. Die zirkularen Schwingungen (linkszirkular)
und (rechtszirkular) beschleunigen oder bremsen die
Umlauffrequenz der Elektronen auf ihren Bahnen. Die
Frequenzänderung wird die 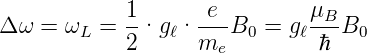
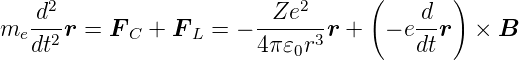
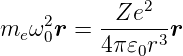
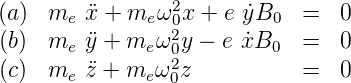
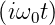 nicht von der magnetischen Induktion
nicht von der magnetischen Induktion
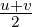 und
und 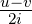 und erhalten aus Gleichung
(
und erhalten aus Gleichung
(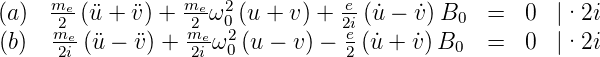
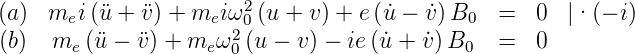
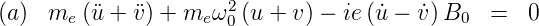
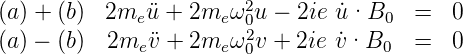
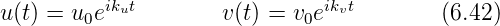
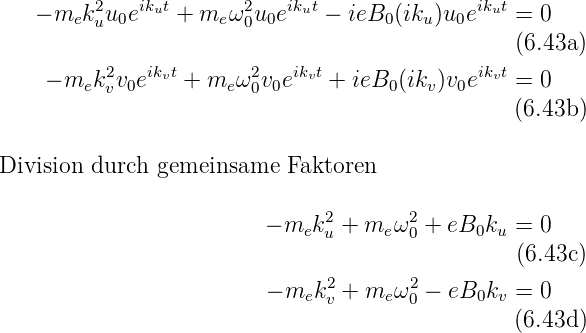
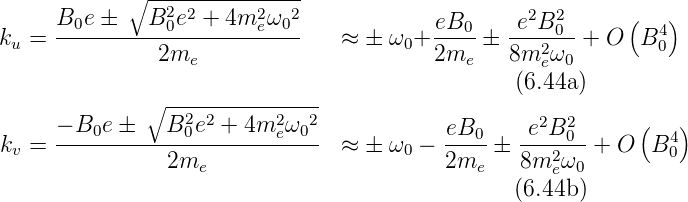
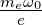 ist, dann sind die Lösungen dieser
Gleichungssysteme
ist, dann sind die Lösungen dieser
Gleichungssysteme 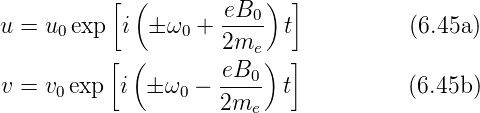
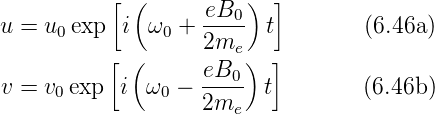
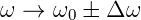
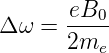
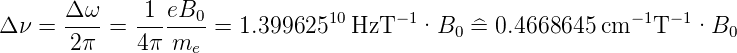
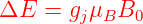

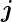 ist parallel zur externen
magnetischen Induktion
ist parallel zur externen
magnetischen Induktion 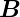 . Da die Präzessionsfrequenz enorm
hoch ist, kann durch eine Messung nur die Projektion von
. Da die Präzessionsfrequenz enorm
hoch ist, kann durch eine Messung nur die Projektion von 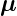
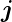 bestimmt werden,
bestimmt werden, 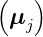
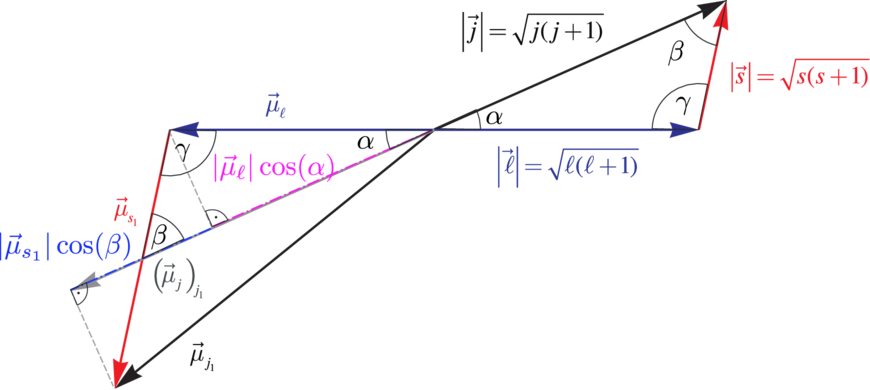
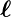
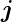
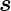
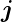
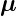
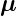
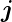 . Wir
können für die Länge des gesamten projizierten magnetischen
Moments
. Wir
können für die Länge des gesamten projizierten magnetischen
Moments 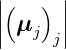 schreiben
schreiben
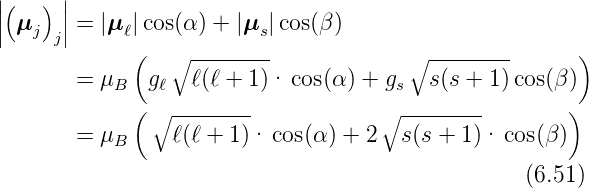
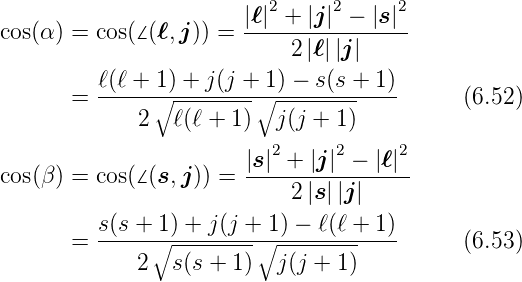
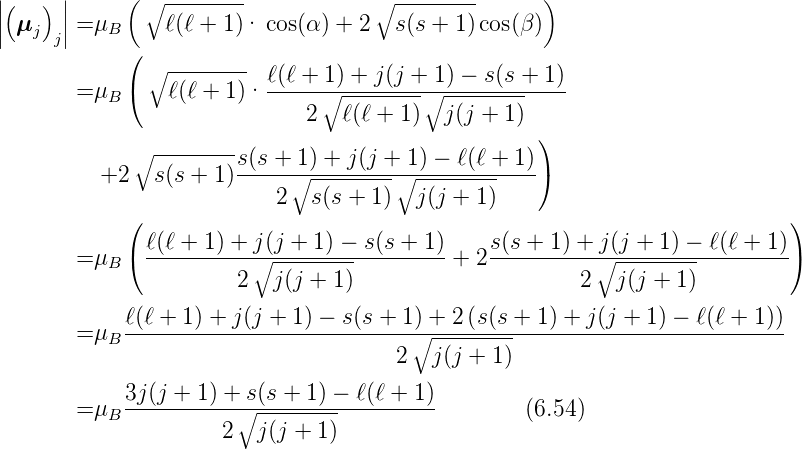
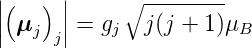
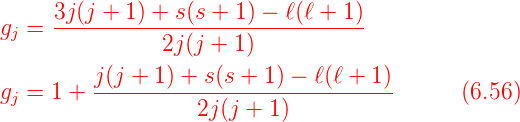
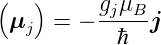
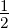
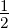
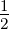
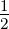
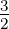
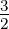
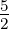
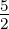
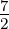
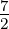
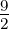
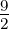
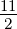
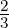
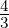
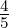
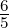
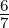
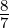
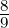
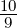
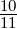
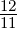
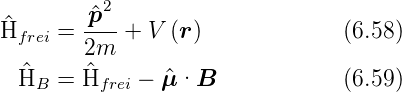
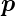
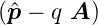
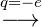
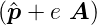 und
und
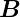

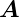
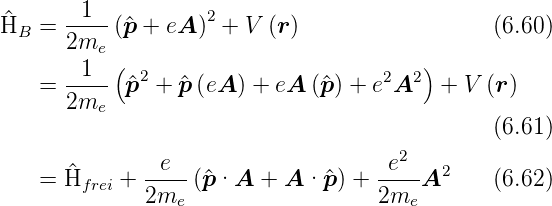
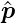
 ein, erhalten wir
ein, erhalten wir
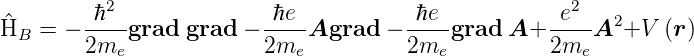
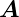 kurz für
kurz für 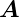
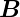
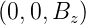 ,
ist ein mögliches Vektorpotential
,
ist ein mögliches Vektorpotential
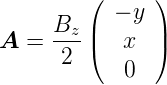
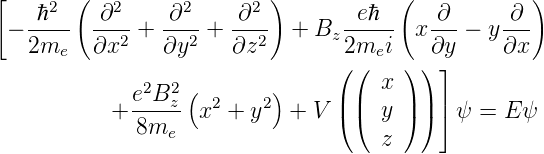
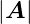
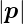 ,
kann der Term mit
,
kann der Term mit 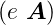
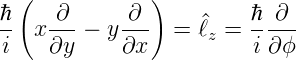
![[ ( ( ) ( ))
ℏ2 1 ∂ 2 ∂ 1 ∂2 1 ∂ ∂
− ---- -2 --- r --- + -2---2----2 + -2-------- sin 𝜃---
2me r ∂r ∂r r sin 𝜃∂ ϕ r ]sin 𝜃∂ 𝜃 ∂ 𝜃
eBz- ℏ-∂-
+ 2m i∂ϕ + V (r) ψ = E ψ
e](ap-20181180x.png)
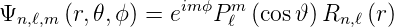
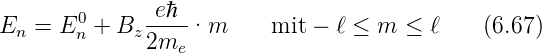
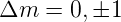
![[ ]
^H ψ = --1- (^p + eA )2 + V (r) + -e-^s·B ψ = iℏ ∂-ψ
B,a 2me me ∂t](ap-20181184x.png)
![^H ψ
B[,a,sb ]
--1- 2 e-- μ0Ze2--^ -∂-
= 2me (^p + eA ) + V (r ) + me ^s·B + 8πm2er3ℓ·^s ψ = iℏ∂t ψ](ap-20181185x.png)
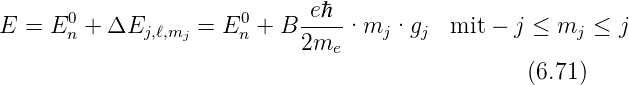
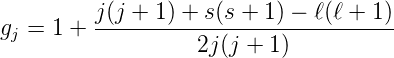
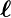 und
und 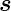 koppeln nicht mehr. Der
koppeln nicht mehr. Der
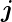 existiert nicht mehr. Das Spektrum
vereinfacht sich. Was bleibt ist die Magnetfeldaufspaltung.
Die magnetische Zusatzenergie ist nun
existiert nicht mehr. Das Spektrum
vereinfacht sich. Was bleibt ist die Magnetfeldaufspaltung.
Die magnetische Zusatzenergie ist nun
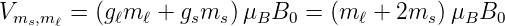
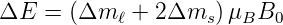
 Lizenzinformationen
Lizenzinformationen