__________________________________________________________________________
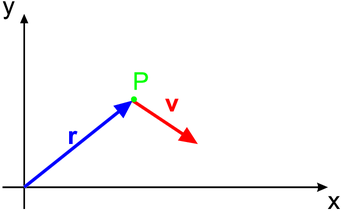
Definition von Vektoren. 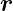 ist ein Ortsvektor,
ist ein Ortsvektor, 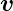 der
Geschwindigkeitsvektor.
der
Geschwindigkeitsvektor.
_____________________________________________________________________

beschreiben Orte oder gerichtete Grössen
__________________________________________________________________________

Definition von Vektoren. 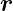 ist ein Ortsvektor,
ist ein Ortsvektor, 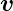 der
Geschwindigkeitsvektor.
der
Geschwindigkeitsvektor.
_____________________________________________________________________
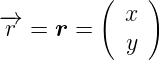
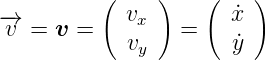
Die Ableitung nach der Zeit wird auch als
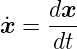
geschrieben.
Addition:
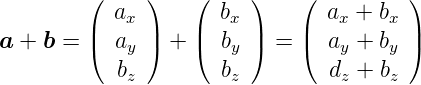 | (D.1) |
| Versuch zur Vorlesung: | |
| Kraft-Polygon (Versuchskarte M-28) | |
Länge eines Vektors
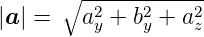 | (D.2) |
Skalarprodukt
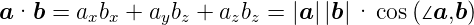 | (D.3) |
der Einheitsvektor 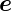 x ist ein Vektor der Länge 1, der in die
x-Richtung zeigt.
x ist ein Vektor der Länge 1, der in die
x-Richtung zeigt.
Vektorprodukt
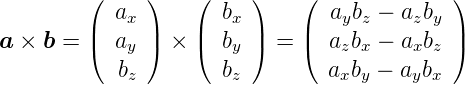 | (D.4) |
Für die Orientierung der Vektoren gilt:
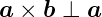 | (D.5) |
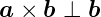 | (D.6) |
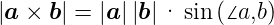 | (D.7) |
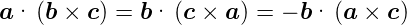 | (D.8) |
Das Spatprodukt berechnet das Volumen des durch 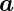 ,
,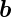 ,
,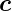 aufgespannten Spates.
aufgespannten Spates.
Gegeben seien zwei Vektoren 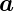 und
und 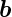 . Die Projektion von
. Die Projektion von 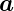 auf
auf 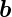 , das heisst, die Komponente von
, das heisst, die Komponente von 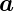 in die Richtung von
in die Richtung von
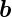 ist
ist
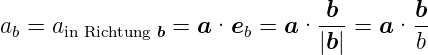 | (D.9) |
In kartesischen Koordinaten heisst dies
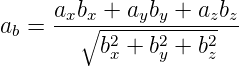 | (D.10) |
Beispiel:
Sei 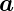 =
= 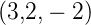 und
und 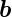 =
= 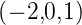 . Dann ist
. Dann ist
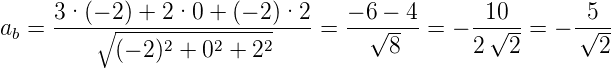 |
Beispiel:
Sei 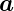 =
= 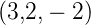 und
und 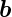 =
= 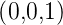 . Dann ist
. Dann ist
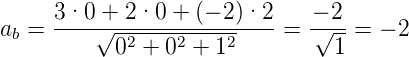 |
Dis ist die z-Komponente von 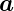 .
.
 Lizenzinformationen
Lizenzinformationen