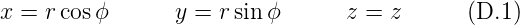

Diese Operatoren können in [AW95] nachgeschaut werden oder mit [WR14] berechnet werden.
Die Definition lautet
Die Skalenfaktoren lauten
Dann ist der Gradient der skalaren Funktion Ψ(r,ϕ,z)
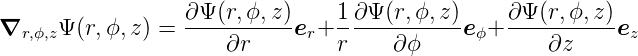 | (D.3) |
Die Divergenz der Vektorfunktion 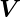 (r,ϕ,z) =
(r,ϕ,z) = 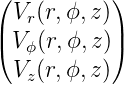 ist
ist
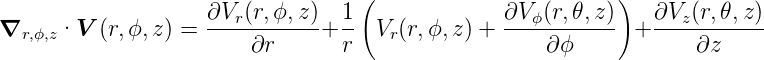 | (D.4) |
Die Rotation der Vektorfunktion 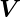 (r,ϕ,z) =
(r,ϕ,z) = 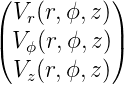 ist
ist
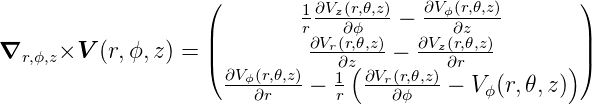 | (D.5) |
Schliesslich lautet der Laplace-Operator der skalaren Funktion Ψ(r,ϕ,z)
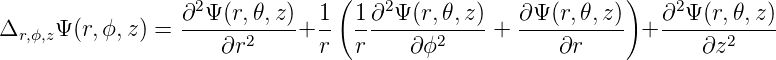 | (D.6) |
Die Definition lautet
Die Skalenfaktoren lauten
Dann ist der Gradient der skalaren Funktion Ψ(r,ϕ,z)
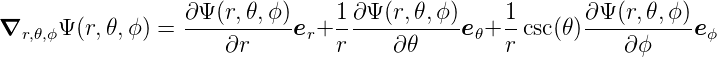 | (D.9) |
Die Divergenz der Vektorfunktion 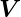 (r,ϕ,z) =
(r,ϕ,z) = 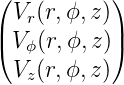 ist
ist
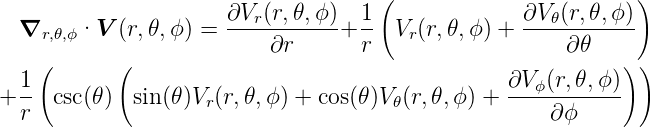 | (D.10) |
Die Rotation der Vektorfunktion 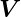 (r,ϕ,z) =
(r,ϕ,z) = 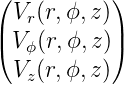 ist
ist
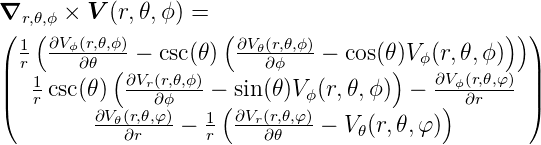 | (D.11) |
Schliesslich lautet der Laplace-Operator der skalaren Funktion Ψ(r,ϕ,z)
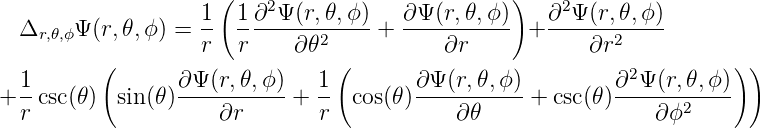 | (D.12) |
 Lizenzinformationen
Lizenzinformationen