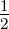E.1  Lagrangefunktion

Die folgenden Ausführungen sind inspiriert vom Buch von Taylor[Tay14]. Wir nehmen an, dass es in einer Dimension eine kinetische Energie: T(v) = 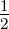mv² und eine potentielle Energie V (x) gibt. Dann definiert man die Lagrange-Funktion

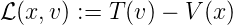(E.1)

Die Ableitungen der Lagrange-Funktion aus Gleichung (E.1) sind

Nach Newton lautet die Bewegungsgleichung

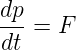(E.3)

Diese kann als Ableitung der Lagrange-Funktion geschrieben werden:

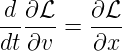(E.4)

Wenn wir die Geschwindigkeit oder die zeitliche Ableitung des Ortes als Variable begreifen, können wir ẋ = v in Gleichungen verwenden. Dann darf nicht nach der Kettenregel nach ẋ abgeleitet werden. Üblicherweise wird die Lagrangefunktion L(x,ẋ) so geschrieben:

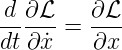(E.5)

Wenn sich nun ein Teilchen unter dem Einfluss des Potential V (x) bewegt, ist die realisierte Bahn ist die, für die die Wirkung S stationär oder extremal ist, also die Variation

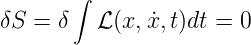(E.6)

gleich null ist.

Das oben gesagte gilt analog auch für mehr Dimensionen und für nicht-kartesische Koordinatensysteme.

Die n Bewegungsgleichungen lauten dann

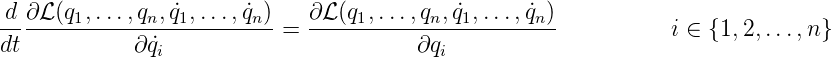(E.8)

E.1.1  Beispiel: Teilchen in 2 Dimensionen in Polarkoordinaten

Für ein Teilchen mit der potentiellen Energie V (r,ϕ) lautet die Lagrange-Funktion:

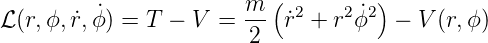(E.9)

Wir betrachten die r- und die ϕ-Komponente getrennt. Die r-Komponente ist

Dise Gleichung kann auch so geschrieben werden:

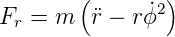(E.11)

−m − r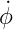² ist dabei die Zentripetalbeschleunigung.

Für die ϕ-Komponente erhalten wir

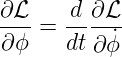(E.12)

oder

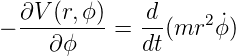(E.13)

Zur Interpretation verwenden wir

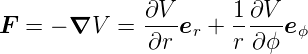(E.14)

und daraus

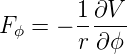(E.15)

Vergleichen wir dies mit der Gleichung (E.13), so können wir schreiben:

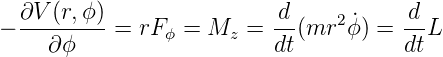(E.16)

Wir sehen also, dass die verallgemeinerte Kraft nichts anderes als das Drehmoment 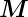ist. Der verallgemeinerter Impuls stellt sich als Drehimpuls 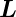heraus.