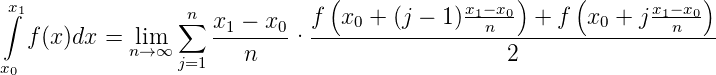

Analog zum Vorgehen bei Ableitungen gehen wir auch bei Integralen vor. Wir verwenden die Definition
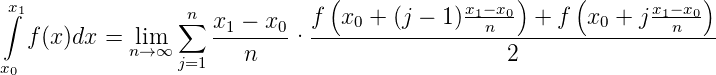 | (I.1) |
In Gleichung (I.1) ist die Trapezregel dargestellt. Alternativ könnte auch mit der Mittelwertregel gearbeitet werden:
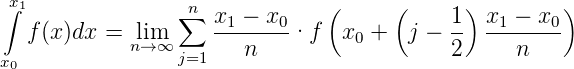 | (I.2) |
Wir können also die beiden Approximationen für das Integral ∫ x0x1f(x)dx angeben:
Wenn man die beiden Approximationen in den Gleichungen (I.3) analysiert, kann die folgende Beziehung abgeleitet werden:
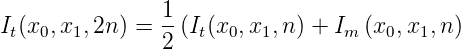 | (I.4) |
Weiter kann man die Grösse
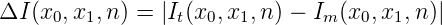 | (I.5) |
als Schätzwert für die Genauigkeit der Approximation verwenden.
Liegt die zu integrierende Funktion nicht als Funktion,
sondern als Tabelle von x-Werten und f(x)-Werten an den
Stellen xj, j ∈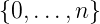 , vor, dann ist das Vorgehen für
einen Schätzwert so:
, vor, dann ist das Vorgehen für
einen Schätzwert so:
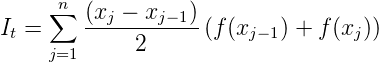 | (I.6) |
Mit den Daten aus Abbildung I.1 und dem Verfahren aus Gleichung I.6 ergibt sich die Tabelle
___________________________________________________________________________
| Originale | Integral | |||
| x | f(x) | x | Int(f(x),0.058,x) | |
| 0.058 | 2.5676 | 0.058 | 0 | |
| 0.2456 | 2.8111 | 0.2456 | 1.009044 | |
| 0.4332 | 3.0546 | 0.4332 | 2.109449 | |
| 0.5693 | 3.348 | 0.5693 | 2.980843 | |
 |  |  |  |
|
| 7.6052 | 6.3168 | 7.6052 | 68.15365 | |
| 7.8576 | 6.4726 | 7.8576 | 71.38169 | |
| 8.1489 | 6.5783 | 8.1489 | 75.18342 | |
 |  |  |  |
|
| 17.2552 | 6.0696 | 17.2552 | 184.8648 | |
| 17.5477 | 6.0867 | 17.5477 | 188.4206 | |
_____________________________________________________________________
In der ersten Zeile der Bezeichnung „Int(f(x),0.058,x)“ steht „0“, in der zweiten Zeile „=(B4+B3)*(A4-A3)+K3“.
__________________________________________________________________________
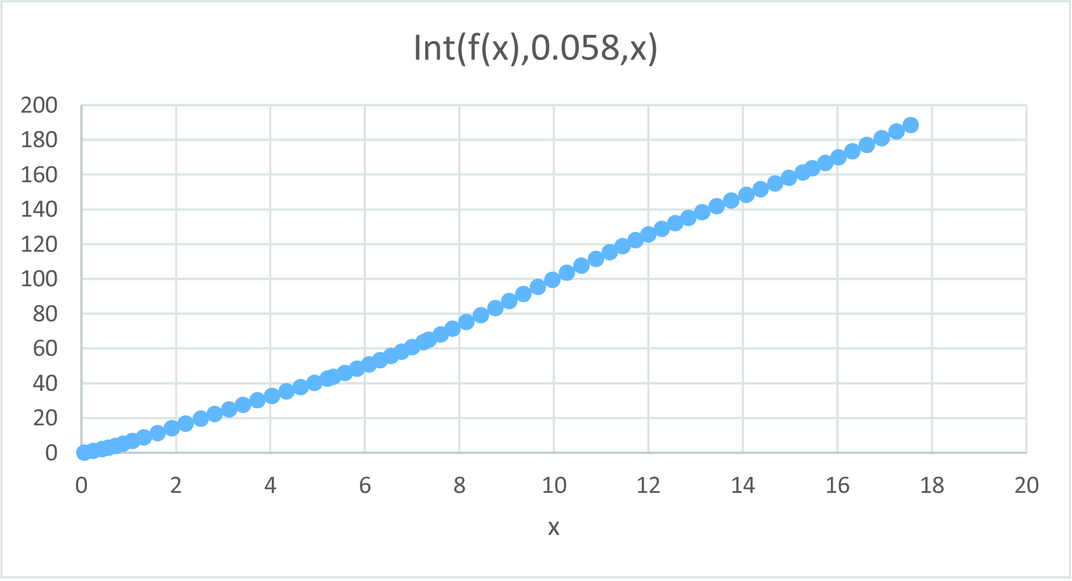
Darstellung der berechneten Integration der Funktion aus Abbildung I.1.
_____________________________________________________________________
In Abbildung I.2 ist die grafische Darstellung der Integration der Funktion aus Abbildung I.1 gezeigt.
Wir wenden hier das Vorgehen aus den Gleichungen (I.3) und (I.4) an.
Die Schätzwerte für das Integral nach der Trapezregel und der Mittenregel können in Mathematica wie folgt definiert werden:
Die Funktion Total summiert über eine Tabelle. Die Funktionen entsprechen den Gleichungen (I.3).
Wir interessieren uns hier für den Verlauf des Fehlers. Dazu werden die Interwalle sukzessive halbiert.
i0 = 0.0981748 ist der nummerische Wert des analytisch berechneten Integrals.
__________________________________________________________________________

Konvergenz der Integralapproximation
_____________________________________________________________________
_____________________________________________________________________
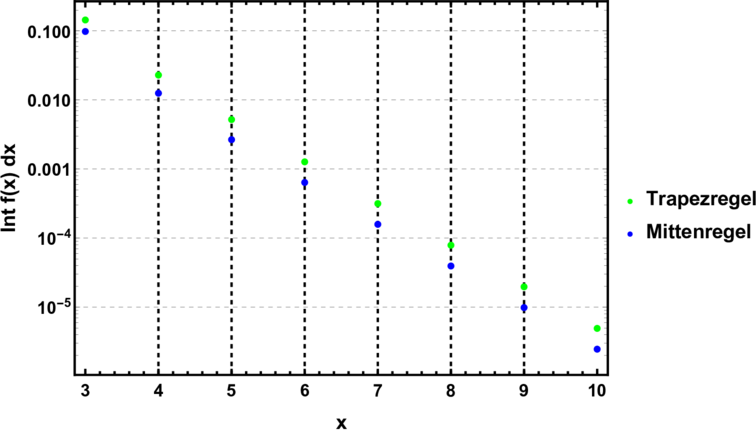
Konvergenz der Integralapproximation (logarithmisch)
_____________________________________________________________________
Die Differenz zwischen Trapezregel und Mittenregel kann als Konvergenzkriterium verwendet werden. Der dazugehörige Mathematica-Code ist:
Wir starten mit 5 Intervallen. Zur Sicherheit wird die maximale Anzahl Iterationen begrenzt. Das Resultat ist
___________________________________________________________________________
| Handgestrickt: | 0.0981756 | aktueller Fehler: | 7.8853·10−7 |
| Iterationen: | 8 | Fehlervorgabe: | 0.00001 |
| Mathematica nummerisch: | 0.0981748 | aktueller Fehler: | 2.22045·10−16 |
| Mathematica symbolisch: | 0.0981748 | ||
_____________________________________________________________________
 Lizenzinformationen
Lizenzinformationen