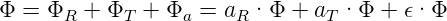

Wärmestrahlung ist eine Form elektromagnetischer Strahlung. Die Sonne versorgt so die Erde mit der notwendigen Energie. Untersucht wurde die Wärmestrahlung um die Jahrhundertwende 1900 vor allem, weil Stahlwerke gerne die Temperatur ihres flüssigen Eisens wissen wollten, zur Prozesssteuerung.
Aus der Optik wissen wir, dass bei einem Strahlungsfluss Φ auf eine Grenzfläche die folgende Energiebilanz gilt:
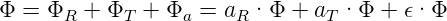 | (3.1) |
wobei ΦT den transmittierten Fluss, ΦR den reflektierten Fluss und Φa den absorbierten Fluss beschreibt. Wir bezeichnen mit 𝜖 den Absorptionsgrad. Nimmt man an, dass die Probe dick ist, gibt es keinen transmittierten Fluss und 𝜖 genügt zur Beschreibung der Wechselwirkung. Da die Gesamtenergie erhalten bleibt, gilt aR = 1 − 𝜖 und damit
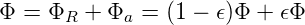 | (3.2) |
Der Absorptionskoeffizienten 𝜖(ν) hängt von der Frequenz der elektromagnetischen Strahlung ab. Wenn dem nicht so wäre, gäbe es zum Beispiel keine Kaltlichtspiegel bei Halogenlampen.
Wenn man die Ausstrahlung einer perfekten schwarzen Fläche (𝜖 = 1, alles einfallende Licht wird perfekt absorbiert) mit Ps beschreibt, ist die Ausstrahlung einer beliebigen Fläche durch
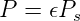 | (3.3) |
gegeben. Dieses Strahlungsgesetz von Kirchhoff bedeutet, dass die Emissionseigenschaften und die Absorptionseigenschaften zusammenhängen. Gut absorbierende Flächen sind auch gut emittierende Flächen. Wenn dem nicht so wäre, könnte man ein Perpetuum Mobile der zweiten Art herstellen.
Nehmen wir an, eine Fläche mit 𝜖1 und der Temperatur T1 strahle die Leistung P1 = 𝜖1Ps(T1) auf die zweite Fläche mit der Temperatur T2. Gleichzeitig strahle die zweite Fläche mit 𝜖2 die Leistung P2 = 𝜖2Ps(T2) auf die erste Fläche. Beide Flächen seien im thermischen Gleichgewicht, das heisst T1 = T2 wenn Ps(T) monoton ist.
Die von der Fläche 1 stammende Leistung P1 wird mit dem Absorptionskoeffizienten 𝜖2 absorbiert. Also ist Pabs,2 = P1𝜖2 und umgekehrt. Im thermischen Gleichgewicht folgt aus T1 = T2
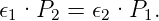 | (3.4) |
Dies ist dann der Fall, wenn die aus der Temperatur berechnete Leistung P(T), die auch nur von der Temperatur abhängt, sich mit Pi wie
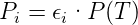 | (3.5) |
verhält. Nur dann ist die Gleichung (3.4) erfüllt.
| Versuch zur Vorlesung: | |
| Pyrometermodell (Versuchskarte AT-12) | |
| Versuch zur Vorlesung: | |
| Infrarotkamera: Optische Temperaturmessung (Versuchskarte AT-44) | |
| Versuch zur Vorlesung: | |
| Wärmestrahlung: Abstandsabhängigkeit bei einer punktförmigen Quelle (Versuchskarte AT-54) | |
(Siehe Gerthsen, Physik [Mes06, pp. 573])
| Versuch zur Vorlesung: | |
| Hohlraumstrahler: Absorption und Emission an Rohr mit Loch (Versuchskarte AT-39) | |
_______________________________________________
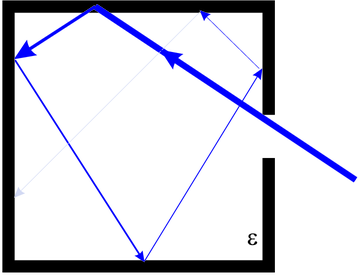

Links: Schematische Darstellung eines schwarzen Körpers. Rechts: Blick auf den Ofen einer Glasbläserei. Die kleine Öffnung wirkt fast wie ein schwarzer Körper.
_____________________________________________________________________
Licht, das durch die kleine Öffnung in den Hohlraum des schwarzen Körpers eintritt, wird bei jeder Reflexion an der Oberfläche mit der Wahrscheinlichkeit 𝜖 absorbiert und mit der Wahrscheinlichkeit 1 − 𝜖 < 1 reflektiert. Nach n Reflexionen ist die verbleibende Intensität des Lichtstrahls auf (1 − 𝜖)n abgesunken, sie wird also beliebig klein. Das heisst, der Absorptionsgrad der Öffnung in diesem Hohlraum ist 𝜖 = 1. Andererseits addieren sich alle emittierten Strahlen auf, so dass die Emission aus der Öffnung identisch ist mit der Emission eines perfekten Schwarzen Strahlers mit 𝜖 = 1.
Spektrale Grössen werden hier mit dem Subskript
ν
 bestimmt. |
Wir definieren nun eine spektrale Energiedichte ϱ(ν,T)dν. Sie besteht aus dem Produkt aus der Energiedichte ϱ(ν,T) und dem Frequenzband der Breite dν, das das Intervall (ν,ν + dν) beschreibt. Diese Energie ϱ(ν,T)dν bewegt sich mit der Geschwindigkeit c durch den Raum und zu den Wänden des Hohlraums. Eine ideale schwarze Wand absorbiert diese Energie ϱ(ν,T) und emittiert nach Kirchhoff gleichzeitig Ps,ν(ν,T). Im Gleichgewicht müssen sich die Absorption und die Emission die Balance halten. Wir können also die spezifische Ausstrahlung durch die Energiedichte ϱ ausdrücken1 .
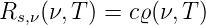 | (3.6) |
oder, integriert über alle Frequenzen,
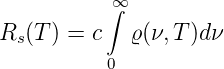 | (3.7) |
Die gemessene spektrale Energiedichte sieht wie in der Abbildung 3.2.2 aus.
__________________________________________________________________________
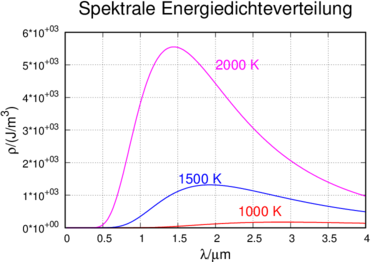
Spektrale Energiedichteverteilung nach Wellenlänge.
_____________________________________________________________________
Wenn man die Energiedichteverteilung gegen die Frequenz aufträgt, erhält man:
__________________________________________________________________________
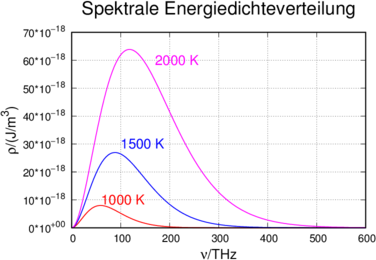
Spektrale Energiedichteverteilung nach Frequenz.
_____________________________________________________________________
| Versuch zur Vorlesung: | |
| Plancksches Strahlungsgesetz: Strahlung einer Glühlampe bei verschiedenen Temperaturen (Versuchskarte AT-21) | |
Im Vorgriff auf das Kommende definieren wir das Plancksches Wirkungsquantum
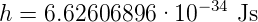 | (3.8) |
Die Grösse können sie sich mit der Eselsbrücke: h ∼ 2π·10−34 Js merken.
Oftmals wird in der Physik, weil es bequemer ist, mit dem reduzierten Wirkungsquantum gerechnet
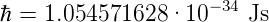 | (3.9) |
Auch hier gibt es eine Eselsbrücke: ℏ = 10−34 Js.
Das Wirkungsquantum ist ein Konzept aus der statistischen Physik, einem Teilgebiet der Thermodynamik.
(Siehe Demtröder, Laserspektroskopie [Dem93, p. 8])
Wir betrachten eine elektromagnetische Welle in einem quaderförmigen Hohlraum. Die Wände des Hohlraumes sollen perfekt leitend sein, das heisst, dass das elektrische Feld auf den Wänden Knotenlinien hat. Der zeit- und ortsabhängige Vektor ihres elektrischen Feldes ist
![∑
E (r,t) = Ei exp[i(ωit + ki·r )] + c.c.
i](ap-201855x.png) | (3.10) |
Dabei muss  i so gewählt werden, dass die Randbedingungen
erfüllt sind.
i so gewählt werden, dass die Randbedingungen
erfüllt sind.
__________________________________________________________________________
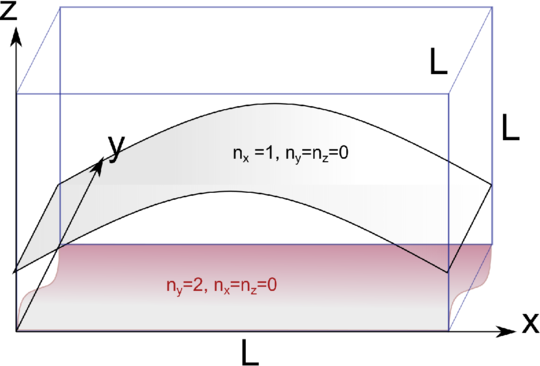
Skizze eines Kastens mit zwei stehenden Wellen. Grau eine Welle mit nx = 1, also der grössten möglichen Wellenlänge, rötlich eine Welle mit einer Knotenlinie im Zentrum, also mit ny = 2.
_____________________________________________________________________
In diesem quaderförmigen Hohlraum (Skizze in Abbildung 3.2.2.1), dessen Quaderseiten entlang den Koordinatenachsen seien, gibt es wegen den Randbedingungen stehende Wellen. Die Wellenzahlen kx, ky und kz sind durch die Ausdehnung in die entsprechende Richtung gegeben. Nur dann wenn eine ganzahlige Anzahl halber Wellenlängen Platz hat, haben wir eine mögliche Welle. Alle Wellen können sowohl in die + wie auch in die −-Richtung laufen. Wir haben also
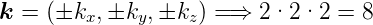 | (3.11) |
mögliche Kombinationen zu einem Tripel (kx,ky,kz). Stehende Wellen erhalten wir nur, wenn die vektoriellen Amplituden der in die + und − Richtung laufenden Wellen gleich sind. Bei einem Würfel mit der Seitenlänge L sind die möglichen Wellenzahlen
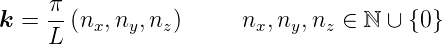 | (3.12) |
Der Betrag der Wellenzahl 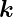 ist
ist
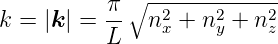 | (3.13) |
Damit gibt es zwischen der Kantenlänge und der Wellenlänge die Beziehung
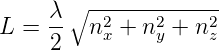 | (3.14) |
Wir wollen nur Wellen bis zu einer maximalen Frequenz
ν = ω∕(2π) betrachten (nach Einstein: mit begrenzter
Energie). Gleichung (3.13) kann mit k = ω∕c umgerechnet
werden (Beachte: sowohl 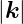 als auch ω geben die Energie der
Welle an, nur in anderen Einheiten!)
als auch ω geben die Energie der
Welle an, nur in anderen Einheiten!)
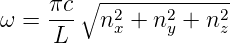 | (3.15) |
Da elektromagnetische Wellen transversal sind, gibt es zwei
Polarisationen entlang den Vektoren 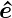 1 und
1 und 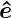 2 (mit
2 (mit 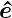 i·
i·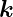 = 0
und
= 0
und 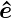 1·
1·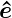 2 = 0). Diese beiden Polarisationsvektoren stehen
senkrecht zum Wellenvektor (der Ausbreitungsrichtung). Das
elektrische Feld der i-ten Mode ist
2 = 0). Diese beiden Polarisationsvektoren stehen
senkrecht zum Wellenvektor (der Ausbreitungsrichtung). Das
elektrische Feld der i-ten Mode ist
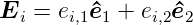 | (3.16) |
Zu jedem einen Wellenvektor beschreibenden Zahlentripel (nx,ny,nz) gibt es zwei Polarisationen. Aus der Linearität der Maxwellgleichungen folgt:
| Jede beliebige Feldkombination im Hohlraum lässt sich als Linearkombination der Moden mit ihren Modenzahlen nx, ny, nz und den beiden Polarisationen darstellen. |
Wir wollen die Anzahl Moden bis zu einer bestimmten oberen Energie bestimmen. Das heisst, dass ω < ωmax oder mit k = ω∕c auch k < kmax sein soll. Die Frage nach der Anzahl Moden ist äquivalent zu:
Wieviele Wellenvektoren mit der Länge 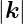 passen in eine
Kugel mit dem Radius kmax? Aus
passen in eine
Kugel mit dem Radius kmax? Aus
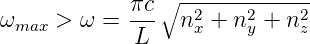 | (3.17) |
folgt
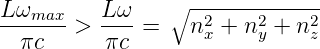 | (3.18) |
Das heisst, dass 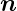 = (nx,ny,nz)T in einer Kugel mit dem
Radius nmax = nR =
= (nx,ny,nz)T in einer Kugel mit dem
Radius nmax = nR = 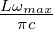 liegt. In dieser Kugel bilden
die möglichen Wellenvektoren ein kubisches Gitter. Der
Frequenzabstand ist Δω =
liegt. In dieser Kugel bilden
die möglichen Wellenvektoren ein kubisches Gitter. Der
Frequenzabstand ist Δω = 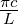 . Dann ist die Gitterkonstante
(Abstand zwischen zwei Netzebenen, siehe auch die
Festkörperphysik) durch Δn =
. Dann ist die Gitterkonstante
(Abstand zwischen zwei Netzebenen, siehe auch die
Festkörperphysik) durch Δn = 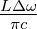 =
= 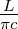
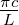 = 1 gegeben. Die
Randeffekte beim Abzählen können vernachlässigt werden,
wenn der Abstand der Gitterpunkte viel kleiner als der
Radius der Kugel ist, also
= 1 gegeben. Die
Randeffekte beim Abzählen können vernachlässigt werden,
wenn der Abstand der Gitterpunkte viel kleiner als der
Radius der Kugel ist, also
 | (3.19) |
ist. Das Volumen einer Kugel ist V = (4π∕3)r3. Da
nx,ny,nz ∈ ℕ∪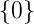 ist, verwenden wir nur 1∕8 des
Kugelvolumens (Siehe auch (3.11)). Die Anzahl Moden bis zu
k =
ist, verwenden wir nur 1∕8 des
Kugelvolumens (Siehe auch (3.11)). Die Anzahl Moden bis zu
k = 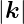 , ω oder n ist
, ω oder n ist
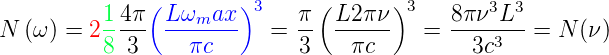 | (3.20) |
wobei die Faktoren die Polarisationen, den Bruchteil des Kugelsegments, und Radius des Kugelsegments darstellen. Die Modendichte erhält man durch Ableiten
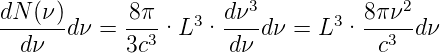 | (3.21) |
Wir erinnern uns, dass wir Moden (stehende Wellen)
in einem würfelförmigen Kasten mit perfekt leitenden
Wänden (Knoten an den Wänden) betrachten. Das
Volumen dieses Kastens ist L3. Analog zur Massendichte
ϱMasse( ) = lim ΔV →0
) = lim ΔV →0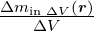 =
= 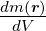 definieren wir die
Modendichte n(ν) = dNin dV (ν)∕dV und erhalten
definieren wir die
Modendichte n(ν) = dNin dV (ν)∕dV und erhalten
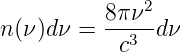 | (3.22) |
Wir kennen nun die Anzahl Moden pro Frequenzintervall, das heisst auch die Modendichte bei der Frequenz ν. Es bleibt die Frage, wie wahrscheinlich ist es, eine Mode bei der Frequenz hν zu finden wenn die Temperatur T ist. Diese Frage muss mit den Methoden der Thermodynamik beantwortet werden [Mar15].
Nach Albert Einstein kann die Energie des Lichtes nur diskrete Werte annehmen, E = hν, und ganzzahlige Vielfache davon, also E(j) = j·hν mit j ∈ℕ. Die Wände unseres Resonators sollen die Temperatur T haben. Das heisst, dass wenn die Eigenschwingungen im thermischen Gleichgewicht mit den Wänden sind, die Statistik der Eigenschwingungen nach Boltzmann auch durch die Temperatur T gegeben sein muss.
Die Wahrscheinlichkeit p(j) pro Volumen und damit dann auch die wahrscheinlichkeitsdichte der Eigenschwingungen mit der Energie W(j) = j·hν im Gleichgewicht mit Wänden der Temperatur T ist nach Boltzmann und der statistischen Thermodynamik
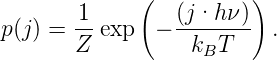 | (3.23) |
Die Grösse Z in dieser Gleichung ist die Zustandssumme
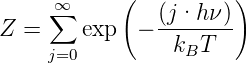 | (3.24) |
Ab hier betrachten wir alle Moden mit allen möglichen Energien. Dabei sind sehr hohe Energien extrem unwahrscheinlich! Mit dieser Definition ist p(j) normiert:
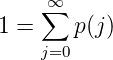
Die mittlere Energiedichte pro Eigenschwingung ergibt sich nun als gewichtete Summe (z.B. wie bei der Berechnung des Trägheitsmomentes bei der Drehung um eine Achse). p(j) ist das Gewicht, gemittelt werden die Energien j·hν.
![∑∞ 1 ∑∞ [ ( (j·h ν)) ]
¯ϱdν = ·p (j)(j·h ν )d ν = -- exp − -------- · (j·h ν) d ν
j=0 Z j=0 kBT](ap-201892x.png) | (3.25) |
Zur Berechnung der Summe verwenden wir dass
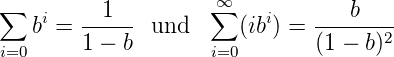
ist. Nach einer Variablentransformation erhalten wir für unsere Gleichungen (3.25) und (3.24)
Indem wir Gleichung (3.26) durch (3.27) teilen, also Gleichung (3.25) betrachten, erhalten wir
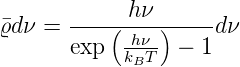 | (3.28) |
Die spektrale Strahlungsdichte ϱ(ν,T) bekommen wir,
indem die mittlere Energiedichte pro Eigenschwingung mit
der Dichte der Eigenschwingungen n(ν) = 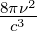 multipliziert
wird. Wir erhalten das Plancksche Strahlungsgesetz.
multipliziert
wird. Wir erhalten das Plancksche Strahlungsgesetz.
Plancksches Strahlungsgesetz
|
Wenn wir das Plancksche Strahlungsgesetz mit Wellenlängen ausdrücken wollen, dann müssen wir die folgenden Substitutionen machen:
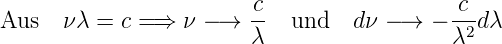 |
Damit wir das Planksche Strahlungsgesetz mit Wellenlängen als unabhängige Variable:
Plancksches Strahlungsgesetz für Wellenlängen
|
Einsteins Quantenhypothese Ausgehend von seinem Verständnis des Fotoeffekts [Ein05] kam Einstein zur folgenden Hypothese:
| Quantenhypothese Einsteins Atome, die die Energie hν absorbieren, haben eine höhere Energie als Atome im Grundzustand. |
Wir verwenden die folgenden Definitionen:
Wir nehmen thermisches Gleichgewicht an und verwenden deshalb die Boltzmann-Verteilung zur Berechnung der Teilchenzahldichte der angeregten Atome
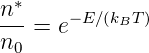 | (3.31) |
Albert Einstein nahm an, dass wie in Abbildung 3.2.2.1.1 dargestellt der Energieaustausch zwischen dem Unteren und dem oberen Zustand auf drei Wegen möglich sei. Die Anregung aus dem unteren Zustand in den oberen Zustand (Niveau) geschieht nur, wenn externe Energie absorbiert wird. Der höherenergetischen Zustand kann auf zwei Wegen verlassen werden: erstens zufällig (statistisch) oder induziert, das heisst im Takt mit externen Feldern.
__________________________________________________________________________
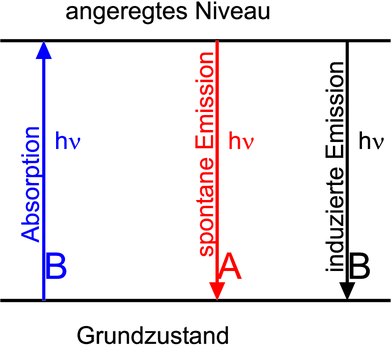
Schema der möglichen Anregungen und Emissionen in einem Zweiniveau-Atom.
_____________________________________________________________________
Einstein hatte als Neuerung die induzierte Emission postuliert. Zur Berechnung des Spektrums eines schwarzen Strahlers verwenden wir die Einsteinsche Formulierung mit Quanten. Ursprünglich hatte Planck das Spektrum mit thermodynamischen Methoden berechnet, wobei h das aus der statistischen Physik bekannte Phasenraumvolumen war. Ein Phasenraumelement ist eine Fläche, deren eine Seite eine Länge und deren andere Seite eine Geschwindigkeit ist.
Die Anzahlen der Absorptionen und Emissionen werden wie folgt angegeben:
wobei A den Einsteinkoeffizienten den spontanen Emission, B1 den Einsteinkoeffizienten der Absorption und B2 den Einsteinkoeffizienten der induzierten Emission bedeutet.
Diese Beziehungen können so verstanden werden:
Von der Einsteinschen Quantenhypothese zum Planckschen Strahlungsgesetz Im Gleichgewicht muss es gleich viele Emissionen wie Absorptionen geben.
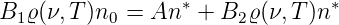 | (3.33) |
Da die induzierte Emission der Umkehrprozess zur Absorption ist, muss
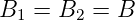 | (3.34) |
sein. Wir können Gleichung (3.33) wie folgt umformen:
![B ϱ(ν,T)n0 = (A + B ϱ(ν,T)) n∗ = [A + B ϱ(ν,T )]n0e −E∕(kBT )](ap-2018104x.png) | (3.35) |
Damit erhalten wir die Energiedichte
![[ −E ∕(k T)] −E∕(k T)
B ϱ(ν,T )n0 1 − e B = An0e B](ap-2018105x.png)
Infinitesimal geschrieben bekommen wir
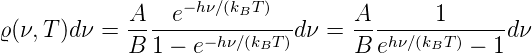 | (3.36) |
Unbekannt ist nun noch A∕B. Durch Vergleich mit der Gleichung (3.29) bekommen wir diesen Koeffizienten (aus der spektralen Energiedichte) des Hohlraumes
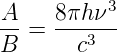 | (3.37) |
Die spektrale Energiedichte ist verknüpft mit der Modendichte und sagt, wie viele Resonanzen es pro Frequenzintervall gibt. Zusammen bekommen wir analog zu Gleichung (3.29) das Plancksche Strahlungsgesetz:
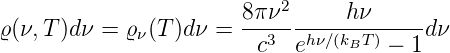 | (3.38) |
Es ist nun instruktiv, die beiden Grenzfälle für sehr hohe und für sehr niedrige Frequenzen zu betrachten. Für sehr niedrige Frequenzen, im Grenzfall hν « kBT, gilt
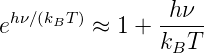
Dies führt auf das Rayleigh-Jeans-Gesetz.
Rayleigh-Jeans-Gesetz
|
Dieses Gesetz war vor Planck bekannt. Es sagt voraus, dass die Energiedichte gegen hohe Frequenzen zunimmt, dass also im Ultravioletten die gesamte unendlich grosse Energie des Universums konzentriert sei. Diese Ultraviolettkathastrophe zeigt, dass das Gesetz nur in Teilbereichen stimmen kann.
Für sehr hohe Frequenzen, also hν » kBT, gilt
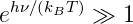
Dann kann das Plancksche Strahlungsgesetz durch das Wiensche Strahlungsgesetz angenähert werden
Wiensches Strahlungsgesetz
|
Das Wiensche Strahlungsgesetz (siehe Abbildung 3.2.2.1.2) stimmt einigermassen, aber doch nicht so korrekt wie das Plancksche Strahlungsgesetz. Insbesondere ergibt sich aber bei Wien keine Ultraviolettkatastrophe.
__________________________________________________________________________
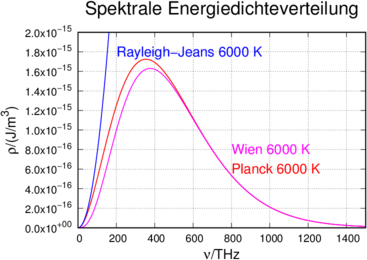
Vergleich der Gesetze von Planck, Wien und Rayleigh-Jeans bei 6000K
_______________________________________________________________
Penzias und Wilson fanden Anfang der sechziger Jahre des zwanzigsten Jahrhunderts, dass das Rauschen höchstempfindlicher Antennen, wenn sie nach oben gerichtet waren, die gleiche Spektralverteilung hatte, wie ein schwarzer Strahler bei etwa 2.7 K. Abbildung 3.2.2.1.2 zeigt die kosmische Energiedichteverteilung
__________________________________________________________________________
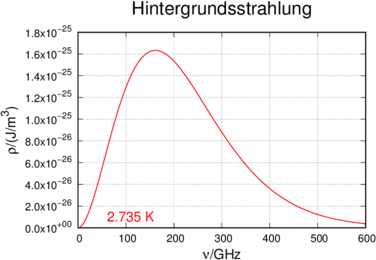
Spektrale Energiedichteverteilung der Hintergrundsstrahlung von 2.735K
_______________________________________________________________
Oftmals möchte man die Frequenz ν wissen, bei der das Emissionsspektrum des schwarzen Strahlers maximal ist. Zur Berechnung des Maximums substituieren wir in Gleichung (3.29)
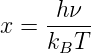
und setzen
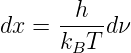
Weiter vernachlässigen wir die konstanten Vorfaktoren, die für die Lage des Maximums irrelevant sind. Wir erhalten
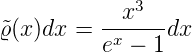 | (3.41) |
Durch Ableiten erhalten wir die Lage des Maximums
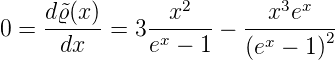
Vereinfacht ergibt sich
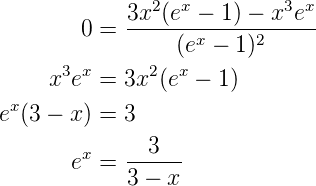
Die Lösung dieser transzendenten Gleichung ist
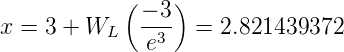
wobei WL Lamberts W-Funktion ist. Also kann die Lage des Maximums in der Planckschen Strahlungsformel (3.29) durch das Wiensche Verschiebungsgesetz angegeben werden.
Wiensches Verschiebungsgesetz
|
Die folgende Abbildung 3.2.2.2 zeigt eine graphische Darstellung des Wienschen Verschiebungsgesetzes.
__________________________________________________________________________
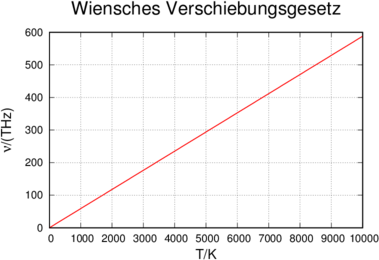
Wiensches Verschiebungsgesetz
_____________________________________________________________________
Die Energiedichte beim Emissionsmaximum des Wienschen Verschiebungsgesetzes ist
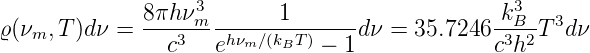 | (3.43) |
Abbildung 3.2.2.2 stellt Gleichung (3.43) graphisch dar.
__________________________________________________________________________
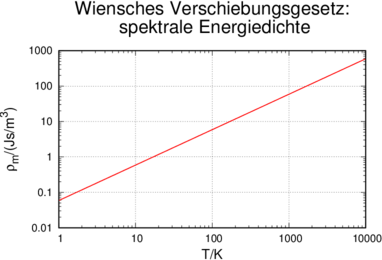
Energiedichte im spektralen Maximum nach dem Wienschen Verschiebungsgesetz
_____________________________________________________________________
Möchte man die Wellenlänge λm des Maximums des Planckschen Spektrums eines schwarzen Strahlers wissen, substituieren wir in Gleichung (3.30)
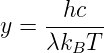
und setzen
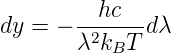
Weiter vernachlässigen wir die konstanten Vorfaktoren, die für die Lage des Maximums irrelevant sind. Wir erhalten
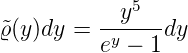 | (3.44) |
Durch Ableiten erhalten wir die Lage des Maximums
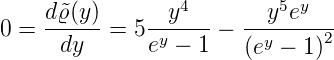
Vereinfacht ergibt sich
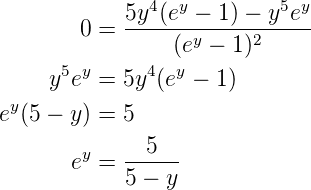
Die Lösung dieser transzendenten Gleichung ist
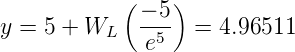
wobei WL Lamberts W-Funktion ist. Also kann die Lage des Maximums in der Planckschen Strahlungsformel (3.30) durch das Wiensche Verschiebungsgesetz angegeben werden.
Wiensches Verschiebungsgesetz für Wellenlängen
|
| Versuch zur Vorlesung: | |
| Strahlungswürfel nach Leslie: Emissionsfaktor von verschiedenen Strahlern (Versuchskarte AT-20) | |
| Versuch zur Vorlesung: | |
| Stefan-Boltzmannsches Gesetz: mit Leslie-Würfel (Versuchskarte AT-43) | |
Wir möchten wissen, wie die Abstrahlung eines schwarzen Körpers von dessen Temperatur abhängt. Dazu definieren wir zunächst die spezifische Ausstrahlung nach Gleichung (3.6) senkrecht zur Oberfläche
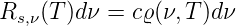 | (3.46) |
Daraus bekommen wir die richtungsabhängige Abstrahlung (𝜃 ist der Winkel zur Normalen)
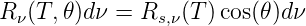 | (3.47) |
Diese Grösse ist sowohl von der Frequenz wie auch von der Richtung abhängig. Der Mittelwert einer allgemeinen richtungsabhängigen Grösse f(𝜃,ϕ) ist
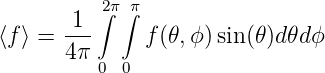 | (3.48) |
Über den Halbraum gerechnet erhalten wir (unter der Voraussetzung, dass f(𝜃,ϕ) = f(π − 𝜃,ϕ) ist)
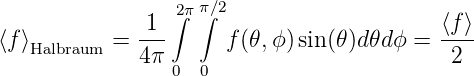 | (3.49) |
Zusammen mit der Mittelung über die Frequenz erhalten wir
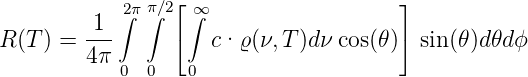 | (3.50) |
Diese drei Integrale sind voneinander unabhängig. Wir beachten, dass
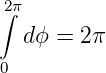
und
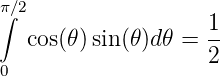
ist und erhalten
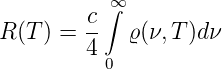 | (3.51) |
Mit Gleichung (3.29) ergibt dieses Integral
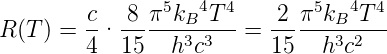 | (3.52) |
Wir definieren die Stefan-Boltzmann-Konstante
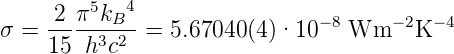 | (3.53) |
und können dann das Stefan-Boltzmann-Gesetz so formulieren:
Stefan-Boltzmann-Gesetz
|
R ist die in den Halbraum abgestrahlte Leistung bei der Temperatur T. Diese Leistung R(T) ist in der Abbildung 3.2.2.4 in doppelt-logarithmischer Darstellung gezeichnet.
__________________________________________________________________________
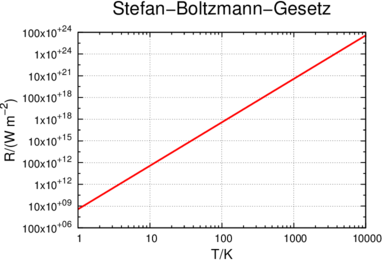
Stefan-Boltzmann-Gesetz
_____________________________________________________________________
__________________________________________________________________________
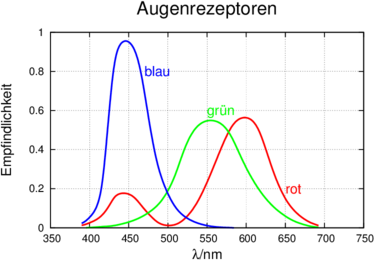
Empfindlichkeitskurven der Augenrezeptoren skaliert auf gleiche integrale Empfindlichkeit (nach [Mes06])
_____________________________________________________________________
Was wir Farben nennen, hängt von der Interpretation der Reize unserer Sehnerven ab. Abbildung 3.2.3 zeigt die spektrale Empfindlichkeit des Auges.
__________________________________________________________________________
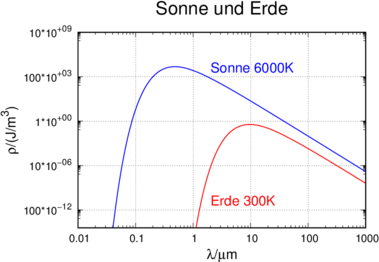
Vergleich der spektralen Energiedichte von Sonne und Erde. Die verschiedene Lage der Maxima ermöglicht den Treibhauseffekt.
_____________________________________________________________________
Sowohl die Sonne wie auch die Erde können in guter Näherung durch schwarze Strahler approximiert werden. Abbildung 3.2.4 zeigt die beiden Kurven, wobei die Erde die Temperatur 300 K und die Sonne die Temperatur 6000 K hat. Die Unterschiede der beiden Kurven bewirken, dass die Energiezufuhr zur Erde bei einer anderen Wellenlänge oder Frequenz geschieht wie deren Abstrahlung.
 Lizenzinformationen
Lizenzinformationen