Weiter: Schaltungen und Bauelemente Oben: Elektrische Ströme Zurück: Elektromotorische Kraft und Joulsche Skript: PDF-Datei Übungen: Blätter
(Siehe Leisi, Klassische Physik II [Lei98, pp. 88]) (Siehe Tipler, Physik [TM04, pp. 761]) (Siehe Tipler, Physik [TM04, pp. 790])
|
|
Ohne ein Verständnis von Stromkreisen sind moderne elektronische Schaltungen nicht verständlich. Wir betrachten deshalb Schaltungen aus Kondensatoren und Widerständen. Zur Erinnerung: die relevanten Gleichungen sind
Wir betrachten die folgende Schaltung
![\includegraphics[width=0.6\textwidth]{strom-001}](img661.gif)
Aufladen und Entladen eines Kondensators über einen Widerstand.
|
Für die Zeit ![]() soll der Schalter
soll der Schalter ![]() in der gezeigten Stellung sein. Die Spannung am Kondensator ist
in der gezeigten Stellung sein. Die Spannung am Kondensator ist
![]() . Damit ist auch
. Damit ist auch ![]() und
und ![]() . Für
. Für ![]() wird der Kondensator
wird der Kondensator ![]() mit der Spannungsquelle
mit der Spannungsquelle ![]() verbunden. Da Spannungen im quasistationären Falle sich wie potentielle Energien verhalten, kann man für
verbunden. Da Spannungen im quasistationären Falle sich wie potentielle Energien verhalten, kann man für
| (3.206) |
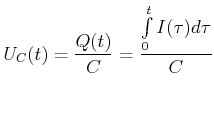 |
(3.207) |
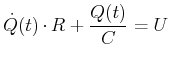 |
(3.208) |
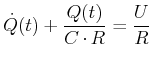 |
(3.209) |
Zur Lösung dieser Differentialgleichung machen wir den Ansatz
| (3.210) |
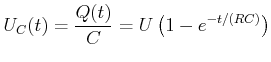 |
(3.211) |
| (3.212) |
![\includegraphics[width=0.7\textwidth]{rc-laden}](img677.gif)
Ladekurven am Kondensator. Die verwendeten Werte sind
|
Die Differentialgleichung für das Entladen lautet
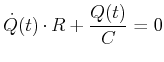 |
(3.213) |
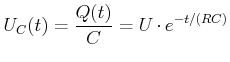 |
(3.214) |
| (3.215) |
![\includegraphics[width=0.7\textwidth]{rc-entladen}](img684.gif)
Entladekurven am Kondensator. Die verwendeten Werte sind
|
Die Grösse
![]() ist die Zeitkonstante der Schaltung. In der Zeit
ist die Zeitkonstante der Schaltung. In der Zeit ![]() steigt
steigt ![]() beim Einschalten
von 0 auf
beim Einschalten
von 0 auf ![]() . Ebenso fällt beim Ausschalten die Spannung in der Zeit
. Ebenso fällt beim Ausschalten die Spannung in der Zeit ![]() von
von ![]() auf
auf ![]() ab.
ab.
Eine alternative Ableitung dieser Gleichung verwendet eine Leistungsbetrachtung. Die Leistung der Joulschen Wärme im Widerstand und die zeitliche Änderung der Energie im Kondensator müssen gleich der von der Batterie gelieferten Leistung sein.
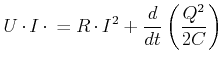 |
(3.216) |
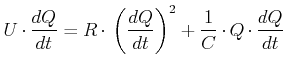 |
(3.217) |
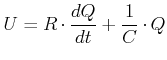 |
(3.218) |
Othmar Marti