Weiter: Innerhalb und ausserhalb einer Oben: Berechnung elektrischer Felder Zurück: In der Nähe eines Skript: PDF-Datei Übungen: Blätter
Zur Berechnung setzen wir die Flächenladungsdichte auf
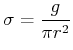
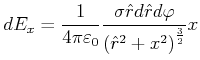
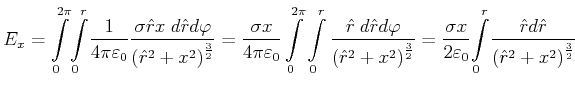
Nach Bronstein ist
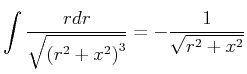
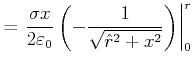 |
||
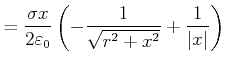 |
||
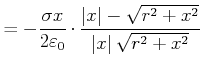 |
||
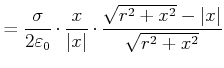 |
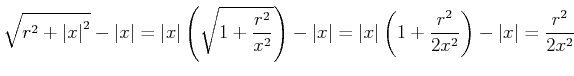
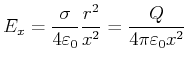
![\includegraphics[width=0.8\textwidth]{kreisladung}](img2257.gif)
|
Othmar Marti