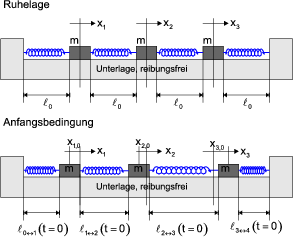
Zur Zeit t = 0 werden die Massen auf die Positionen x1,0, x2,0 und x3,0 ausgelenkt.
- Geben Sie das System der Bewegungsgleichungen an.
- Lösen Sie die Bewegungsgleichungen mit den Methoden aus Abschnitt 8.1.6 „Klassische und relativistische Physik“.
- Welches sind die Eigenschwingungen? Wieviele Eigenschwingungen gibt es?
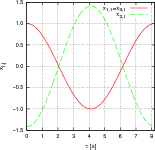
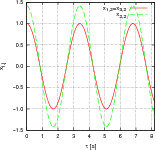
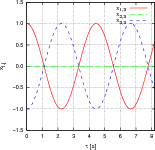
- Skizzieren Sie x1(t), x2(t) und x3(t) für alle Eigenschwingungen.
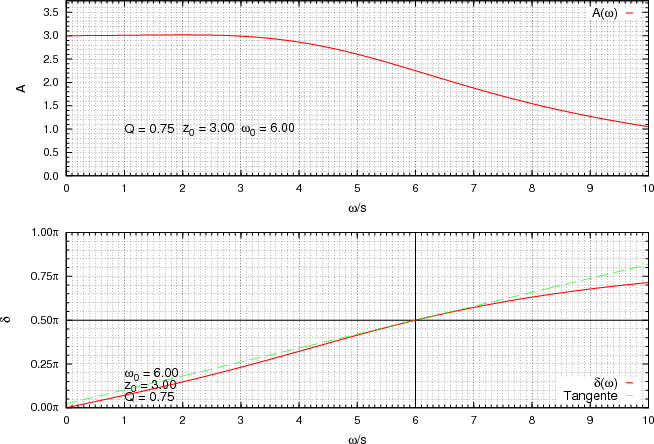
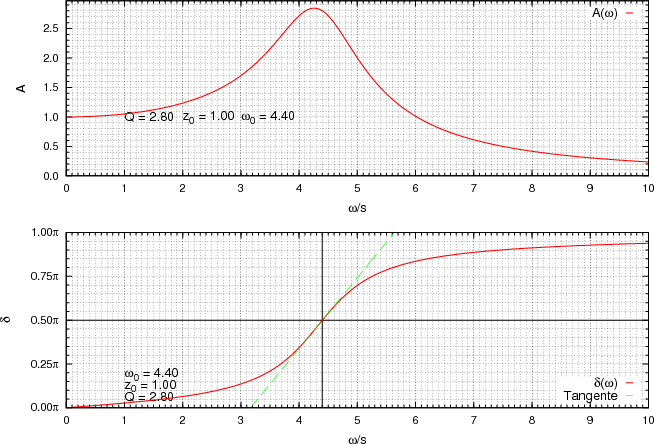
- die Resonanzfrequenz des ungedämpften harmonischen Oszillators ω0
- die Güte Q
- die Amplitude der treibenden Schwingung z0
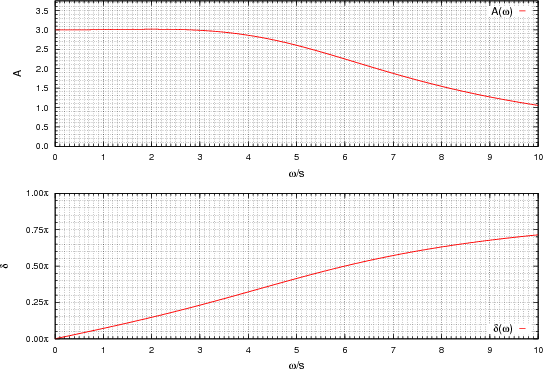
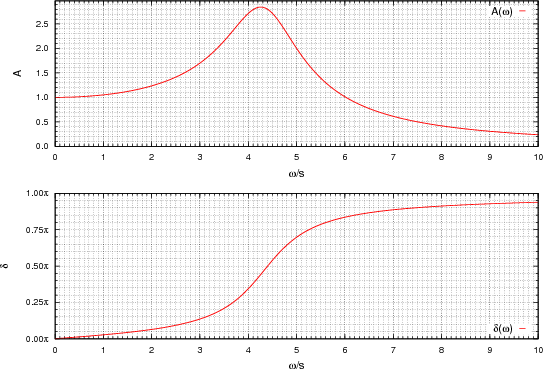
- die Resonanzfrequenz des ungedämpften harmonischen Oszillators ω0
- die Güte Q
- die Amplitude der treibenden Schwingung z0
- Berechnen Sie die Gesamtladung der Erde, die notwendig ist, um eine der Gravitationskraft zwischen Erde und Sonne gleiche anziehende elektrostatische Kraft zu erzeugen.
- Wenn die Ladung eines Elektrons qe = -1.6 ⋅ 10-19 C ist und die Elektronen gleichmässig über die Erdoberfläche verteilt sind, wie gross ist dann die jedem Elektron zustehende Fläche?
- Berechnen Sie entlang der x-Achse die Coulombkraft auf eine Testladung q0.
- Berechnen Sie entlang der y-Achse die Coulombkraft auf eine Testladung q0.
PDF-Version des Aufgabenblattes
Gegeben ist die Schwingungsdifferentialgleichung
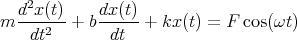
- Wie lautet die homogene Differentialgleichung?
- Lösen Sie die homogene Differentialgleichung unter der Annahme dass b2 > 4mk ist.
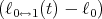
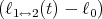
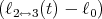
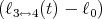
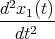
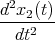
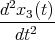
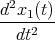
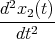
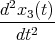
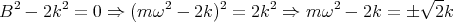
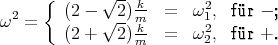
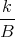
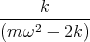
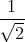
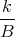
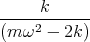
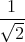
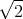
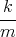
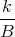
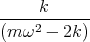
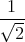
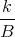
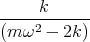
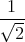
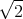
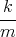
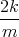
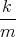
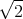
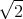
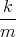
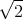
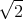
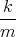
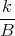
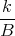
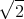
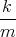
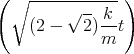
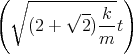
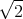
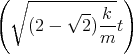
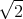
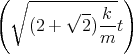
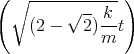
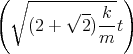
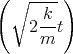
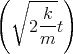
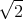
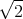
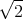
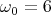
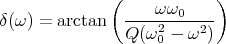
![| [ ]
dδ(ω)|| -------1-------- ----ω0------ -ωω0-(--2ω0)- 2Q-
dω | = ( ω ω0 )2 ⋅ Q (ω2- ω2) - Q (ω2 - ω2 )2 = ω0
ω= ω0 1 + Q(ω20-ω2) 0 0 ω=ω0](uebungsblatt0171x.png)
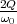
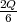
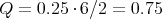
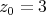
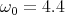
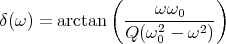
![| [ ]
dδ(ω)|| -------1-------- ----ω0------ -ωω0-(--2ω0)- 2Q-
dω | = (--ω-ω0--)2 ⋅ Q (ω20 - ω2) - Q (ω2 - ω2 )2 = ω0
ω= ω0 1 + Q(ω20-ω2) 0 ω=ω0](uebungsblatt0179x.png)
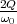
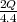
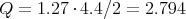
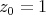
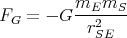
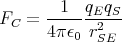
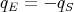
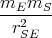
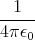
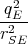
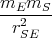
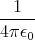
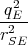
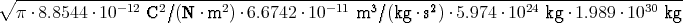
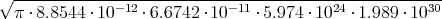
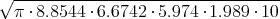
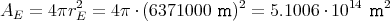
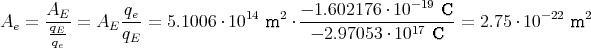
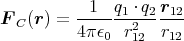
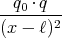
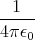
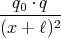
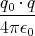
![[ ]
---1---- ---1----
(x - ℓ)2 - (x + ℓ)2](uebungsblatt01105x.png)
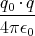
![[ 2 2]
(x-+-ℓ)---(x---ℓ)--
(x2 - ℓ2)2](uebungsblatt01107x.png)
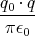
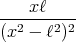
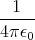
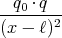
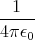
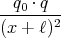
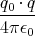
![[ 1 1 ]
-------2 + -------2
(x - ℓ) (x + ℓ)](uebungsblatt01115x.png)
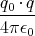
![[ ]
(x +-ℓ)2 +-(x---ℓ)2-
(x2 - ℓ2)2](uebungsblatt01117x.png)
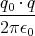
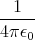
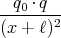
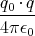
![[ ]
---1---- ---1----
- (x - ℓ)2 + (x + ℓ)2](uebungsblatt01125x.png)
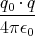
![[ 2 2]
- (x-+-ℓ)-+-(x---ℓ)-
(x2 - ℓ2)2](uebungsblatt01127x.png)
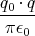
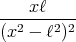
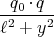
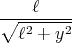
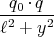
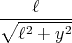
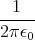
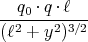
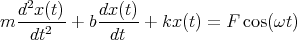
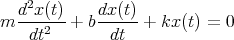
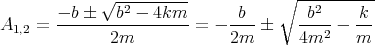
![[ ]
- -bt ∘ -b2---kt - ∘-b2-- kt
x(t) = e 2m x0,+e 4m2 m + x0,- e 4m2 m](uebungsblatt01141x.png)