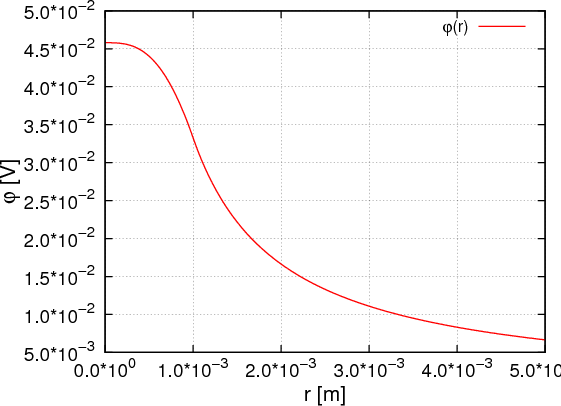
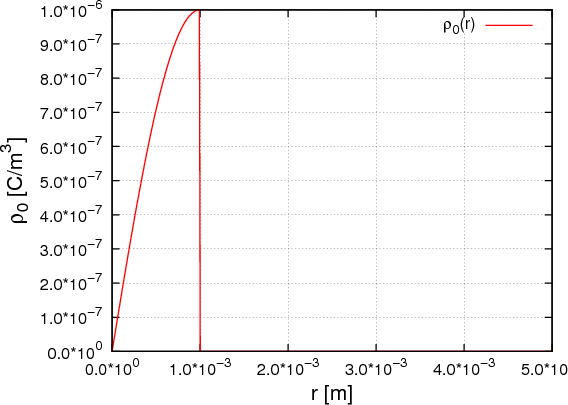
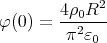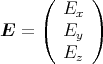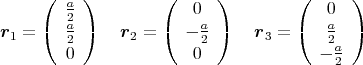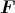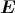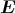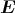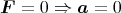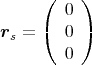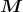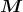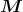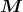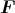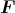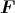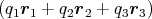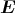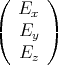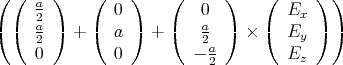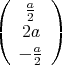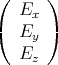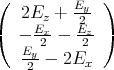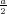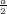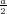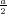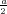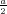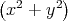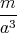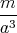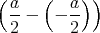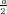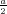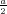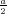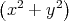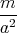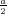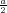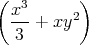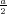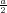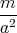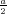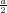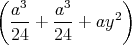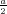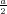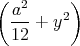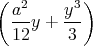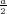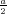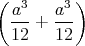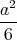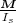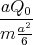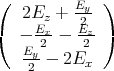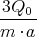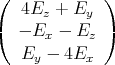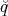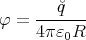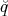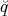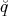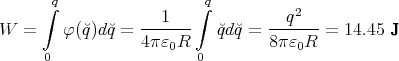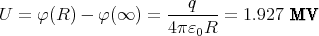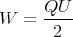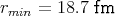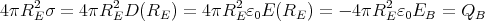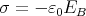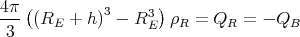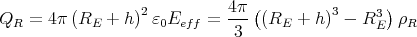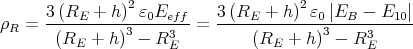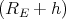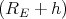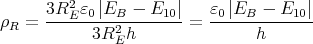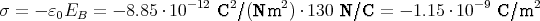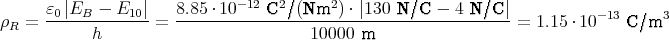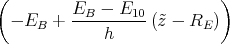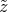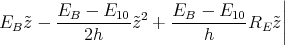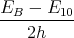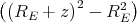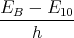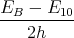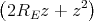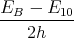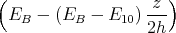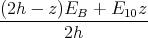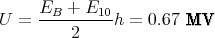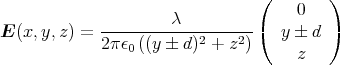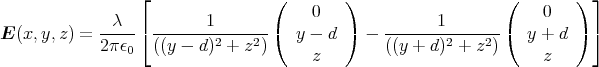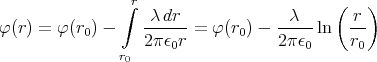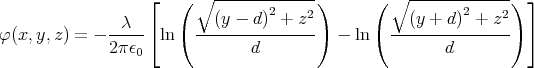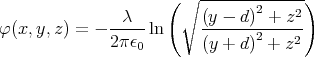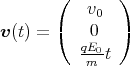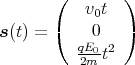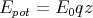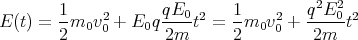ρ(r) = ρ0 sin(π ⋅r∕(2R). Berechnen Sie das elektrische Feld E(r) und das elektrostatische Potential U(r) für r = 0…∞.
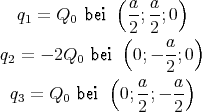 |
Der Würfel befindet sich in einem homogenen elektrischen Feld mit 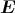 =
= 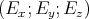 .
.
- Berechnen Sie die Kraft und das Drehmoment auf den Würfel, bezogen auf seinen Schwerpunkt.
- Wie gross sind die anfängliche Beschleunigung und die anfängliche Winkelbeschleunigung?
- Welche Arbeit W ist dazu erforderlich?
- Welche Spannung U liegt dann an der Kugel?
- Welche Beziehung folgt für W, U und q?
- Welche Flächenladungsdichte σ der Erdoberfläche und welche als homogen angenommene Raumladungsdichte ρ > 0 folgt aus den Angaben?
- Berechne den Potentialverlauf zwischen der Erdoberfläche und h = 10 km.
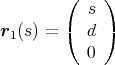
gegeben. Die Lage eines zweiten idealen Drahtes mit der Linienladungsdichte -λ ist durch die Gerade
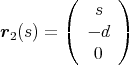
gegeben. Berechnen Sie für einen beliebigen Punkt P = (x,y,z) mit y≠±d das elektrische Feld und das Potential.
PDF-Version des Aufgabenblattes
Im Raum herrscht das elektrische Feld 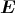 (x,y,z) = E0
(x,y,z) = E0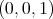 . Zur Zeit t = 0 hat
ein Teilchen der Masse m und der Ladung q die Geschwindigkeit
. Zur Zeit t = 0 hat
ein Teilchen der Masse m und der Ladung q die Geschwindigkeit 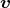 0 = v0
0 = v0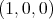 .
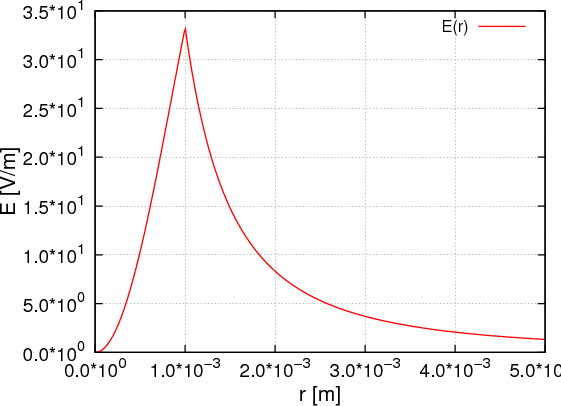
Berechne
.
Berechne
- die Geschwindigkeit
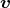 (t)
(t)
- den Ort
 (t)
(t)
- die Gesamtenergie Etot(t)
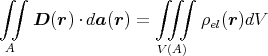
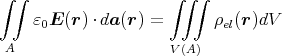
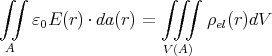
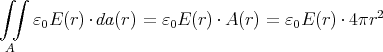
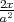
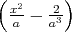
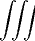
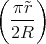
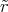
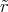
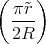
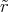
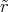
![[ (( ) ) ( 2 ) (( ) )]
--2˜r--sin -π- ˜r - (˜r-)-- ---2-- cos π-- r˜
( π-)2 2R π-- ( π-)3 2R
2R 2R 2R](uebungsblatt0325x.png)
![[ 2 ( ) ( 2 3) ( )]
8R--˜r π˜r- 2R-˜r- 16R-- π˜r-
π2 sin 2R - π - π3 cos 2R](uebungsblatt0326x.png)
![[ 2 ( ) ( 2 3 ) ( ) 3]
8R--r sin -πr - 2Rr-- - 16R-- cos πr- - 16R--
π2 2R π π3 2R π3](uebungsblatt0327x.png)
![[ 4Rr ( πr ) ( 8R2 ) ( πr ) 8R2 ]
----sin --- - r2 - --2- cos --- - --2-
π 2R π 2R π](uebungsblatt0328x.png)
![[ ( ) ]
2 4Rr ( πr ) 2 8R2 ( πr) 8R2
ε0E (r)⋅4πr = 8R ρ0 -π-- sin 2R- - r - -π2- cos 2R- - -π2-](uebungsblatt0329x.png)
![[ ( ) ]
2R-ρ0 4R- (πr-) 8R2-- ( πr-) 8R2--
E (r) = πε πr sin 2R - 1 - π2r2 cos 2R - π2r2
0](uebungsblatt0330x.png)
![[ ( ) ]
2R-ρ0 4R- (-πr) -8R2- ( πr-) -8R2- r-
E (r) = πε πr sin 2R - 1 - π2r2 cos 2R - π2r2 r
0](uebungsblatt0331x.png)
![[ ( ) ( ) ( ) ] [ ]
2R-ρ0 4R-- πR-- 8R2-- πR-- -8R2- 8ρ0R- -2
E (R ) = πε πR sin 2R - 1 - π2R2 cos 2R - π2R2 = π2ε 1 - π
0 0](uebungsblatt0332x.png)
![[ ]
R2-r- 8ρ0R3-- 2-
E (r ) = E(R )r2 r = π2ε r3 1 - π r
0](uebungsblatt0333x.png)
![{ [ ( ) ]
2Rρ0 4R-sin (-πr) - 1 - 8R222 cos (πr) - -8R222 r für r ≤ R
E (r) = πε0 πr 2R 3 [ π r ] 2R π r r
8πρ20εR0r3 1 - 2π r für r > R](uebungsblatt0334x.png)
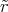
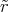
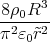
![[ ]
2
1 - --
π](uebungsblatt0339x.png)
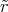
![[ ]
2-
1 - π](uebungsblatt0342x.png)
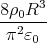
![[ ]
2-
1 - π](uebungsblatt0345x.png)
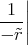
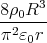
![[ ]
1 - 2-
π](uebungsblatt0348x.png)
![[ ]
8ρ0R2 2
φ (R) = --2--- 1 - --
π ε0 π](uebungsblatt0349x.png)
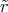
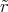
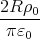
![[ ( ) ( 2) ( ) 2 ]
4R- π-˜r -8R-- π-˜r 8R---
π˜r sin 2R - 1 - π2 ˜r2 cos 2R - π2˜r2](uebungsblatt0353x.png)
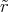
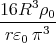
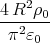
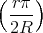
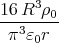
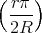
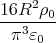
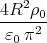
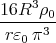
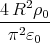
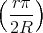
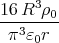
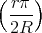
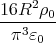
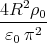
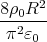
![[ ]
2-
1 - π](uebungsblatt0370x.png)
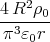
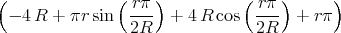
![{ 4R2ρ0 ( (r-π) (rπ) )
φ(r) = π3ε0r - 4 R + πr sin3 2R[ + 4]R cos 2R + rπ für r ≤ R
8πρ02Rε0r- 1 - 2π für r > R](uebungsblatt0373x.png)