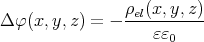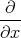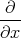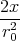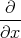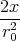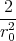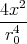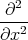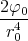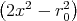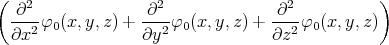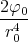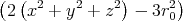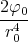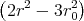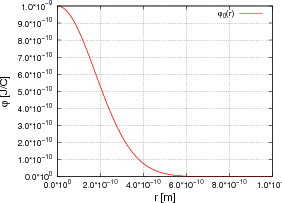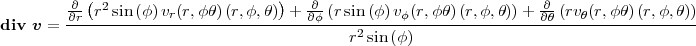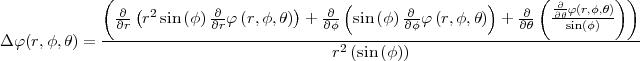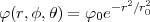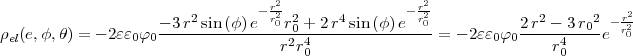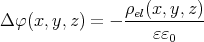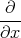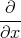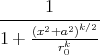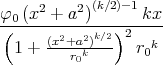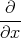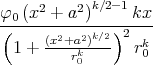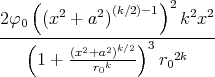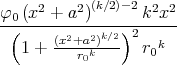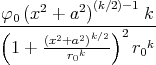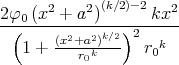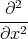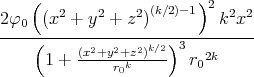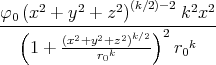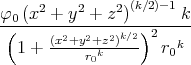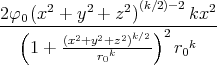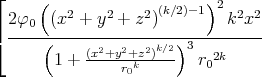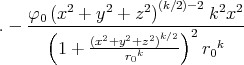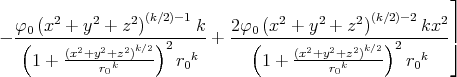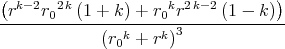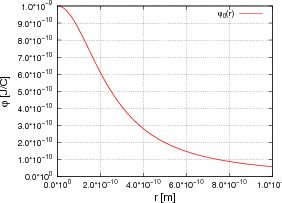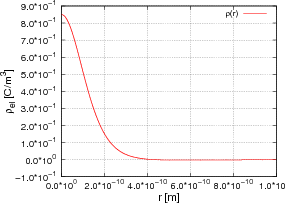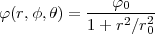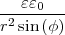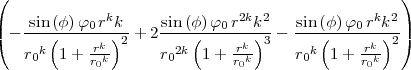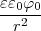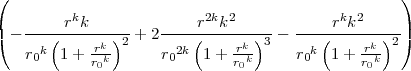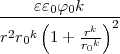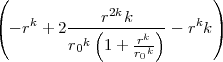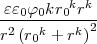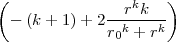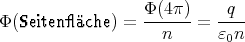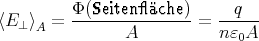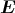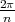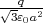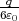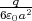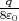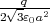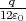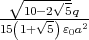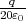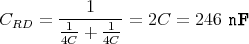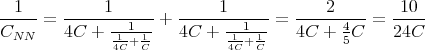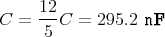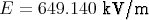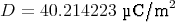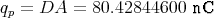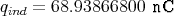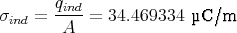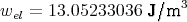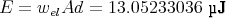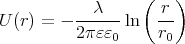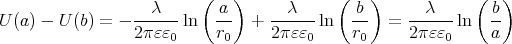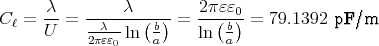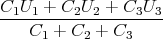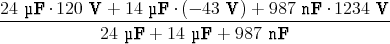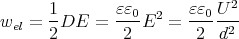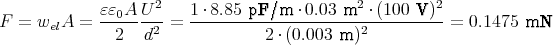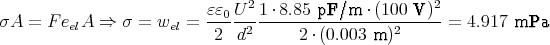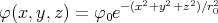
- Berechnen Sie die Ladungsverteilung ρel(x,y,z).
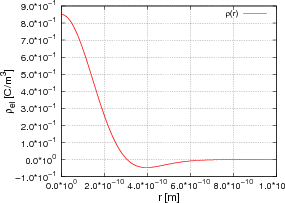
- Skizzieren Sie entlang der positiven x-Achse die Ladungsverteilung ρel(x,y,z).
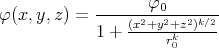
- Berechnen Sie die Ladungsverteilung ρel(x,y,z).
- Skizzieren Sie entlang der positiven x-Achse die Ladungsverteilung ρel(x,y,z).
- Tetraeder
- Hexaeder (Würfel)
- Oktaeder
- Dodekaeder
jeweils
- den Fluss des elektrischen Feldes durch eine Seitenfläche und
- das mittlere elektrische Feld (gemittelt über die Seitenfläche).
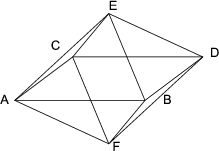
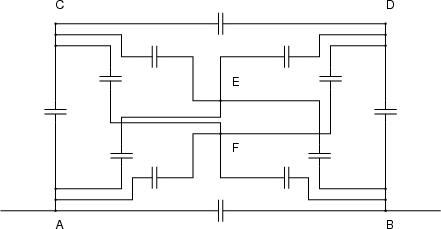
- Berechnen Sie die Kapazität entlang einer Raumdiagonale.
- Berechnen Sie die Kapazität zwischen zwei benachbarten Ecken.
- Berechnen Sie die Kapazität zwischen zwei übernächsten Ecken.
- Wie gross ist das elektrische Feld E im Kondensator?
- Wie gross ist die dielektrische Verschiebung D im Kondensator?
- Wie gross ist die Ladung qP auf den Kondensatorplatten?
- Wie gross ist induzierte Ladungsdichte an der Grenze des Dielektrikums?
- Wie gross ist die Energiedichte we im Kondensator?
- Wieviel Energie ist im Kondensator gespeichert?
- Berechnen Sie allgemein (ohne Einsetzen) die Kapazität pro Länge (Kapazitätsbelag) eines solchen Kabels. (Berechnen Sie dazu am Besten die Potentialdifferenz zwischen Aussenleiter und Innenleiter bei gegebener Ladung pro Länge)
- Wie gross ist der Kapazitätsbelag, wenn a∕b = 3∕20 ist?
PDF-Version des Aufgabenblattes
- Berechnen Sie die Kraft F zwischen zwei Kondensatorplatten der Fläche A = 300 cm2 im Abstand d = 3 mm, wenn eine Spannung von U = 100 V zwischen den Platten herrscht.
- Wie gross muss die mechanische Zugspannung σ sein, damit die Platten in Ruhe sind?