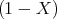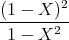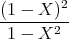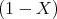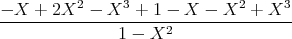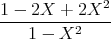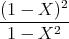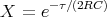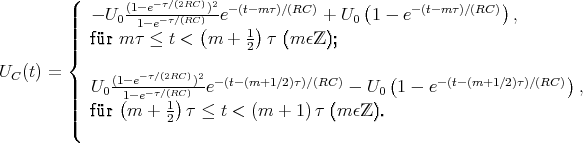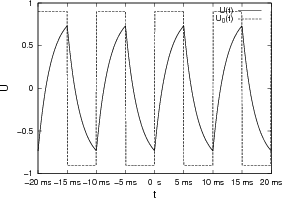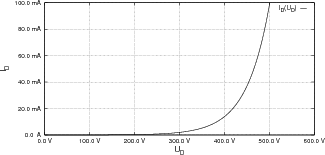
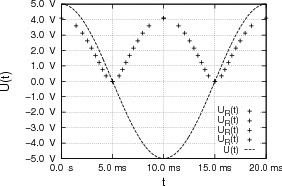
- Konstruieren Sie den zeitlichen Spannungsverlauf an R, wenn R = 100 Ω und U0 = 5 V ist.
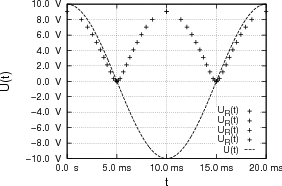
- Wie sieht der zeitliche Spannungsverlauf an R für U0 = 10 V aus?
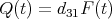
wobei d31 = 10-8 C/N = 10-8 m/V der sogenannte Piezomodul ist. Die entstehende Ladung wird auf den Platten, die auf der Keramik beidseitig aufgebracht wurden, gespeichert. Die Kapazität sei CP = 10 nF. Sie sei mit einem Widerstand R = 1 kΩ verbunden.

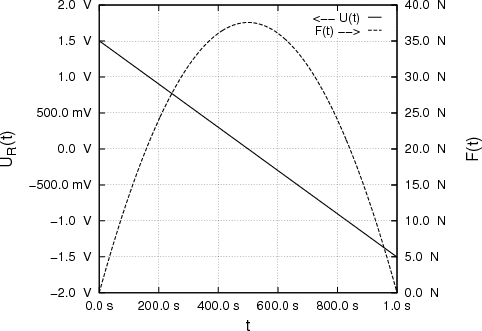
Eine Stahlkugel mit einem Durchmesser von 10 mm und einer Masse m = 4.0 g falle aus der Höhe h0 = 50 cm auf den Piezo und deformiere ihn mit der aus der Impulsänderung resultierenden Kraft. Die Zeitabhängige Kraft sei parabelförmig. Der Kontakt dauert insgesamt τ = 1 ms. Berechnen Sie U(t) am Widerstand während des Stosses.
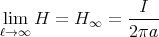
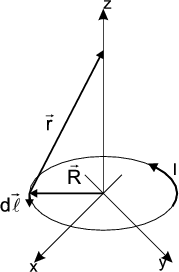
- Man berechne mit dem Gesetz von Biot-Savart das Magnetfeld
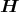 eines Kreisstromes
entlang seiner Symmetrieachse z!
eines Kreisstromes
entlang seiner Symmetrieachse z!
- Welcher Strom muss in einem Ring mit dem Durchmesser 2R = 2 cm fliessen, wenn das Feld im Zentrum des Kreisstromes gerade das Erdmagnetfeld (Magnetische Induktion BE ≈ 50 µT kompensieren soll?
- In welcher Entfernung vom Zentrum in Richtung z beträgt die vom Kreisstrom erzeugte magnetische Induktion noch 0.1BE?
PDF-Version des Aufgabenblattes
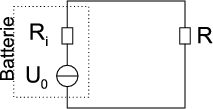
Zeigen Sie mit der Bedingung, dass ein Leiterbahnknoten sich nicht auflädt, die Gültigkeit des ersten Kirchhoffschen Gesetzes. (Die Summe der zufliessenden Ströme an einem Knoten ist gleich der Summe der wegfliessenden Ströme.)
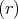
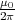
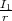
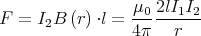
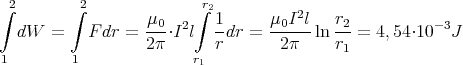
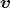
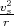
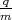
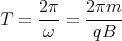
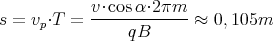


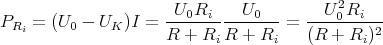
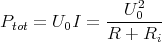
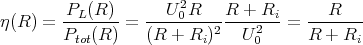
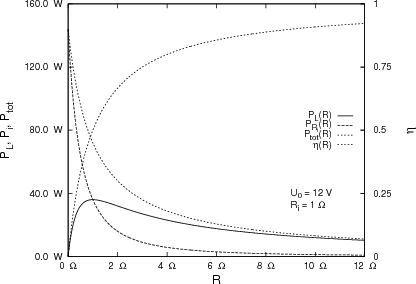
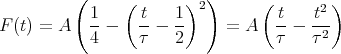
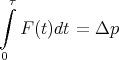
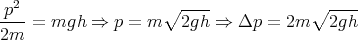
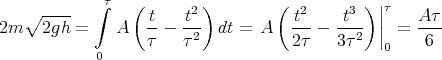
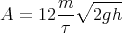
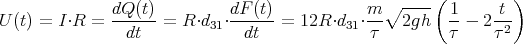
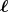

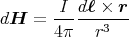
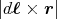
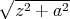
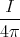
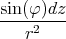
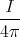
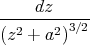
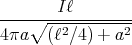
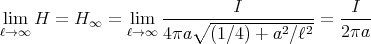

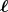

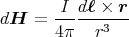
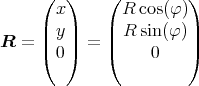
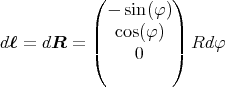
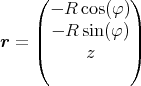
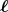

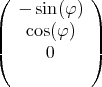
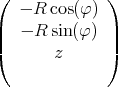
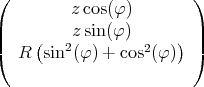
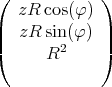
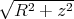
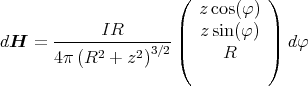
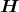
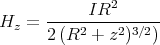
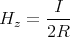
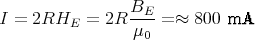
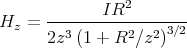
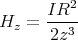
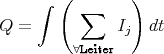
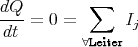
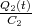
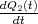
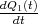
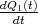
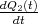
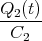
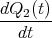
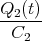
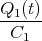
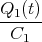
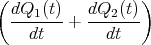
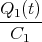
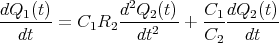
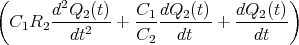
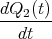
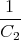
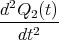
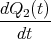
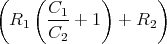
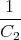
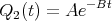
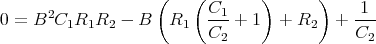
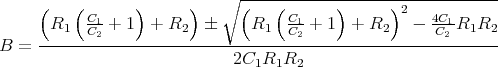
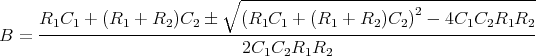
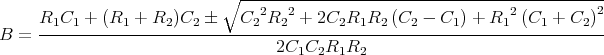
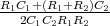
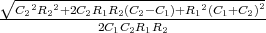
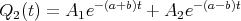
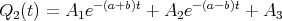
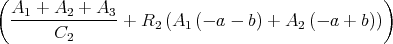
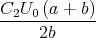
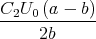
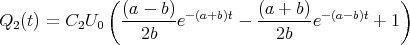
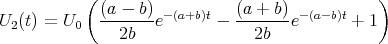
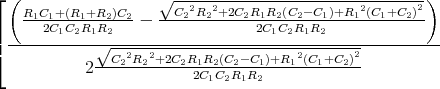
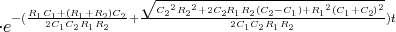
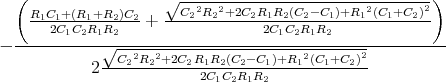
![√ --2--2---------------2------2 ]
-(R1C21C+(RC1+RRR2)C2---C2-R2+2C2R21CR2C(C2R-CR1)+R1-(C1+C2)-)t
⋅e 1 2 1 2 1 2 1 2 + 1](uebungsblatt07111x.png)
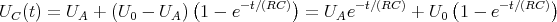
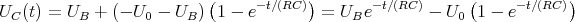
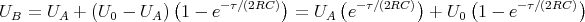
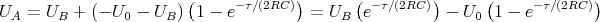
![[U (e-τ∕(2RC )) + U (1 - e-τ∕(2RC ))]
A 0](uebungsblatt07116x.png)
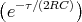
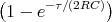
![[UAX + U0 (1 - X )]](uebungsblatt07119x.png)