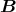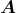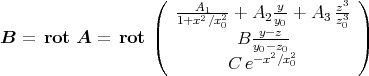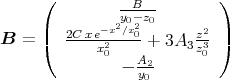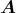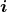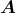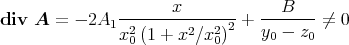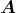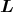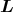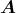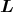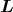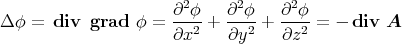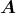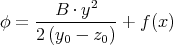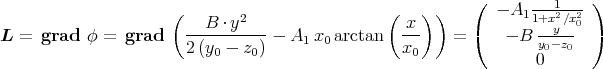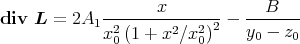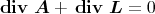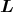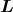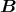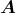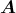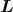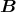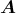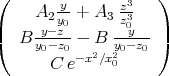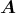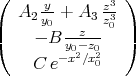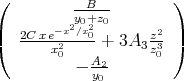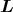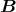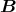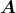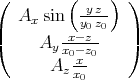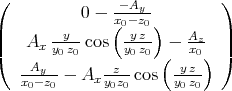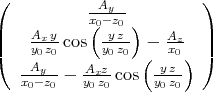- Die Kraft auf einen stromdurchflossenen Leiter im Magnetfeld ist
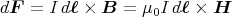
Hier sind die Leiterstücke d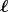 und das Magnetfeld
und das Magnetfeld 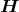 senkrecht aufeinander, also:
senkrecht aufeinander, also:
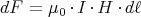
Mit der Stromdichte i und dem Drahtquerschnitt A ergibt sich
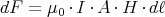
oder, für den L langen Draht mit Volumen V = A⋅L
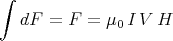
Diese Kraft wirkt horizontal. Die Komponente senkrecht zum Pendel ist
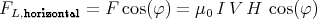
Bei einer Auslenkung eines Pendels der Masse M um den Winkel φ ist die rücktreibende
Kraft
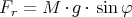
Die Kraft im Magnetfeld ist gleich dieser mechanischen Kraft, also (mit M = ρM V )
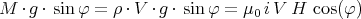
⇒
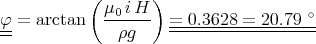
- Die Fluggeschwindigkeit der Ionen mit Ladung e berechnet sich aus der Energie W = eU,
die die Ionen im elektrischen Feld, das mit der Spannungsdifferenz U erzeugt wurde,
erhalten, die gleichzeitig die kinetische Energie W =
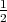 mv2 ist, zu
mv2 ist, zu
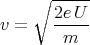
Die Masse m eines Ions ist die Molmasse M dividiert durch die Avogadro-Zahl
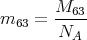
(Die Dichteangabe wird nicht benötigt).
- In einem Magnetfeld wirkt auf ein geladenes Teilchen, das sich bewegt, die Lorentzkraft
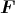 = q
= q 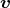 ×
×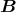 . Da
. Da 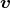 senkrecht zu
senkrecht zu 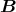 ist, kann hier mit den Beträgen gerechnet werden und
die Flugbahn ist ab Eintritt ins Magnetfeld eine Kreisbahn, deren Radius r
sich aus der Gleichheit der mechanischen Zentrifugalkraft und Lorentzkraft
ergibt.
ist, kann hier mit den Beträgen gerechnet werden und
die Flugbahn ist ab Eintritt ins Magnetfeld eine Kreisbahn, deren Radius r
sich aus der Gleichheit der mechanischen Zentrifugalkraft und Lorentzkraft
ergibt.
| ev ⋅B | = m63 ⋅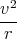 | |
|
| ⇒ r63 | = 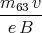 = = 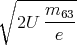 ⋅ ⋅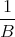 | |
|
| = 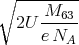 ⋅ ⋅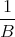 = = 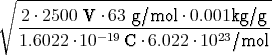 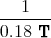 = 0.317 m = 0.317 m | | |
- für die etwas schwereren 65Cu-Ionen ergibt sich
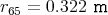
- Die Ionen werden senkrecht zur Flugrichtung und senkrecht zum Feld abgelenkt.
Die Auffangplatte muss deshalb parallel zum Feld orientiert sein, damit die
Ionen senkrecht auftreffen. Der Abstand (D = 32 cm) ist für diesen Fall richtig
gewählt.
- Der Abstand ΔL der Auftreffstellen ist die Differenz der Kreisbahnradien, also
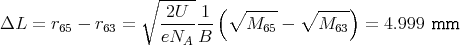
- Die Kraft auf ein bewegtes geladenes Teilchen im kombinierten elektrischen und magnetischen
Feld ist:
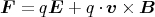
- Wenn das Teilchen sich gleichförmig bewegen soll, muss diese Kraft null sein, also
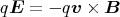
oder
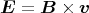
unabhängig von der Masse des Teilchens und der Ladung, aber abhängig von dessen
Geschwindigkeit. Die Felder müssen also senkrecht zueinander sein und das Teilchen
muss sich senkrecht zu beiden bewegen. Bei einem bestimmten 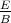 Wert werden sich
nur die Teilchen mit v =
Wert werden sich
nur die Teilchen mit v = 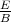 geradlinig bewegen.
geradlinig bewegen.
- So eine Anordnung ist also ein Geschwindigkeitsfilter für geladene Teilchen.
-
Das Ampèresche Durchflutungsgesetz
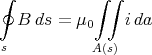
verbindet das Magnetfeld B mit den Stromdichten i.
Bei einer zylindersymmetrischen Anordnung der Stromdichten muss das Ergebnis ebenfalls
Zylindersymmetrie aufweisen, das Magnetfeld muss also kreisförmig sein und dessen Stärke darf
nur vom Radius abhängen und nicht vom Ort entlang des Leiters. Damit vereinfacht sich das
Wegintegral, wenn als Weg ein konzentrischer Kreis (zur Leiteranordnung) mit Radius r gewählt
wird, zu
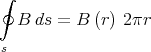
Das Flächenintegral (mit obigen Kreis als Umrandung) ergibt für
- Innenleiter: r < R1 mit i =
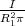
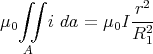
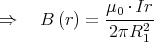
- Zwischenraum: R1 < v < R2 Strom nur im Innenleiter,
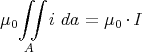
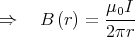
- Aussenleiter: R2 < r < R3 Strom im Innenleiter und im Teil des Aussenleiters (mit
anderer Richtung)
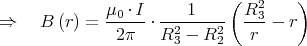
- Aussenraum: r > R3 Gesamtstrom im Inneren des Kreises ist I - I = 0
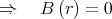
Das Feld steigt also linear an bis zum Radius R1, fällt dann hyperbelförmig ab bis zum Radius
R2 und von da an stärker bis zu R3, wo es Null wird. Ausserhalb des Koaxialkabels existiert kein
Magnetfeld, das von den Strömen im Kabel herrührt. Ebenso ist, wenn Innenleiter und
Aussenleiter mit der gleichen Ladungsdichte belegt sind, das elektrische Feld aussen gleich
null.
- Wir setzen r =
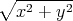 und lassen den Strom I entlang der z-Achse fliessen. Wir wollen
zeigen, dass
und lassen den Strom I entlang der z-Achse fliessen. Wir wollen
zeigen, dass
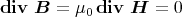
ist. Das Magnetfeld ist tangential, der Einheitsvektor, der in Richtung des Magnetfeldes zeigt,
sei
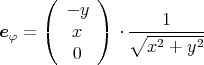
div 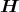 | = div 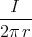  φ φ | | | |
|
| = div 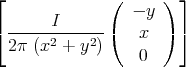 | | | |
|
| =  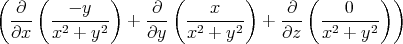 | | | |
|
| = 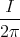 ![[ ( ) ( ) ]
- --- y-⋅2x- + - ---x⋅2y---
(x2 + y2)2 (x2 + y2)2](uebungsblatt0871x.png) | | | |
|
| = 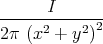 ![[2y x - 2x y]](uebungsblatt0873x.png) | = | 0 | | | |
|
| | | | |
-
- Die magnetische Induktion
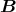 berechnet sich aus dem Vektorpotential
berechnet sich aus dem Vektorpotential 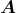 über
über
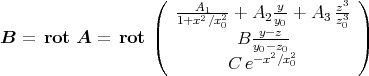
Hier ergibt sich
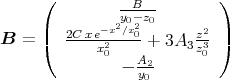
- Damit Δ
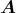 = μ0
= μ0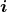 erfüllt ist, muss div
erfüllt ist, muss div 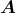 = 0 sein.
= 0 sein.
Hier ergibt sich
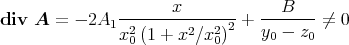
- Um das Problem zu lösen, muss zum Vektorpotential
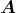 ein Potential
ein Potential 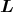 addiert
werden, für das div
addiert
werden, für das div 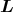 = -div
= -div 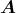 und rot
und rot 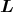 = 0 gilt. Wir suchen also ein
Potential ϕ, so dass grad ϕ =
= 0 gilt. Wir suchen also ein
Potential ϕ, so dass grad ϕ = 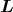 ist. Also ist auch
ist. Also ist auch
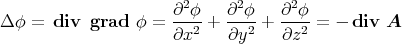
In div 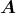 taucht der konstante Term B∕(y0 -z0) sowie ein von x abhängiger Term
auf. Den konstanten Term kann man mit der zweiten Ableitung nach y oder der
zweiten Ableitung nach z bekommen. Wir verwenden y und haben
taucht der konstante Term B∕(y0 -z0) sowie ein von x abhängiger Term
auf. Den konstanten Term kann man mit der zweiten Ableitung nach y oder der
zweiten Ableitung nach z bekommen. Wir verwenden y und haben
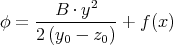
Der x-Term hat die Form x∕(x2 + x
02)2). Das doppelte Integral dazu ist in den
Hinweisen angegeben, so dass wir für ϕ bekommen:

Damit bekommen wir
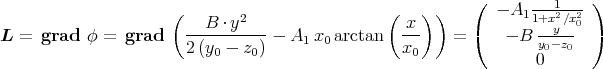
sowie
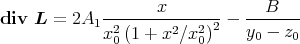
und
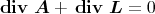
- Da wir
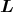 = grad ϕ gesetzt hatten, ist rot
= grad ϕ gesetzt hatten, ist rot 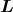 = rot grad ϕ ≡ 0. Also ist die
magnetische Induktion
= rot grad ϕ ≡ 0. Also ist die
magnetische Induktion 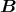 des neuen Vektorpotential
des neuen Vektorpotential 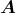 ′ =
′ = 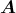 +
+ 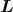
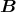 | = rot 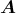 ′ = rot ′ = rot 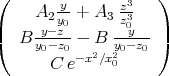 = rot = rot 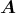 ′ = rot ′ = rot 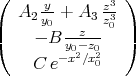 | |
|
| = 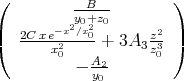 | | |
wie bei Teilaufgabe a).
Bei genauerer Überlegung zeigt sich, dass wir mit 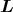 letztlich einfach aus der x-Komponente von
A die x-Abhängigkeit, aus der y-Komponente die y-Abhängigkeit und aus der z-Komponente die
z-Abhängigkeit entfernt hatten.
letztlich einfach aus der x-Komponente von
A die x-Abhängigkeit, aus der y-Komponente die y-Abhängigkeit und aus der z-Komponente die
z-Abhängigkeit entfernt hatten.
- Die magnetische Induktion
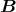 berechnet sich aus dem Vektorpotential zu
berechnet sich aus dem Vektorpotential zu
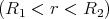 ,
,
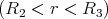
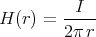
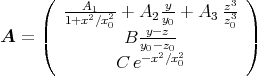
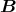 .
.
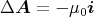
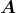 ergänzt werden, damit dies zutrifft?
ergänzt werden, damit dies zutrifft?
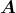 ebenfalls die magnetische Induktion
ebenfalls die magnetische Induktion 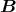 .
.
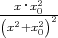 = -
= -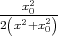
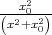 = x0 arctan
= x0 arctan 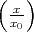
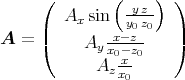
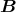 .
.
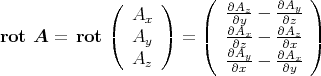
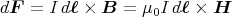
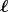
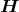
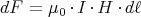
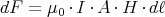
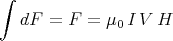
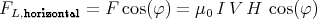
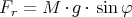
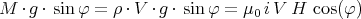
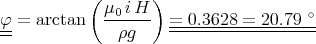
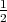
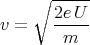
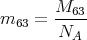
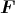
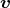
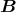
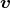
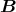
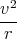
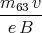
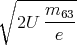
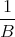
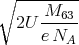
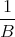
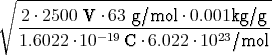
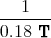
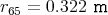
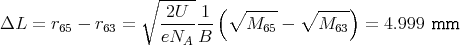
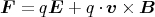
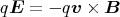
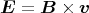
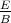
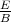
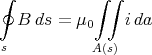
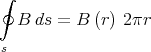
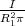
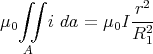
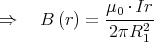
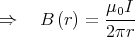
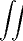
![[ ]
----I---- ( 2 2)
I - R2 - R2 ⋅ r - R 2
3 2](uebungsblatt0857x.png)
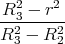
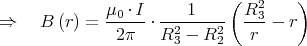
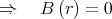
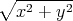
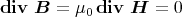
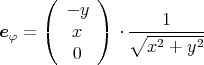
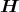
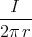

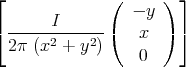
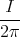
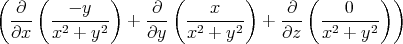
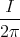
![[ ( ) ( ) ]
- --- y-⋅2x- + - ---x⋅2y---
(x2 + y2)2 (x2 + y2)2](uebungsblatt0871x.png)
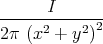
![[2y x - 2x y]](uebungsblatt0873x.png)