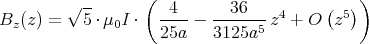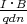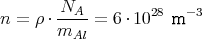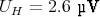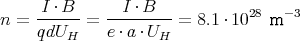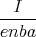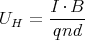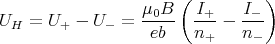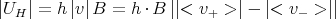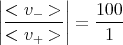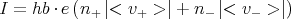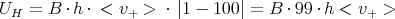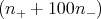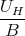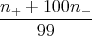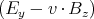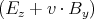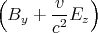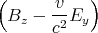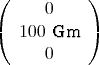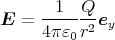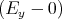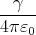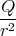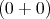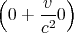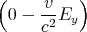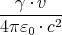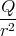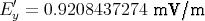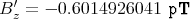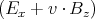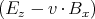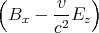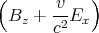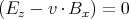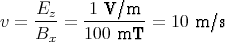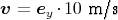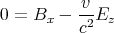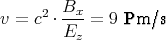- Das magnetische Moment m ist für eine Leiterschleife definiert als
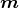 = A
= A A ⋅I, wobei
A ⋅I, wobei
 A der Normalenvektor auf die Fläche A der Schleife ist. Für eine kurze Spule mit N
Windungen ergibt sich einfach:
A der Normalenvektor auf die Fläche A der Schleife ist. Für eine kurze Spule mit N
Windungen ergibt sich einfach:
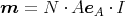
Für die angegebene Spule ergibt sich daraus
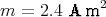
Das magnetische Moment zeigt in Richtung der Spulenachse.
Das Drehmoment in einem Magnetfeld auf einen Körper mit magnetischen Moment
berechnet sich zu
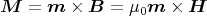
Mit der angegebenen Orientierung zwischen Feld und Spule ergibt sich
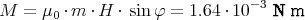
- Die magnetische Induktion entlang der Symmetrieachse einer (sehr kurzen) Spule mit N
Windungen sei angenähert die einer einzelnen Windung mit N -fachen Strom.
Die magnetische Induktion einer kreisförmigen Schleife mit Radius R, durch die der Strom
I fliesst, im Abstand ζ zum Kreismittelpunkt auf der „Achse“ des Kreises berechnet sich
mit Biot-Savart zu
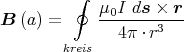
Bei Benutzung von φ und R zur Beschreibung des Kreises ergibt sich für die Position ζ
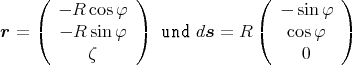
wodurch
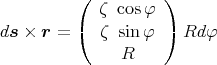
wird.
Die Integration über φ mit den Grenzen 0 und 2π liefert damit:
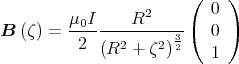
also nur eine Komponente in Richtung der z-Achse.
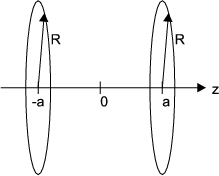
Um die Homogenität in der Mitte beider Spulen zu prüfen, wählen wir eine Position
-a ≤ z ≤ a aus. Die Abstände sind dann ζ1 = a - z und ζ2 = a + z.
Das Magnetfeld ist die Summe der beiden Anteile, also
Damit ergibt sich:
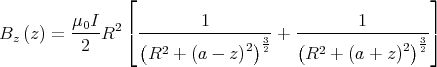
Damit das Magnetfeld homogen ist, muss der Klammerausdruck in einem möglichst grossem
Bereich z um 0 konstant sein, also von z nicht abhängen. Also muss die Ableitung von Bz nach
z an der Stelle 0 in möglichst hoher Ordnung null sein. Um die Berechnung zu erleichtern, wird
die Klammer zuerst umgeschrieben:
z soll klein sein, so dass um z = 0 eine Taylorentwicklung sinnvoll sein sollte, die hier nach dem
quadratischen Term in z abgebrochen wird, (wobei der Faktor vor der Klammer jetzt wieder
weggelassen wird):
| K2 | = 1 +  ⋅ ⋅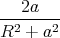 ⋅z + ⋅z +  ⋅ ⋅ ![[ ( )2 ]
5⋅ --2a---- - ---2----
2 R2 + a2 R2 + a2](uebungsblatt0935x.png) z2 z2 | |
|
| + 1 - 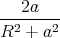 ⋅z + ⋅z +  ⋅ ⋅ ![[ ( )2 ]
5- ---2a--- ----2---
2 ⋅ R2 + a2 - R2 + a2](uebungsblatt0940x.png) z2 z2 | |
|
| = 2 +  ![[ ]
---10a2---- ---2----
(R2 + a2)2 - R2 + a2](uebungsblatt0942x.png) z2 z2 | | |
Dieser Ausdruck wird unabhängig von z, wenn R = 2a gilt, also der Durchmesser der Spulen
doppelt so gross ist wie ihr Abstand.
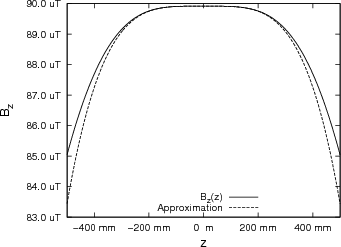
In diesem Falle ist die Reihenentwicklung für Bz
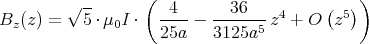
Das Feld ist also bis und mit der dritten Ableitung flach.
(Berechnung mit N = 100, I = 1 A, a = 0.5 m.)
- Die Hall-Spannung beträgt UH =
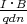 (q = Ladung der Ladungsträger, d = Strecke des
Magnetfeldes in der Probe, n = Ladungsträgerdichte). Die Ladungsträgerdichte ist hier die
Atomdichte die
(q = Ladung der Ladungsträger, d = Strecke des
Magnetfeldes in der Probe, n = Ladungsträgerdichte). Die Ladungsträgerdichte ist hier die
Atomdichte die
(mit ρ = Dichte = 2700 kg/m3, m
AL = 27 gmol, NA = 6 ⋅ 1023 mol-1) sich zu
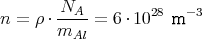
ergibt.
Mit d = a = 0.1 mm, q = eElektron = 1.6 ⋅ 10-19 A s erhält man
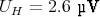
- Nach der gleichen Formel wie in Aufgabe 1 ergibt sich (Dicke d = a, Ladung q = e):
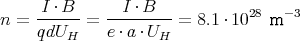
Die mittlere Geschwindigkeit berechnet sich aus dem Strom (mit Höhe h = b) zu
| I | = q ⋅n⋅h⋅d < v > ⇒ | |
|
| < v >= 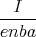 = 3.1 ⋅ 10-4 m/s = 3.1 ⋅ 10-4 m/s | | |
- Die Hallspannungen berechnen sich gemäss
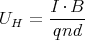
bei einer Stromstärke I in einem Material der Dicke d mit Ladungsträgern mit Ladung
q der Konzentration n in einem Magnetfeld B senkrecht zur Stromrichtung und
senkrecht zum Material. Die Spannung ist senkrecht zum Magnetfeld und senkrecht zur
Stromrichtung.
Sowohl positive geladene Ladungsträger wie die negativen werden in die gleiche Richtung in der
Sonde ausgelenkt, so dass nur die Differenz beider wirksam ist.
Die Hallspannung ist also bei Vorhandensein von positiven und negativen Ladungsträgern:
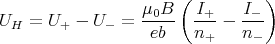
andererseits gilt:
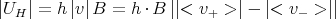
Wenn nun
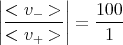
ist, so kann der Gesamtstrom
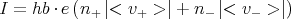
berechnet werden, der nötig ist, um die geforderte Hallspannung UH = 10-9V beim
vorhandenen Magnetfeld B = 5μT zu erreichen:
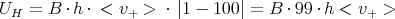
| I | = b⋅e⋅h < v+ > ⋅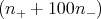 | |
|
| = be⋅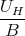 ⋅ ⋅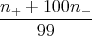 = 325A = 325A | | |
Dieser grosse Strom ist nötig, da die Ladungsträgerkonzentration gross ist.
Sinnvoller wäre es, ein Material zu verwenden, dessen Ladungsträgerkonzentration sehr viel
kleiner ist, z.B. einen dotierten Halbleiter.
- Sie fliegen in die x-Richtung. Die Lorentztransformation für die Felder lautet dann
| Ex′ | = Ex | |
|
| Ey′ | = γ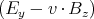 | |
|
| Ez′ | = γ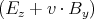 | |
|
| Bx′ | = Bx | |
|
| By′ | = γ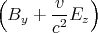 | |
|
| Bz′ | = γ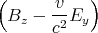 | |
|
| | |
Das elektrische Feld bei  =
= 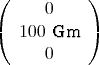 ist
ist
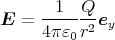
Es hat also eine y-Komponente. Alle anderen Felder sind null. Im Ruhesystem des Raumschiffes
ist dann mit
| Ex′ | = 0 | | | |
|
| Ey′ | = γ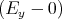 | = | 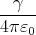 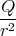 | | | |
|
| Ez′ | = γ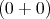 | | | |
|
| Bx′ | = 0 | | | |
|
| By′ | = γ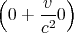 | | | |
|
| Bz′ | = γ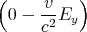 | = | -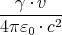 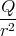 | | | |
|
| | | | |
Mit den Zahlenwerten bekommen wir Ey = 0.9022389061 mV/m und
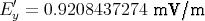
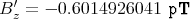
- Die Felder sind

Wenn wir die Lorentztransformationen anschauen,
| Ex′ | = γ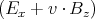 | |
|
| Ey′ | = Ey | |
|
| Ez′ | = γ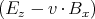 | |
|
| Bx′ | = γ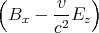 | |
|
| By′ | = By | |
|
| Bz′ | = γ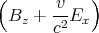 | | |
sehen wir, dass eine Geschwindigkeit in die y-Richtung Ez′ zum Verschwinden bringen
könnte.
Aus
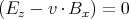
bekommen wir
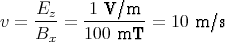
und
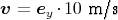
-
Die Felder sind gleich wie vorher, aber Bx soll im bewegten Bezugssystem null sein. Also
muss
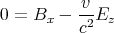
sein. Die Geschwindigkeit ist dann in die y-Richtung und hat den Betrag
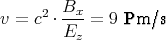
Diese Aufgabe ist, ausser in Science Fiction-Romanen, nicht lösbar!
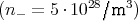 hergestellt werden. Für die
Beweglichkeiten gelte
hergestellt werden. Für die
Beweglichkeiten gelte  = 100. Die Ladungen beider Träger seien jeweils
Elementarladungen. Mit dieser Sonde soll das Erdmagnetfeld
= 100. Die Ladungen beider Träger seien jeweils
Elementarladungen. Mit dieser Sonde soll das Erdmagnetfeld 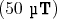 auf 10% genau
ausgemessen werden. Es steht dafür eine einstellbare Stromquelle und ein Voltmeter zur
Verfügung, das auf 1 nV genau misst. Welchen Strom muss die Stromquelle mindestens liefern?
Diskutiere das Ergebnis und mache Vorschläge zu einer verbesserten Ausführung einer
Hallsonde.
auf 10% genau
ausgemessen werden. Es steht dafür eine einstellbare Stromquelle und ein Voltmeter zur
Verfügung, das auf 1 nV genau misst. Welchen Strom muss die Stromquelle mindestens liefern?
Diskutiere das Ergebnis und mache Vorschläge zu einer verbesserten Ausführung einer
Hallsonde.
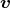 R = 0.2c⋅
R = 0.2c⋅ x an einer elektrostatisch
geladenen Sonne vorbei. Die Sonne trägt die Ladung QS = 1 GC. Sie hat den Durchmesser
DS = 1 Gm. Der Ursprung des kartesischen Koordinatensystems sei am Mittelpunkt der Sonne.
Sie befinden sich zur Zeit t = 0 bei
x an einer elektrostatisch
geladenen Sonne vorbei. Die Sonne trägt die Ladung QS = 1 GC. Sie hat den Durchmesser
DS = 1 Gm. Der Ursprung des kartesischen Koordinatensystems sei am Mittelpunkt der Sonne.
Sie befinden sich zur Zeit t = 0 bei
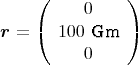


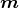


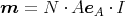
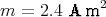
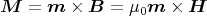
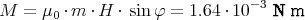
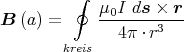
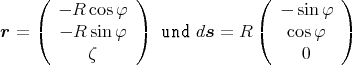
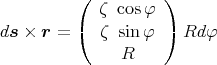
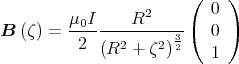
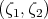
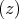
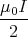
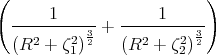
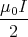
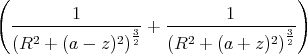
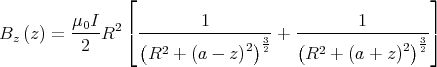
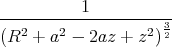
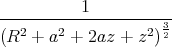
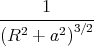
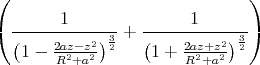

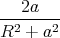


![[ ( )2 ]
5⋅ --2a---- - ---2----
2 R2 + a2 R2 + a2](uebungsblatt0935x.png)

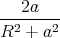


![[ ( )2 ]
5- ---2a--- ----2---
2 ⋅ R2 + a2 - R2 + a2](uebungsblatt0940x.png)

![[ ]
---10a2---- ---2----
(R2 + a2)2 - R2 + a2](uebungsblatt0942x.png)