©2005-2017 Ulm University, Othmar Marti, 
[Nächste
Seite] [Vorherige Seite] [vorheriges Seitenende] [Seitenende]
[Ebene nach oben] [PDF-Datei][Epub-Datei][Andere
Skripte]
2.10 Zusammenfassung: die Grundgleichungen der
Elektrostatik
-
Permittivität
- Gleichung (2.4)
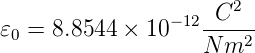
-
Coulomb-Gesetz
- Gleichung (2.5)
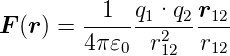
-
Elektrisches Feld
- Gleichung (2.2)
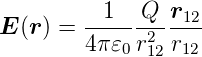
-
Elektrische Feldlinien
-
- Elektrische
Feldlinien beginnen bei der positiven Ladung
und enden bei der negativen Ladung.
- Die Anzahl der von einer Ladung ausgehenden
oder auf einer Ladung endenden Feldlinien ist
proportional zur Ladungsmenge.
- Ihre Dichte ist proportional zum elektrischen
Feld.
-
Elektrisches Feld einer kontinuierlichen Ladungsverteilung
-
Gleichung (2.5)
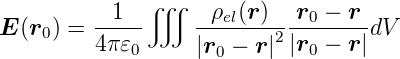
-
Ladung in einem Raumgebiet
- Gleichung (2.1)
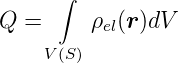
-
dielektrische Verschiebung
- Gleichung (2.4)
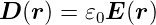
-
elektrischer Fluss
- Φ = ∫
Oberfläche
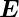 ·d
·d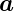
-
Gausssches Gesetz
- Gleichung (2.3)
-
Differentialform des Gaussschen Gesetzes
- Gleichung
(2.8)
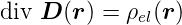
-
Leiter
- Leiter haben in ihrem Inneren keine statischen
elektrischen Felder.
-
Potentielle Energie einer Probeladung
- Gleichung (2.4)
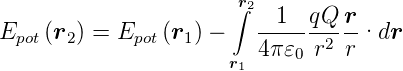
-
Elektrostatisches Potential und Spannung
- Gleichung
(2.11)
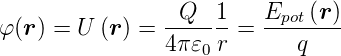
-
Potentielle Energie und Potential
- Gleichung (2.14)
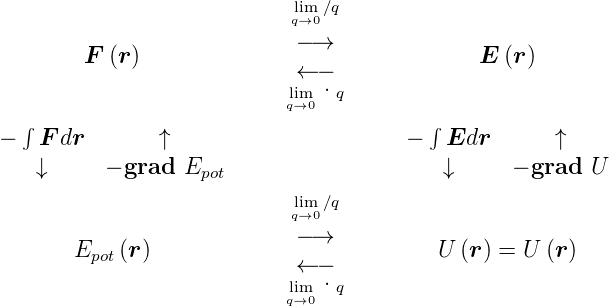
-
Potential einer kontinuierlichen Ladungsverteilung
-
Gleichung (2.17)
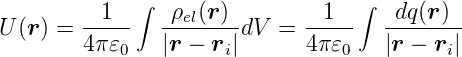
-
Poisson-Gleichung
- Gleichung (2.4)
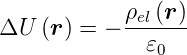
-
Kapazität
- Gleichung (2.4)
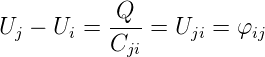
-
Parallelschaltung von Kondensatoren
- Gleichung (2.14)
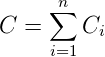
-
Reihenschaltung von Kondensatoren
- Gleichung (2.17)
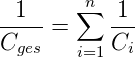
-
Energiedichte des elektrostatischen Feldes
- Gleichung
(2.7)
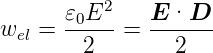
-
Maxwell-Spannung
- Gleichung (2.10) und Gleichung
(2.12)
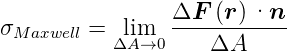
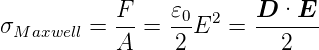
-
induziertes Dipolmoment
- Gleichung (2.8)
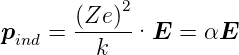
-
Lorentz-Beziehung
- Gleichung (2.24)
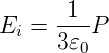
-
dielektrische Suszeptibilität
- Gleichung (2.15)
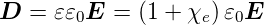
-
Stetigkeit der Feldkomponenten
- An der Grenzfläche
zweier Dielektrika gilt
- die Komponente der dielektrischen
Verschiebung senkrecht zur Grenzfläche und
- die Komponente des elektrischen Feldes parallel
zur Grenzfläche
sind stetig.
-
Stetigkeitsbedingung für das Potential
-
[Nächste Seite] [Vorherige Seite] [vorheriges Seitenende]
[Seitenanfang] [Ebene nach oben]
©2005-2017 Ulm
University, Othmar Marti,  Lizenzinformationen
Lizenzinformationen
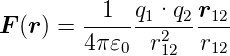
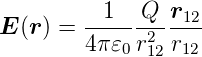
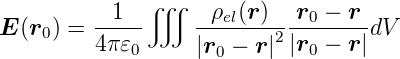
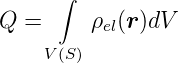
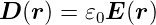
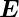 ·d
·d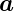
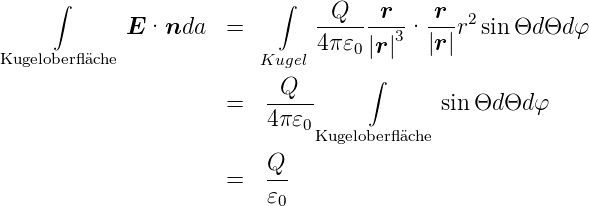
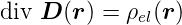
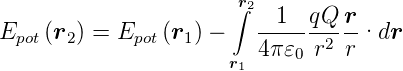
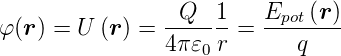
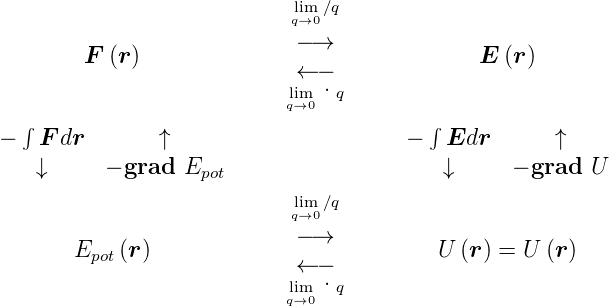
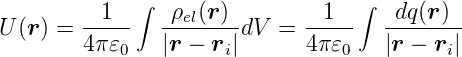
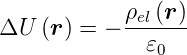
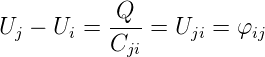
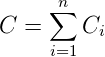
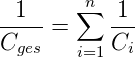
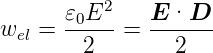
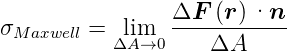
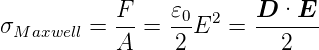
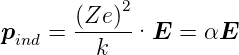
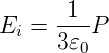
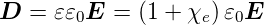
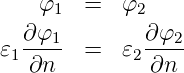

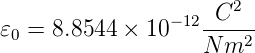
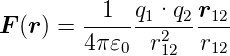
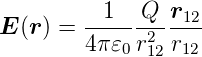
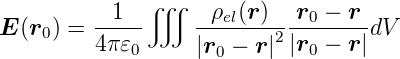
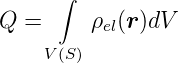
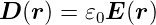
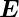 ·d
·d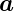
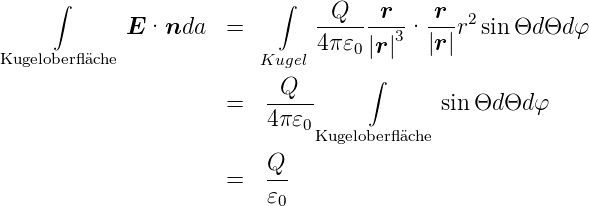
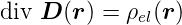
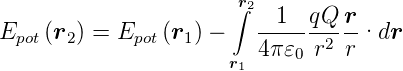
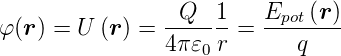
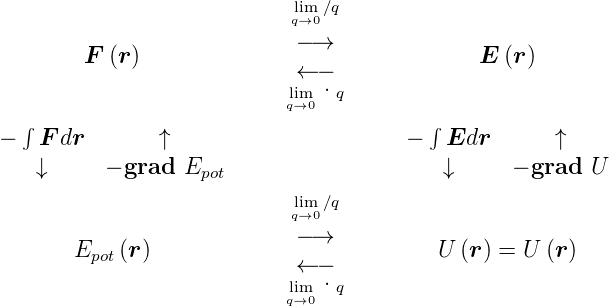
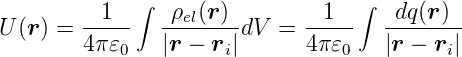
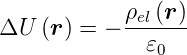
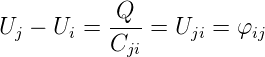
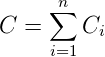
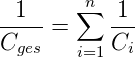
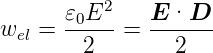
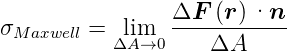
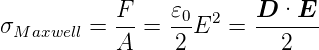
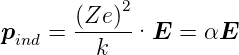
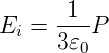
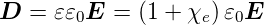
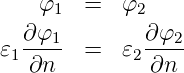
 Lizenzinformationen
Lizenzinformationen