__________________________________________________________________________
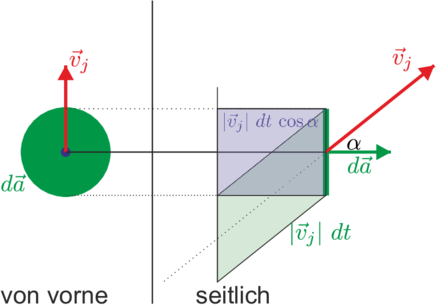
Berechnung des Stromes in einem Medium
_____________________________________________________________________

(Siehe Leisi, Klassische Physik II [Lei98, pp. 64])
__________________________________________________________________________

Berechnung des Stromes in einem Medium
_____________________________________________________________________
Wir betrachten Ladungsträger mit der einheitlichen
Ladung q. Die Ladungsträgerdichte nj habe die Geschwindigkeit
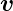 j.
j.
Der Strom δIj durch das Flächenelement d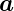 ist
ist
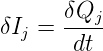 | (3.1) |
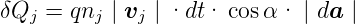 | (3.2) |
und damit
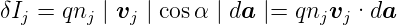 | (3.3) |
Der gesamte Strom der Ladungsträger q ist dann
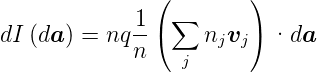 | (3.4) |
wobei n = Σnj ist.
Die mittlere Geschwindigkeit der Ladungsträger ist
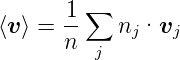 | (3.5) |
Wir definieren das Vektorfeld der Stromdichte
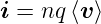 | (3.6) |
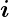 ist abhängig vom Ort, da auch n und
ist abhängig vom Ort, da auch n und 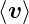 ortsabhängig
sind.
ortsabhängig
sind.
Der Strom bezüglich d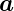 ist dann
ist dann
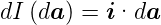 | (3.7) |
und, integriert,
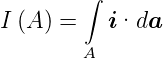 | (3.8) |
Diese Gleichung besagt, dass der Strom gleich dem Fluss des Stromdichtefeldes durch eine Fläche A ist.
Wird der Strom durch mehrere Arten von Ladungsträgern gebildet, schreibt man
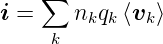 | (3.9) |
Beispiel:
Driftgeschwindigkeit in einem Kupferdraht mit 10 mm Durchmesser und I = 100 A
Annahme: 1 Elektron pro Cu - Atom
Anzahl Cu - Atome pro Volumen
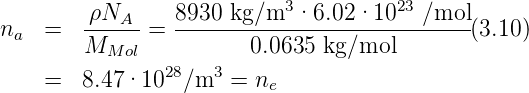
Und mit qk = e
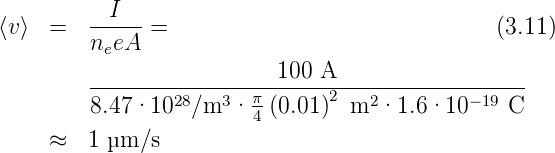
Mit v(t) = v0 cos(2πνt) und x(t) = ∫ v(t)dt hat man
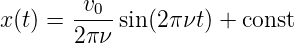
Die maximale Strecke erhält man wenn der Sinus von −1 nach +1 geht.
Folgerung: bei ν = 50 Hz Wechselstrom zittern die
Elektronen einige 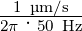 ·2 ≈ 6.4 nm weit.
·2 ≈ 6.4 nm weit.
__________________________________________________________________________
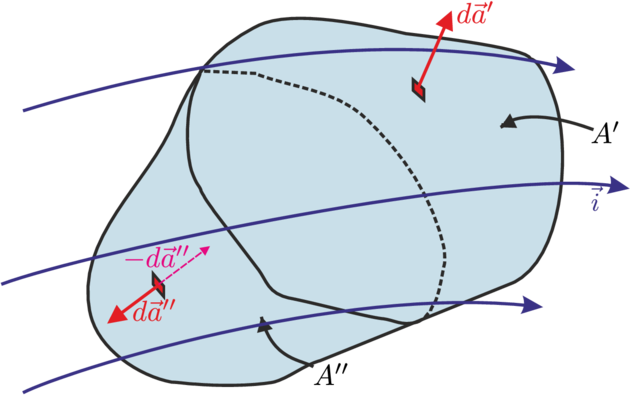
Berechnung des Flusses eines Stromdichtefeldes durch ein geschlossenes Gebiet
_____________________________________________________________________
Wir betrachten eine geschlossene Fläche A, die wir in zwei Teilflächen A′ und A′′ aufteilen, so dass auf der Fläche A′ die Feldlinie aus der Fläche austreten und auf der Fläche A′′ sie eindringen.
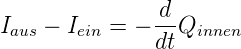 | (3.12) |
Wir schreiben die Gleichung mit der Stromdichte um
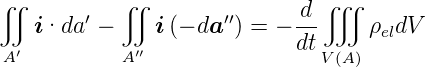 | (3.13) |
oder
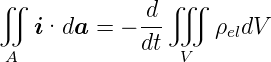 | (3.14) |
Dies ist die Integralform der Kontinuitätsgleichung.
Mit dem Gaussschen Satz bekommen wir
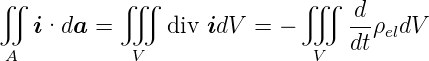 | (3.15) |
Die Differentialform der Kontinuitätsgleichung lautet demnach:
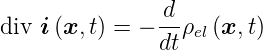 | (3.16) |
Bei stationären Strömen hängen 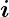 und ρel nicht von der
Zeit ab, so dass
und ρel nicht von der
Zeit ab, so dass
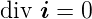 | (3.17) |
ist.
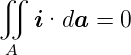 | (3.18) |
Beispiel:
________________________________________________________________
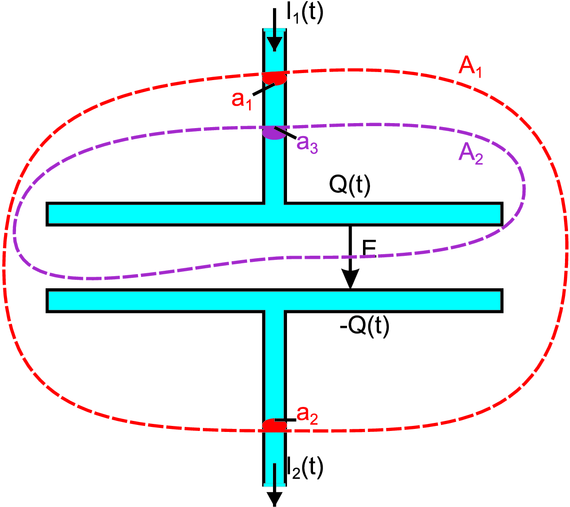
Stromfluss in einem Kondensator
_____________________________________________________________________
Wir betrachten eine quasistationäre Änderung am Kondensator
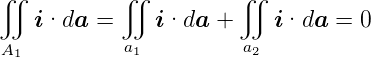 | (3.19) |
Mit I1 = −∬
a1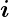 ·d
·d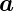 und I2 = ∬
a2
und I2 = ∬
a2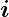 d
d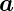 folgt
folgt
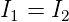 | (3.20) |
d.h. es scheint, als ob der Strom durch den Kondensator hindurch fliessen würde.
Wenn wir die Kontinuitätsgleichung auf A2 anwenden, bekommen wir
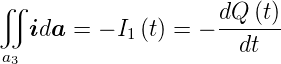 | (3.21) |
oder
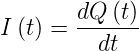 | (3.22) |
Die Einheit der Stromstärke ist Ampère ![[I ]](el-2017362x.png) = A
= A
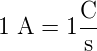 | (3.23) |
 Lizenzinformationen
Lizenzinformationen