__________________________________________________________________________
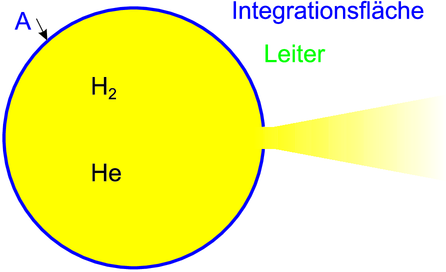
Metallischer Gastank mit Ausströmöffnung.
_____________________________________________________________________

(Siehe Tipler, Physik [TM04, pp. 812]) (Siehe Leisi, Klassische Physik II [Lei98, pp. 91])
Um die Magnetische Kraft zu berechnen gehen wir in zwei Schritten vor:
(Siehe Leisi, Klassische Physik II [Lei98, pp. 91])
__________________________________________________________________________

Metallischer Gastank mit Ausströmöffnung.
_____________________________________________________________________
Mit zwei Gedankenexperimenten soll geklärt werden, ob die Ladung von der Geschwindigkeit abhängt. Zuerst schliessen wir eine grosse Menge H2-Gas in den metallischen Tank ein, entladen ihn, und lassen das Gas ausströmen. Die Ladung des leeren Tanks ist unmessbar klein. Daraus schliesst man:
mit einer Genauigkeit von |
Dies folgt aus dem Gaussschen Gesetz Gleichung (2.3)
![∬ 1
E ·da = 0 ± a |qElektron| = -- [N Q (H2 ) + q]
A 𝜀0](el-2017474x.png) | (3.2) |
wobei q eine eventuell vor dem Ausströmen vorhandene Ladung, Q(H2) die Ladung eines Wasserstoffmoleküls und N die Anzahl der eingeschlossenen Wasserstoffmoleküle ist. a ist die Ungenauigkeit der Ladungsmessung. Aus der Tatsache, dass der Metallbehälter nach dem Ausströmen im Rahmen der Messgenauigkeit ungeladen ist, folgt, dass das H2-Molekül ungeladen ist.
Der Versuch wird mit He-Gas wiederholt. Das Resultat ist das gleiche. Nun bewegen sich aber die zwei Protonen im He-Atom mit sehr grosser Geschwindigkeit. Das bedeutet, dass die Ladung des Protons unabhängig von der Geschwindigkeit ist. Die Ladung muss insbesondere in jedem Inertialsystem gleich sein. Wir betrachten zwei Inertialsysteme S und S′5
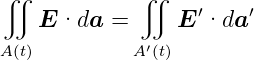 | (3.3) |
Diese Gleichung drückt die relativistische Ladungsinvarianz aus. Die Ladungsinvarianz ist nicht gleich der Ladungserhaltung. So ist zum Beispiel die Energie erhalten, zwischen zwei Inertialsystemen aber nicht invariant (m0c2 ⇔ m(v)c2).
(Siehe Leisi, Klassische Physik II [Lei98, pp. 94])
__________________________________________________________________________
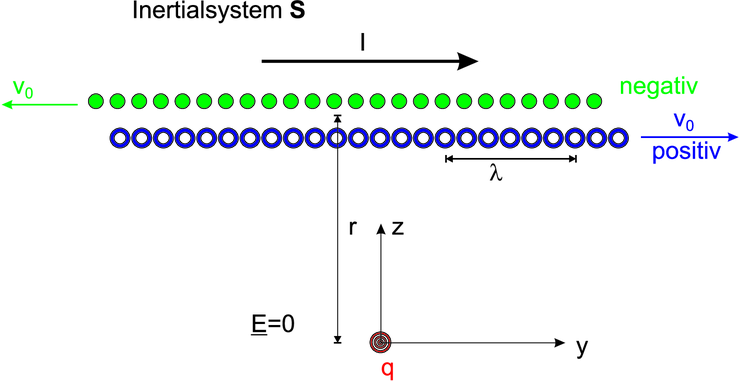
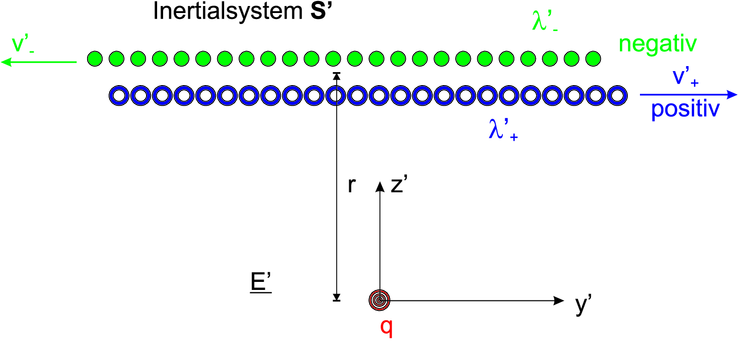
Berechnung der magnetischen Kraft. Links: im Bezugssystem S und rechts:im Bezugssystem S′, in dem q in Ruhe ist. Beachte: wir wissen zwar nicht, wie gross der Strom I gemessen im Bezugssystem S im Bezugssystem S′ ist. Die Ladung ist jedoch invariant.
_____________________________________________________________________
Den Strom I modellieren wir mit zwei Ketten aus Ladungsträgern, je eine positiv und negativ geladen. Ihre Linienladungsdichten λ sollen so sein, dass die beiden Ketten neutral sind. Im Ruhesystem S+ der positiven Ladungen ist
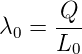 | (3.4) |
Im Inertialsystem S ist wegen der Ladungsinvarianz
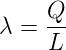 | (3.5) |
Wegen der Längenkontraktion gilt
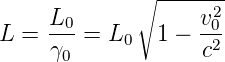 | (3.6) |
Zusammengenommen erhalten wir
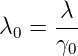 | (3.7) |
Die gleiche Beziehung kann für die negativen Ladungen
abgeleitet werden. Das heisst, wenn in S die Linienladungsdichten
der positiven und negativen Ladungen gleich sind, dann
auch in den jeweiligen Ruhesystemen. In den Ruhesystemen
ist die Linienladungsdichte geringer als in bewegten
Bezugssystemen. Da die beiden bewegten Ladungsketten
die gleiche Linienladungsdichte im System S haben, ist
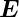 = 0.
= 0.
Im Ruhesystem S′, in dem das Teilchen mit der Ladung q in
Ruhe ist, sieht die Situation anders aus. Die Geschwindigkeit der
positiven und der negativen Ladungsketten ist unterschiedlich.
deshalb sind sie zusammen nicht mehr elektrisch neutral.
Auf die Ladung q wirkt eine elektrostatische Kraft. Da
die Relativgeschwindigkeit der positiven Ladungen zu
q kleiner ist als die der negativen Ladungen, liegen
in S′ die positiven Ladungen weniger dicht als die
negativen6 .
Die beiden Ladungsketten sind insgesamt negativ geladen.
Deshalb wird q angezogen, wenn q > 0 ist. Das 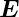 ′-Feld in die
z′-Richtung erzeugt in S′ die Kraft
′-Feld in die
z′-Richtung erzeugt in S′ die Kraft
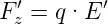 | (3.8) |
Das  -Feld hängt vom Bezugssystem ab, ist also
nicht relativistisch invariant! -Feld hängt vom Bezugssystem ab, ist also
nicht relativistisch invariant! |
Das elektrische Feld einer Linienladung im Abstand r ist
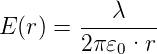 | (3.9) |
Um das elektrische Feld 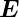 ′ berechnen wir die Geschwindigkeiten
v+′ und v−′ in S′.
′ berechnen wir die Geschwindigkeiten
v+′ und v−′ in S′.
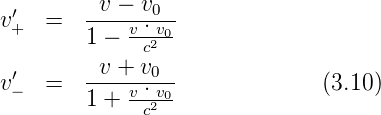
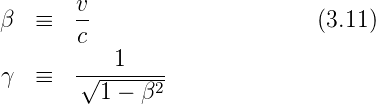
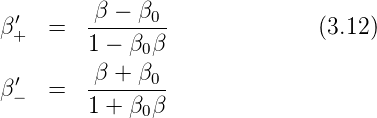
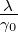 =
= 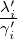 (i ∈{+,−}
(i ∈{+,−} 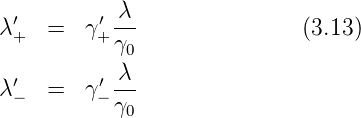
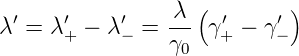 | (3.14) |
Weiter erhalten wir
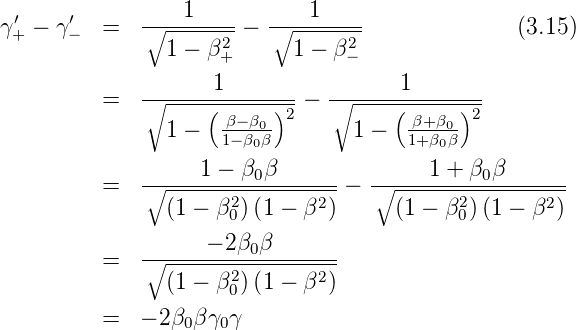
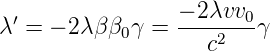 | (3.16) |
Betrachten wir am Ort der Ladung q das von der Linienladung λ′ hervorgerufene Feld Er′. Für positives λ′ zeigt dieses in die −z′-Richtung. Also ist das elektrische Feld
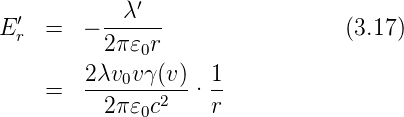
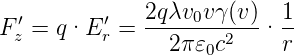 | (3.18) |
Wir verwenden die Lorentztransformation der Impulse pi und der Energie E
Der Vierervektor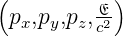 transformiert sich wie der
Vierervektor
transformiert sich wie der
Vierervektor 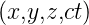 . Die Kraft transformiert sich also
wie
. Die Kraft transformiert sich also
wie
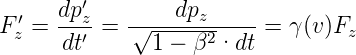 | (3.20) |
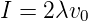 | (3.21) |
Damit bekommen wir
|
Multipliziert man Gleichung (3.22) mit der Dichte der Ladungsträger n (Einheit [n] = 1∕m), so erhält man die zu I2 proportionale Kraft pro Länge F(r).
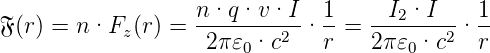 | (3.23) |
Aus F(r) bekommt man die Kraft auf ein Leiterstück der Länge ℓ
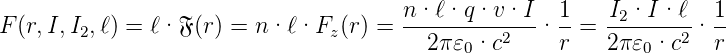 | (3.24) |
In der Gleichung (3.24) können wir die Terme so sortieren, dass ein Leiter als Ursache eines Feldes und der Rest als Wirkung dasteht, analog wie beim elektrischen Feld.
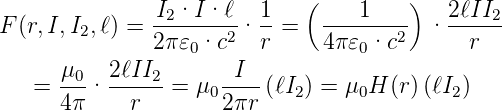 | (3.25) |
Wir haben den Vorfaktor zur Permeabilität des Vakuums zusammengefasst mit
![1 −2
μ0 = 𝜀-c2 [μ0] = NA
0](el-2017506x.png) | (3.26) |
Der Zahlenwert der Permeabilität des Vakuums ist im SI-System zur Definition des Ampères vorgegeben
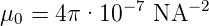 | (3.27) |
Die Funktion
![H (r) = -I-- [H (r)] = Am −1
2πr](el-2017508x.png) | (3.28) |
ist das magnetische Feld. Es hat für den Magnetismus die gleiche Funktion wie das elektrische Feld.
 Lizenzinformationen
Lizenzinformationen