 -Feld
-Feld
 -Feld
-Feld
__________________________________________________________________________
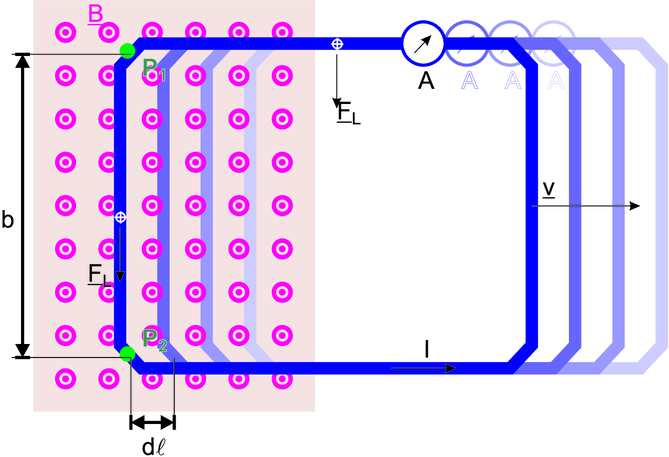
Induktion eines Stromes in einer in einer inhomogenen magnetischen Induktion bewegten Leiterschlaufe.
_____________________________________________________________________
Wir bewegen eine Leiterschlaufe mit der Geschwindigkeit 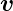 aus
dem begrenzten Gebiet mit einer homogenen magnetischen
Induktion heraus. Auf die beweglichen Ladungsträger, hier
positiv angenommen, wirkt die Lorentzkraft
aus
dem begrenzten Gebiet mit einer homogenen magnetischen
Induktion heraus. Auf die beweglichen Ladungsträger, hier
positiv angenommen, wirkt die Lorentzkraft 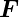 L. Auf den
horizontalen Teilen der Leiterschlaufe kennen wir den
Effekt: eine Hallspannung (Siehe Abschnitt 3.9) auf. Im
vertikalen Teil im Magnetfeld bewirkt die Hallspannung eine
Beschleunigung der Ladungsträger. Nach der Definition der
elektromotorischen Kraft (Siehe Gleichung (3.9)) haben
wir
L. Auf den
horizontalen Teilen der Leiterschlaufe kennen wir den
Effekt: eine Hallspannung (Siehe Abschnitt 3.9) auf. Im
vertikalen Teil im Magnetfeld bewirkt die Hallspannung eine
Beschleunigung der Ladungsträger. Nach der Definition der
elektromotorischen Kraft (Siehe Gleichung (3.9)) haben
wir
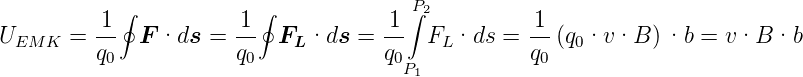 | (4.1) |
Hat die Drahtschlaufe den Widerstand R, so fliesst der Strom
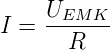 | (4.2) |
| Versuch zur Vorlesung: | |
| Induktion (Versuchskarte EM025) | |
| Versuch zur Vorlesung: | |
| Induktion im Erdfeld (Versuchskarte EM027) | |
(Siehe Leisi, Klassische Physik II [Lei98, pp. 138]) (Siehe Tipler, Physik [TM04, pp. 876])
Im Zusammenhang mit den elektrischen Feldern 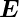 hatten wir den elektrischen Fluss ϕE (Siehe Abschnitt 2.3)
eingeführt. Hier bewegen wir die Leiterschlaufe mit der
Geschwindigkeit
hatten wir den elektrischen Fluss ϕE (Siehe Abschnitt 2.3)
eingeführt. Hier bewegen wir die Leiterschlaufe mit der
Geschwindigkeit 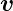 , wir ändern damit die vom Magnetfeld
durchflossene Fläche A um die Grösse da = −dℓ·b. Da die
Geschwindigkeit v = dℓ∕dt ist, können wir auch schreiben
, wir ändern damit die vom Magnetfeld
durchflossene Fläche A um die Grösse da = −dℓ·b. Da die
Geschwindigkeit v = dℓ∕dt ist, können wir auch schreiben
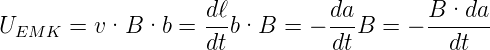 | (4.3) |
schreiben. Wir definieren den
magnetischen Fluss
durch die von der geschlossenen Kurve S berandete Fläche A |
Damit ist die induzierte EMK
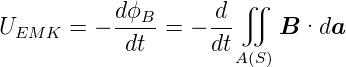 | (4.5) |
Sie wird durch den zeitlich sich ändernden Fluss erzeugt.
Die Einheit des magnetischen Flusses ist Weber.
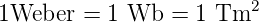 | (4.6) |
Das Minuszeichen in den Gleichungen für den magnetischen Fluss rührt daher, dass eine Geschwindigkeit in die positive x-Richtung eine Verkleinerung der Fläche A bewirkt.
Das durch den Strom erzeugte Magnetfeld ist so gerichtet, dass die Bewegung der Spule gebremst wird. Dieses Verhalten wird in der Lenzschen Regel zusammengefasst:
| Die Induktionsspannung und der Strom, den sie bewirkt, sind stets so gerichtet, dass sie der Ursache entgegenwirken. |
________________________________________________________________
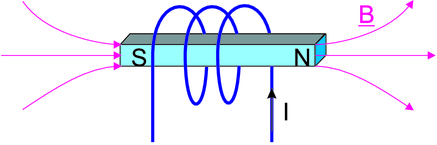
Vergleich eines Stabmagneten mit einer Spule. Der magnetische Nordpol ist üblicherweise rot, der Südpol grün markiert.
_____________________________________________________________________
Eine Spule erzeugt ein axiales Magnetfeld. Die Richtung des Magnetfeldes wird mit der Rechten Hand-Regel aus der Stromrichtung abgeleitet. Ein Stabmagnet erzeugt ein gleiches Magnetfeld wie eine Spule.
Die Nord- und Südpole der Magnete sind so
definiert: Die  -Feldlinien laufen vom Nordpol zum
Südpol. Der Nordpol ist rot markiert, der Südpol
grün. -Feldlinien laufen vom Nordpol zum
Südpol. Der Nordpol ist rot markiert, der Südpol
grün. |
________________________________________________________________
________________________________________________________________
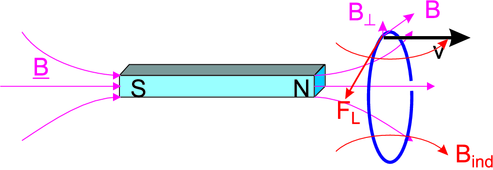
Bewegt man einen Magneten mit der Geschwindigkeit 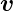 von
einem Stabmagneten weg, so bewirkt die Lorentzkraft
einen Strom I, der ein Magnetfeld
von
einem Stabmagneten weg, so bewirkt die Lorentzkraft
einen Strom I, der ein Magnetfeld 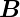 ind induziert. Dieses
Magnetfeld ist so gerichtet, dass es gleichsinnig wie das
Magnetfeld des Stabes ist. Der Metallring wird also vom
Stabmagneten angezogen und in seiner Bewegung nach rechts
gebremst (Lenzsche Regel).
ind induziert. Dieses
Magnetfeld ist so gerichtet, dass es gleichsinnig wie das
Magnetfeld des Stabes ist. Der Metallring wird also vom
Stabmagneten angezogen und in seiner Bewegung nach rechts
gebremst (Lenzsche Regel).
__________________________________________________________________________
_____________________________________________________________________
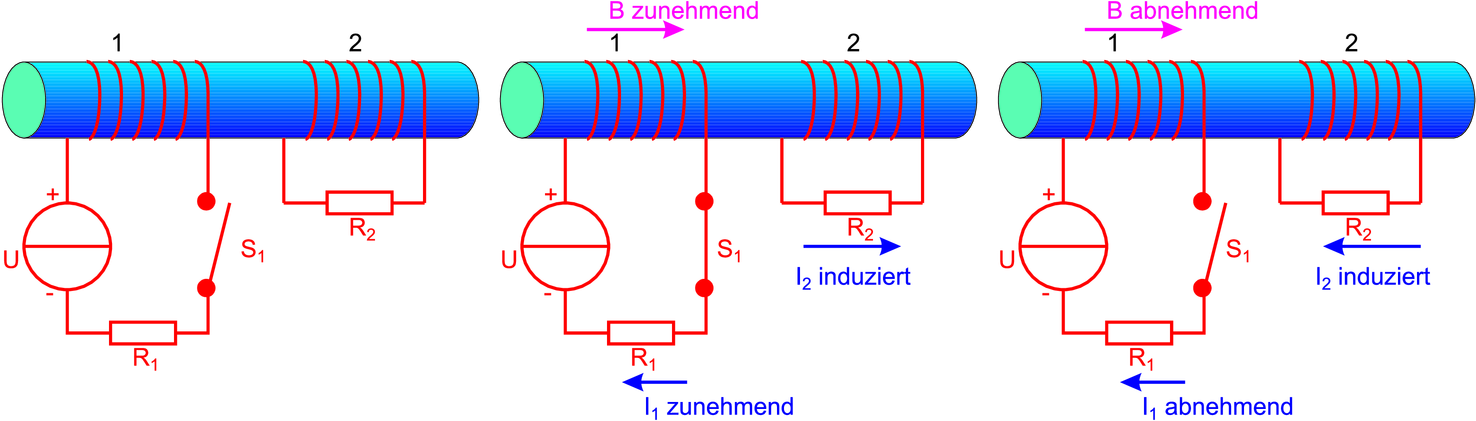
Hier wird ein Magnetfeld eingeschaltet. Die Richtung der Feldlinien wird durch die Rechte-Hand-Regel bestimmt. Ein zeitlich zunehmendes Magnetfeld in der rechten Spule ist äquivalent zu einer Bewegung der rechten Spule im inhomogenen Feld (links intensiver als rechts) nach links. Dabei zeigt die relevante Feldkomponente nach aussen. Aus der Rechten Hand-Regel ergibt sich die angegebene Stromrichtung. Nach dem Ausschalten des erregenden Stromes nimmt die Intensität des Magnetfeldes ab. Dies ist äquivalent zu einer Bewegung der rechten Spule nach rechts, bei gleichbleibender Richtung des Magnetfeldes. Entsprechend dreht sich die Richtung des Stromes um.
__________________________________________________________________________
________________________________________________________________
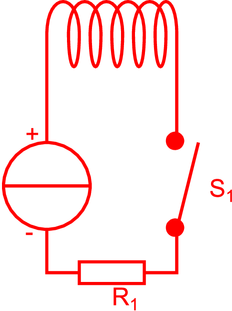
Wenn eine Spule von einem Strom durchflossen ist, wird dadurch ein Magnetfeld erzeugt. Wenn nun der Strom durch die Spule geändert wird, wird eine Spannung induziert, die wie im vorigen Falle so gerichtet ist, dass sie der Änderung des Magnetfeldes entgegenwirkt, so also auch der Änderung des durch die Spule fliessenden Stromes. Im besonderen Falle, dass der Strom abgeschaltet wird, dass also der Widerstand im Stromkreis um viele Grössenordnungen steigt, bildet sich eine sehr hohe Spannung.
Anwendungen
| Versuch zur Vorlesung: | |
| Tesla-Transformator (Versuchskarte EM064) | |
| Folien zur Vorlesung vom 18. 06. 2009: PDF | |
| Aufgabenblatt 10 für das Seminar vom 24. 06. 2009 (Ausgabedatum 18. 06. 2009): (HTML oder PDF) | |
Wir betrachten die Situation in der Abbildung 4.1.1 im Ruhesystem S′ der Schleife. Im Laborsystem S ist das Magnetfeld
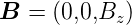
in die z-Richtung gerichtet. Die Geschwindigkeit zeigt in die y-Richtung. Mit der Lorentztransformation (3.21) berechnen wir die Felder im System S′. Wir erhalten
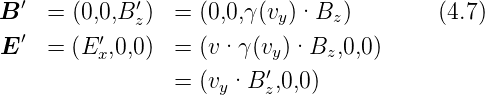
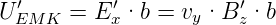 | (4.8) |
Die Flussänderung ist
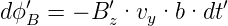 | (4.9) |
Somit lauten das Induktionsgesetz und das Ohmsche Gesetz
Somit gilt für die EMK die Transformation
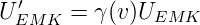 | (4.11) |
Die Gleichungen (4.11) gelten in jedem Falle. Wenn v « c
ist, kann man die Unterschiede im Strom I, in der EMK
UEMK und im Magnetfeld 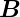 vernachlässigen.
vernachlässigen.
Die Transformationseigenschaften zeigen, dass das
Induktionsgesetz auch bei stationären Leiterschleifen und
zeitlich ändernden Magnetfeldern gelten muss (wir begeben
uns in das System S′). Die Wirkungen der Felder 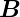 und
und 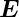 sind unabhängig von ihrer Entstehung.
sind unabhängig von ihrer Entstehung.
| Versuch zur Vorlesung: | |
| Magnetische Induktion (Versuchskarte EM051) | |
Für einen beliebig geformten ruhenden Leiter (gegeben durch die Kurve S) in einem zeitlich ändernden Magnetfeld gilt für die EMK
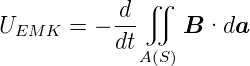 | (4.12) |
Da der Leiter in Ruhe ist, muss die EMK durch ein elektrisches Feld erzeugt sein.
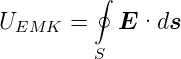 | (4.13) |
und damit
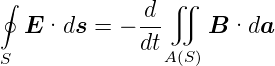 | (4.14) |
Bei einer bewegten Leiterschlaufe kann der magnetische Fluss sich ändern,
Für eine bewegte Leiterschlaufe muss das elektrische Feld 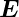 ′ im
bewegten Bezugssystem und die magnetische Induktion
′ im
bewegten Bezugssystem und die magnetische Induktion 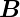 im
Laborsystem berechnet werden[Jac75, p. 210]. d
im
Laborsystem berechnet werden[Jac75, p. 210]. d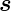 ′ ist das
Linienelement im Ruhesystem, in dem
′ ist das
Linienelement im Ruhesystem, in dem 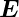 ′ gemessen wird. Wir
erhalten
′ gemessen wird. Wir
erhalten
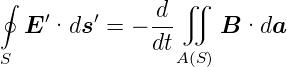 | (4.15) |
Mit der Gleichung(C.40) für die Beziehung zwischen zeitlichen Ableitungen in Ruhesystemen und mitgeführten Systemen und dem Satz von Stokes (Siehe Gleichung (C.1)) erhalten wir
![∮ ∬
U′ = E ′·ds ′ = −-d B ·da
EMK dt
S[ A(S) ]
∬ -∂-
= − ∂t B + rot (B × v) ·da
A(S)
∬ ∂ ∮ ′
= − --B ·da − (B × v )·ds
A (S) ∂t S](el-2017835x.png) | (4.16) |
Dies kann auch so geschrieben werden:
![∮ ∬
[E ′ + (B × v)]·ds ′ = − -∂B ·da
∂t
S A(S)](el-2017836x.png) | (4.17) |
Wenn man sich nach Jackson [Jac75, p. 212] alternativ vorstellt, dass der Weg S zu einem Zeitpunkt fix im Raum ist, gilt auch
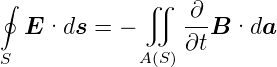 | (4.18) |
Deshalb erhalten wir für das elektrische Feld 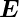 im
Laborsystem
im
Laborsystem
![∮ ∮
[E ′ + (B × v )]·ds ′ = E ·ds
S S](el-2017839x.png) | (4.19) |
Bei kleinen Geschwindigkeiten ist d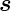 = d
= d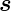 ′.
′.
Damit ist
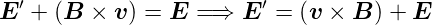 | (4.20) |
Weiter kann man daraus die Lorentzkraft ablesen:
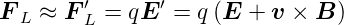 | (4.21) |
Zurück zum Faradayschen Induktionsgesetz: Mit Gleichung
(4.20) kann in Gleichung (4.17) 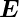 ′ eliminiert werden.
Das universelle Induktionsgesetz von Faraday
lautet
′ eliminiert werden.
Das universelle Induktionsgesetz von Faraday
lautet
|
Mit dem Satz von Stokes (Siehe Gleichung (C.1)) erhält man
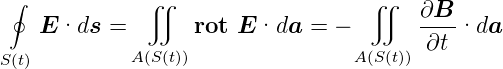 | (4.23) |
Für zeitunabhängige Berandungen A(S) darf man Ableitung und Integral nicht vertauschen. Das Induktionsgesetz lautet dann
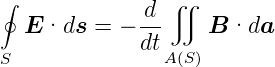 |
Da diese Integralgleichung für beliebige Kurven S gelten muss, also auch für infinitesimal kleine, erhalten wir die differentielle Form des Faradayschen Induktionsgesetzes
|
Bei der Ableitung des Faradayschen Induktionsgesetzes haben wir von der Kleinheit der Geschwindigkeiten Gebrauch gemacht, explizit und implizit. Eine relativistisch korrekte Rechnung führt auf die gleichen Ergebnisse.
| Versuch zur Vorlesung: | |
| Fallrohre (Versuchskarte EM057) | |
_______________________________________________
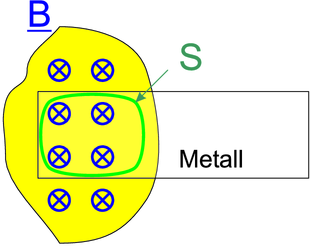
_____________________________________________________________________
Wenn sich ein Metallstück in einem inhomogenen Magnetfeld befindet, dann muss für jede Bahnkurve S das Faradaysche Induktionsgesetz gelten. Da der Leiter einen spezifischen Widerstand ρel hat, fliesst bei einer Änderung des Flusses durch S, zum Beispiel, indem man den Leiter bewegt, ein durch die induzierte Spannung getriebener Strom. Die Richtung des Stromes ist so, dass er sich einer Änderung des magnetischen Flusses widersetzt. Bei einem perfekten Leiter, müssten enorm grosse Kräfte aufgebracht werden, um das Metallstück mit einer minimalen Geschwindigkeit bewegen zu können. Durch die Dissipation im Ohmschen Leiter wird der induzierte Strom geschwächt, so dass die der Bewegung entgegengesetzte Kraft umso kleiner ist, je schlechter die Leitfähigkeit des Metalls ist.
Um die Grössenordnung des Wirbelstromes abzuschätzen betrachten wir lokal ein Stück Metall das mit der Geschwindigkeit vy durch eine magnetische Induktion in die x- Richtung, Bx, gezogen wird. Wir betrachten die Felder im Ruhesystem der Platte. Aus den Lorentz-Transformationen erhalten wir
da v2∕c2 « 1 ist. Lokal gilt der Zusammenhang
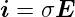 | (4.26) |
Weiter können wir aus P = IU mit i = I∕A und Ez′ = U∕d und der Bezeichnung für das Volumen V = Ad schreiben
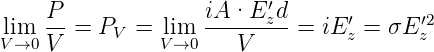 | (4.27) |
Andererseits hängt die dissipierte Leistung pro Volumen von der Volumenkraft FV und der Geschwindigkeit vy ab.
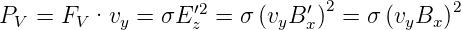 | (4.28) |
Die Volumenkraft ist also
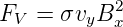 | (4.29) |
Die Berechnung wurde anhand eines unendlich ausgedehnten Leiters in einem Magnetfeld gemacht. Endliche Leiter und endliche Magnetfelder bewirken, dass der Effekt nur an den Grenzen vorhanden ist.
__________________________________________________________________________
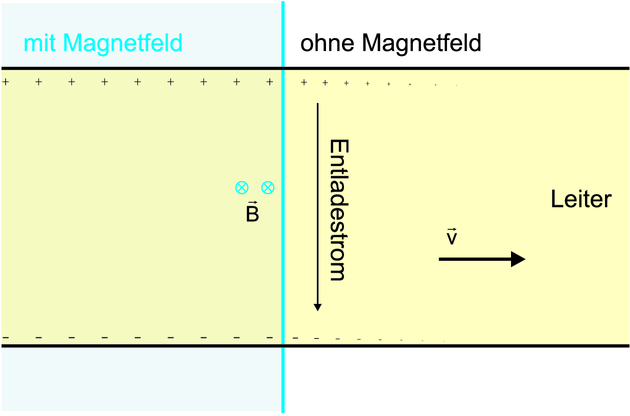
Bewegung eines Leiters aus einem Magnetfeld.
_____________________________________________________________________
Im Ruhesystem des Leiters bewirkt das elektrische Feld eine Bewegung der Ladungsträger an die Seiten des Leiters (analog wie beim Halleffekt). Dadurch wird ein Gegenfeld aufgebaut, bis die Bewegung der Ladungsträger zum Erliegen kommt (Siehe Abbildung 4.1.4, linke Seite). Wenn der Leiter den Bereich des Magnetfeldes verlässt (wir nehmen eine scharfe Grenze an, dann gleichen sich die Ladungen aus. Die Ströme erzeugen wegen der endlichen Leitfähigkeit σ eine Wärmeleistung, das heisst es gibt eine Gegenkraft. Kondensatoren werden exponentiell entladen, so dass die Wirkung des ändernden Feldes lokal begrenzt ist. Auf der anderen Seite des Magnetfeldes tauchen die gleichen Effekte auf, aber beim Laden des Kondensators. Auch dort nimmt der Strom exponentiell ab beim Entfernen von der Grenze. Warum heisst es dann doch Wirbelströme? Wir haben einen Stromkreis, bei dem die magnetische Induktion die elektromotorische Kraft bewirkt (wie beim van de Graaff-Generator). Während im Ruhesystem des Leiters die Effekte durch das elektrische Feld erklärt werden, müssen sie im Laborsystem mit Flussänderung und magnetischer Induktion beschrieben werden.
In Transformatoren ist die magnetische Induktion parallel zum Eisen, die Wirbelströme transversal dazu. Die Wirbelströme können vermindert werden, indem das Metall geschlitzt wird oder in Lagen mit Isolatoren dazwischen gebündelt wird.
Anwendungen
Beispielswerte
_________________________________________________________________
| Cu | Al | Fe | Ti | Gd
| ||||||
| B∕T → | 0.1 | 1 | 0.1 | 1 | 0.1 | 1 | 0.1 | 1 | 0.1 | 1 |
| v∕(m/s) | ||||||||||
| 0.01 | 5.8·10−5 | 5.8·10−3 | 3.7·10−5 | 3.7·10−3 | 0.00001 | 0.001 | 2.56·10−6 | 0.000256 | 7.40·10−7 | 0.000074 |
| 0.1 | 5.8·10−4 | 5.8·10−2 | 3.7·10−4 | 3.7·10−2 | 0.0001 | 0.01 | 0.0000256 | 0.00256 | 7.40·10−6 | 0.00074 |
| 1 | 5.8·10−3 | 5.8·10−1 | 3.7·10−3 | 0.37 | 0.001 | 0.1 | 0.000256 | 0.0256 | 0.000074 | 0.0074 |
| 10 | 5.8·10−2 | 5.8 | 3.7·10−2 | 3.7 | 0.01 | 1. | 0.00256 | 0.256 | 0.00074 | 0.074 |
__________________________________________________________________________________________________________________
Eine unendlich lange Spule kann man sich aus kreisförmigen Leitern zusammengesetzt denken.
__________________________________________________________________________
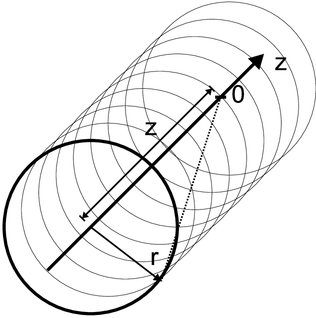
Die magnetische Induktion am Punkt 0 auf der z-Achse kann berechnet werden, indem mit Gleichung (3.54) die magnetische Induktion eines Rings mit der Stromdichte I·n·dz berechnet wird und dann über alle Ringströme addiert wird.
_____________________________________________________________________
Wir berechnen zuerst die magnetische Induktion eines
Kreisringes mit dem Radius r im Abstand z vom Nullpunkt
(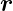 ′ = (x,y,z)) am Nullpunkt (
′ = (x,y,z)) am Nullpunkt (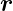 = (0, 0, 0)). Ausgehend von
Gleichung (3.54) schreiben wir für einen Kreisring auf der
Position z mit dem Radius r für
= (0, 0, 0)). Ausgehend von
Gleichung (3.54) schreiben wir für einen Kreisring auf der
Position z mit dem Radius r für 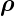 .
.
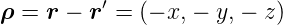
Da r konstant ist, schreiben wir x und y als Funktion des Winkels ϕ
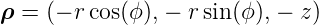
Der Strom I soll im Gegenuhrzeigersinn umlaufen, also in positiver Richtung. Ein Längenelement entlang des Kreisringes ist
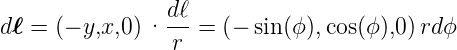
Das Vektorprodukt d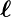 ×
×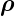 ergibt
ergibt
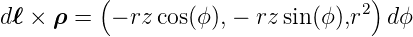
Mit dem Strom pro Windung I wird die magnetische
Induktion am Punkte 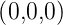
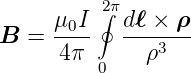 |
Die x- und die y-Komponenten von d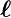 ×
×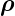 enthalten eine
Winkelfunktion zur ersten Potenz und ergeben bei einer
Integration von 0 nach 2π null. Die z-Komponente der
magnetischen Induktion ist
enthalten eine
Winkelfunktion zur ersten Potenz und ergeben bei einer
Integration von 0 nach 2π null. Die z-Komponente der
magnetischen Induktion ist
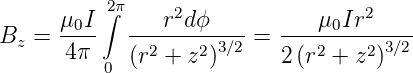 | (4.30) |
Die magnetische Induktion einer unendlich langen Spule bekommt man, indem wir den Strom I durch das Produkt aus Strom I, der Windungszahl pro Länge (Windungsdichte) n und dem Längenelement dz ersetzen und integrieren.
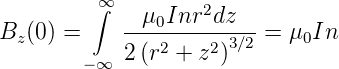 | (4.31) |
Wird die unendlich lange Spule bei z = 0 geteilt, tragen beide Spulenhälften gleichviel zur magnetischen Induktion bei z = 0 bei. Wird nun eine Hälfte entfernt, so ist die magnetische Induktion auf der Spulenachse
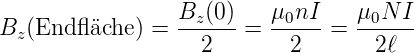 | (4.32) |
Endlich lange Spulen der Länge ℓ » r verhalten sich wie unendlich lange Spulen. Wenn sich auf der Länge ℓ N Windungen befinden, haben wir
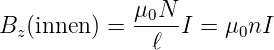 | (4.33) |
Der magnetische Fluss in einer Spule entsteht durch Ströme in dieser Spule selber, oder in anderen Spulen. Nach dem Gesetz von Laplace oder Biot-Savart (Siehe Gleichung (3.54)) ist die magnetische Induktion proportional zum Strom. Somit ist auch der Fluss ϕB proportional zum Strom. Diese Proportionalität wird mit
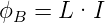 | (4.34) |
ausgedrückt, wobei L die Selbstinduktivität der Spule ist.
Die Einheit der Induktivität ist
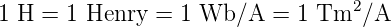
| Folien zur Vorlesung vom 22. 06. 2009: PDF | |
In den meisten Fällen ist es schwierig, die Selbstinduktivität einer Schaltung zu berechnen. Für eine lange, dicht gewickelte Spule ergibt Gleichung (4.33) die magnetische Induktion
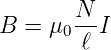 | (4.35) |
Dabei ist N = n·ℓ die Anzahl Windungen auf der Länge ℓ. Die magnetische Induktion B hängt von der Dichte der Windungen ab, nicht aber von der Länge der Spule. Hat die Spule den Querschnitt A, so ist der Fluss
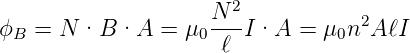 | (4.36) |
Damit ist die Induktivität der Spule
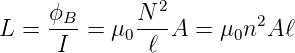 | (4.37) |
Die magnetische Permeabilität μ0 kann also auch als
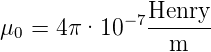 | (4.38) |
Die Änderung der Stromstärke bedingt eine Änderung des magnetischen Flusses.
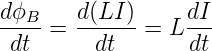 | (4.39) |
Somit wird mit Gleichung (4.5)
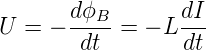 | (4.40) |
Mit dieser Gleichung wird die Funktionsweise des Funkeninduktors klar.
| Versuch zur Vorlesung: | |
| Funkeninduktor (Versuchskarte EM017) | |
_______________________________________________
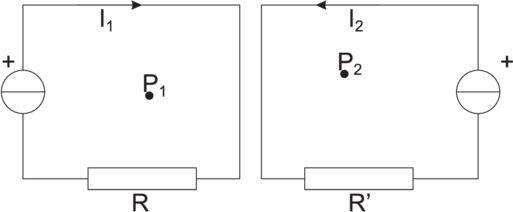
Zwei gekoppelte Stromkreise
_____________________________________________________________________
Der magnetische Fluss am Punkt P2 hängt sowohl vom Strom I2 wie auch vom Strom I1 ab:
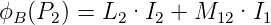 | (4.41) |
Ebenso hängt der magnetische Fluss am Punkt P1 von beiden Strömen ab
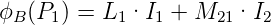 | (4.42) |
Neben der Selbstinduktivität Li müssen bei realen Systemen auch die Gegeninduktivitäten Mij berücksichtigt werden. Wie bei den Induktivitäten hängt auch bei den Gegeninduktivitäten die Grösse allein von der Geometrie ab.
__________________________________________________________________________
________________________________________________________________
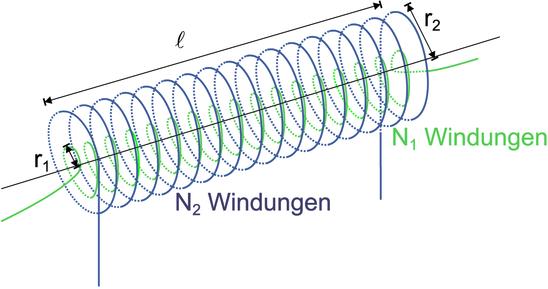
Im allgemeinen ist es schwierig, die Gegeninduktivitäten zu berechnen. Bei zwei ineinander gewickelten Spulen, einem Beispiel für einen Transformator, gelingt dies. Wir wollen das Beispiel verwenden, um zu zeigen, dass M12 = M21 ist. Durch die Spule 1 (Länge ℓ, Radius r1, Windungsdichte n1 = N1∕ℓ) fliesst der Strom I1, durch die zweite Spule 2 (Länge ℓ, Radius r2, Windungsdichte n2 = N2∕ℓ) soll der Strom I2 fliessen. Da wir lange Spulen betrachten, ist das Magnetfeld im Inneren der Spulen homogen. Also ist
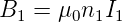 | (4.43) |
Ausserhalb der Spule 1 ist das Magnetfeld B1 = 0 (Annahme einer langen Spule). Deshalb ist der Fluss durch den Strom I1 für die Spule 2 gegeben durch
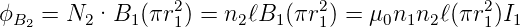 | (4.44) |
Die Gegeninduktivität M12 ist also
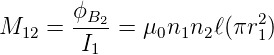 | (4.45) |
Im entgegengesetzten Falle beginnen wir mit
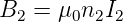 | (4.46) |
Der für die Spule 1 relevante Fluss ist durch die von der Spule 1 umschlossene Fläche, also N1(πr12) gegeben.
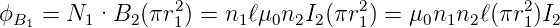 | (4.47) |
Damit wird die Gegeninduktivität
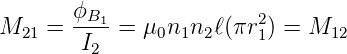 | (4.48) |
Diese Beziehung, die an einem Spezialfall gezeigt wurde, gilt auch allgemein (ohne Beweis).
__________________________________________________________________________
________________________________________________________________
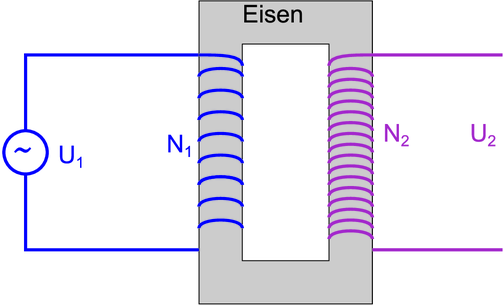
Die in einem Transformator induzierte Spannung kann wie folgt berechnet werden. In der Spule 1 fällt die Spannung
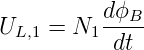 | (4.49) |
ab. Diese Spannung muss durch die Wechselspannungsquelle U erzeugt werden, so das
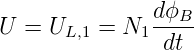 | (4.50) |
ist. Durch die Anordnung des Eisens wird erreicht, dass der gesamte durch die erste Spule erzeugte magnetische Fluss durch die zweite Spule fliesst. Dort haben wir die induzierte Spannung
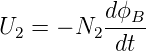 | (4.51) |
und somit
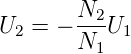 | (4.52) |
N2∕N1 heisst der Übersetzungsfaktor des Transformators.
Wird der Ausgang des Transformators mit dem Ohmschen Widerstand R belastet, fliesst der Strom I2, der zu U2 in Phase ist. Dieser Strom erzeugt einen magnetischen Fluss ϕB′ ∝ N2I2, der den ursprünglichen Fluss ϕB durch die Spule 2 schwächt. Da durch beide Spulen der gleiche magnetische Fluss fliesst, muss auch der Fluss durch die erste Spule geschwächt werden. Da die Spannung durch die Spannungsquelle U vorgegeben ist, muss der Strom I1 auf der Primärseite zusätzlich fliessen, so dass ϕB′∝ N1I1 gilt. Da die Proportionalitätsfaktoren bis auf das Vorzeichen gleich sind, gilt dann auch
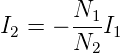 | (4.53) |
Wenn wir die Effektivwerte betrachten haben wir damit
![[ ][ ]
U I = − N2-U − N1-I = U I
2 2 N1 1 N2 1 1 1](el-2017892x.png) | (4.54) |
sofern man Verluste vernachlässigt. Ideale Transformatoren übertragen also verlustfrei Leistung.
| Versuch zur Vorlesung: | |
| Hochspannungsleitung (Versuchskarte EM161) | |
| Versuch zur Vorlesung: | |
| Transformatorenversuche (Versuchskarte EM066) | |
__________________________________________________________________________
_____________________________________________________________________
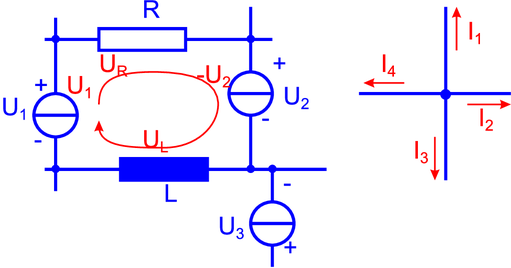
In einer komplizierten elektrischen Schaltung betrachtet man eine einzelne Masche. Nach der Definition der EMK muss eine Probeladung langsam um die Masche herumgeführt werden. Dies führt auf die Maschenregel
|
wobei die Vorzeichen entsprechend dem Umlaufsinn einzusetzen sind. In unserem Beispiel bedeutet dies:
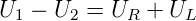
Die Knotenregel ist ein Ausdruck für die Ladungserhaltung. Wenn wir zum Beispiel alle zufliessenden Ströme positiv und alle wegfliessenden Ströme negativ zählen (oder umgekehrt), gilt an jedem Knoten
|
Mit diesen beiden Regeln sowie der Kenntnis der Charakteristika der Bauelemente kann jede statische oder quasistatische elektronische Schaltung berechnet werden.
In diesem Abschnitt betrachten wir die Wirkung von cosinusförmigen Wechselspannungen
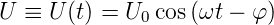 | (4.57) |
Die Zeitskala für die Wechselspannung wird so gewählt, dass φ = 0 ist. Weiter setzen wir voraus, dass die zeitliche Änderung aller Grössen so gering sind, dass wir wie im stationären Falle rechnen können. Wir dies den quasistationären Fall.
__________________________________________________________________________
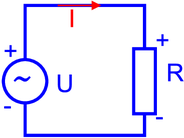
Definition von Strömen und Spannungen bei Wechselspannungen
_____________________________________________________________________
Da bei Wechselspannungen a priori keine Stromrichtung vorgegeben ist, definiert man, zum Beispiel wie in der Abbildung oben, die Stromrichtung zu einem bestimmten Zeitpunkt, hier für t = 0. Zu jedem Zeitpunkt muss die Spannung im Stromkreis insgesamt null sein. Also ist
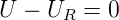 | (4.58) |
und mit dem Ohmschen Gesetz
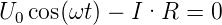 | (4.59) |
oder
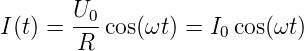 | (4.60) |
Der Strom und die Spannung erreichen immer dann einen Extremwert, wenn ωt ein ganzzahliges Vielfaches von π ist. Der durch einen Widerstand fliessende Strom ist in Phase mit der Spannung.
Die momentane Leistung am Widerstand ist
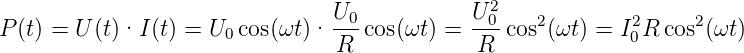 | (4.61) |
Der Mittelwert der Leistung ist (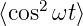 t = 1∕2)
t = 1∕2)
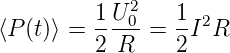 | (4.62) |
Unter dem Effektivwert der Spannung (des Stromes) versteht man diejenige Gleichspannung, die an einem Ohmschen Widerstand die gleiche Verlustleistung erzeugt. Also ist für sinusförmige Spannungen
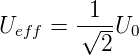 | (4.63) |
beziehungsweise
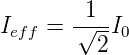 | (4.64) |
Für beliebige Spannungsverläufe (Stromverläufe) ist der Effektivwert (auch rms-Wert von ”Root Mean Square”)
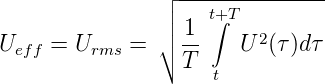 | (4.65) |
wobei T eine Zeit ist, die bei periodischen Signalen der Periodendauer entspricht und bei zufälligen Signalen lang gegenüber der charakteristischen Zeitdauer der Schwankungen sein muss. Für Ströme gilt die analoge Formel
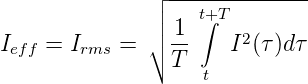 | (4.66) |
| Versuch zur Vorlesung: | |
| Wechselstromwiderstand (Versuchskarte EM053) | |
| Folien zur Vorlesung vom 25. 06. 2009: PDF | |
| Aufgabenblatt 11 für das Seminar vom 01. 07. 2009 (Ausgabedatum 25. 06. 2009): (HTML oder PDF) | |
_______________________________________________
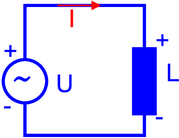
Spule mit Wechselspannung
_____________________________________________________________________
Wir verwenden Gleichung (4.40) um die Spannung über der Spule zu berechnen. Die induzierte Spannung ist der Flussänderung entgegengesetzt. Sie wirkt so, dass die Zunahme des Stromes bei zunehmender Anregungsspannung gebremst wird. Deshalb ist
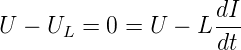 | (4.67) |
Setzen wir U = U0 cos(ωt) ein, erhalten wir
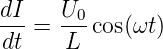 | (4.68) |
und damit
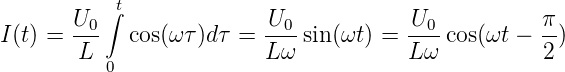 | (4.69) |
Der Strom hat also den Scheitelwert
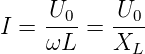 | (4.70) |
wobei XL = ωL die Impedanz oder der induktive Widerstand der Spule ist. Die Einheit der Impedanz ist gleich wie die Einheit des Widerstandes, das Ohm. Der Strom folgt der Spannung mit einer Phasenverschiebung von −π∕2. Für die Effektivwerte gilt Ieff = Ueff∕XL, da für sinusförmige Spannungen und Ströme der gleiche Faktor zur Umrechnung von Scheitelwerten zu Effektivwerten verwendet werden muss.
Die momentan dissipierte Leistung an einer Spule ist
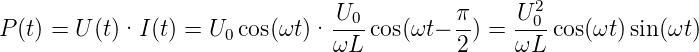 | (4.71) |
Die dissipierte Leistung kann sowohl positiv wie auch negativ sein. Die mittlere dissipierte Leistung ist
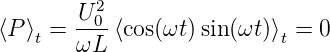 | (4.72) |
Im Mittel wird also keine Leistung an einer Spule dissipiert.
__________________________________________________________________________
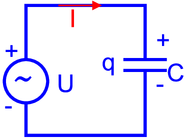
Kondensator mit Wechselspannung
_____________________________________________________________________
Beim Kondensator ist UC = q∕C. Diese Spannung muss gleich der treibenden Spannung sein.
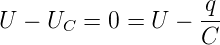 | (4.73) |
Wir setzen U ein und erhalten
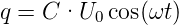 | (4.74) |
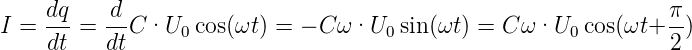 | (4.75) |
Wir nennen
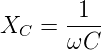 | (4.76) |
die Impedanz des Kondensators. Der Scheitelwert des Stromes ist
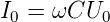 | (4.77) |
Analog wie bei der Spule gilt die Gleichung Ieff = Ueff∕XC mit der gleichen Begründung auch für Kondensatoren. Die momentan dissipierte Leistung ist
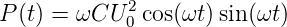 | (4.78) |
Sie ist, analog wie bei der Spule, positiv oder negativ. Deshalb ist die mittlere dissipierte Leistung
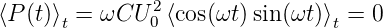 | (4.79) |
| Versuch zur Vorlesung: | |
| Elektrischer Schwingkreis (Versuchskarte Em056) | |
_______________________________________________
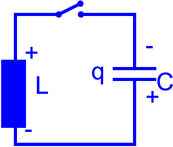
________________________________________________________________
Der Kondensator soll zur Zeit t = 0 auf die Spannung UC,0aufgeladen sein. Zur Zeit t = 0 wird der Schalter geschlossen. Die Differentialgleichung dieser Schaltung lautet:
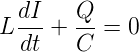 | (4.80) |
Wir differenzieren einmal und bekommen
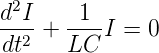 | (4.81) |
Dies ist die aus der Mechanik bekannte Schwingungsdifferentialgleichung. Durch Analogieschluss sieht man, dass die Resonanzfrequenz
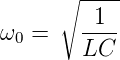 | (4.82) |
ist.
__________________________________________________________________________
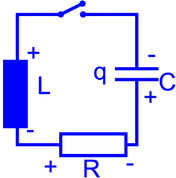
________________________________________________________________
Der gedämpfte Schwingkreis enthält neben dem Kondensator und der Spule auch einen Widerstand. Die Differentialgleichung des gedämpften Schwingkreises ist
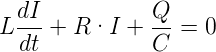 | (4.83) |
Wir differenzieren einmal und bekommen
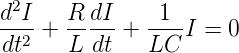 | (4.84) |
Analog zur Mechanik ist die 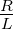 der Dämpfungsterm. Das in
der Mechanik berechnete Verhalten eines schwingungsfähigen
Systems gilt auch für den elektrischen Schwingkreis.
der Dämpfungsterm. Das in
der Mechanik berechnete Verhalten eines schwingungsfähigen
Systems gilt auch für den elektrischen Schwingkreis.
Wenn der elektrische Schwingkreis von einer Wechselspannungsquelle getrieben wird, ergeben sich die gleichen Phänomene wie bei einem getriebenen Pendel, also auch eine Resonanz.
Anwendungen
__________________________________________________________________________
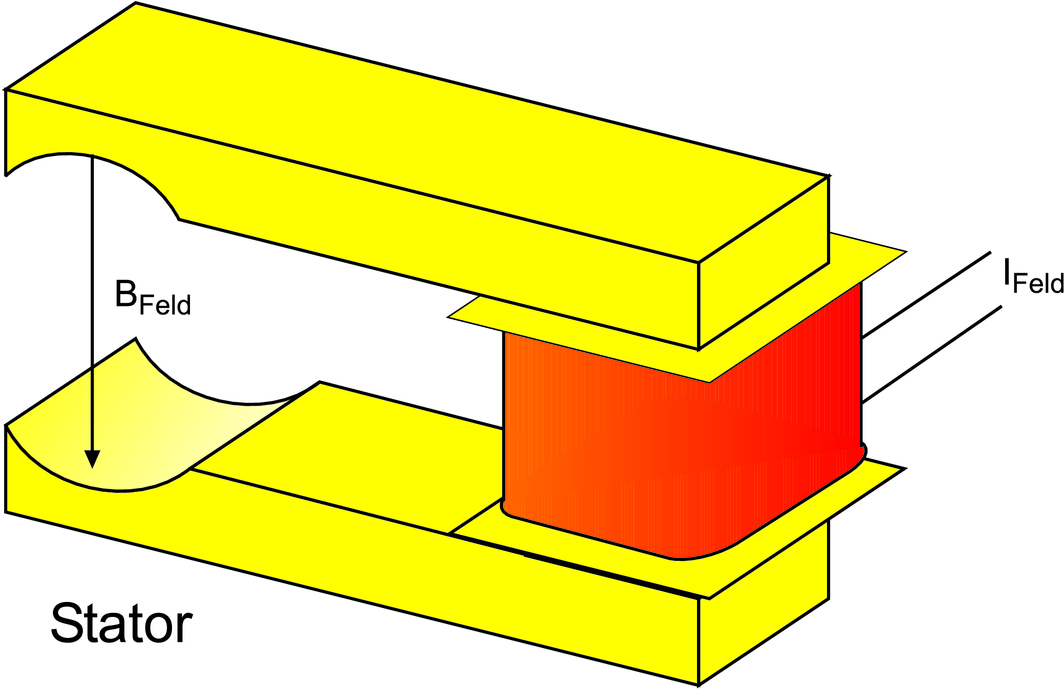
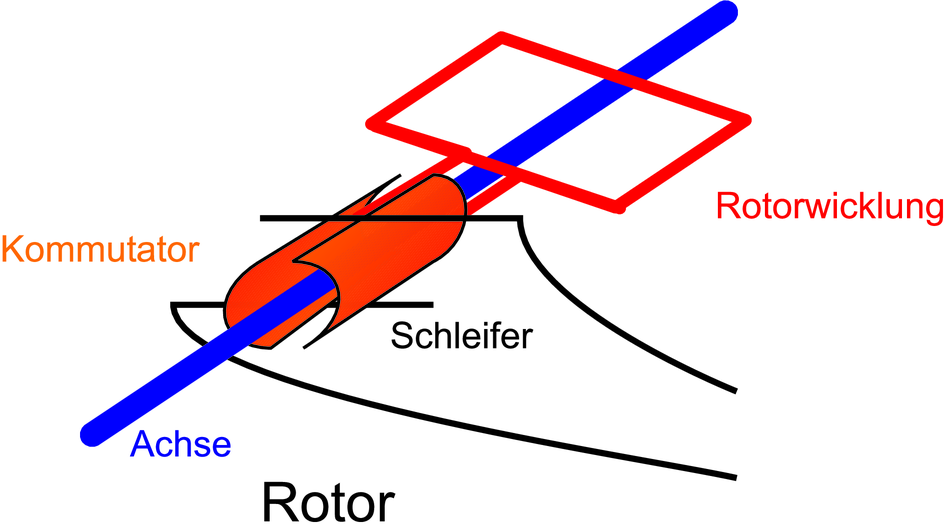
Bestandteile eines Elektromotors. Links der Stator, rechts der Rotor mit dem Kommutator.
_____________________________________________________________________
Ein Elektromotor besteht aus zwei teilen, dem Stator, der
das Magnetfeld  erzeugt und dem Rotor, der in diesem
Magnetfeld rotiert. Die Richtung des Stromflusses im Rotor
wird durch den Kommutator gesteuert.
erzeugt und dem Rotor, der in diesem
Magnetfeld rotiert. Die Richtung des Stromflusses im Rotor
wird durch den Kommutator gesteuert.
| Versuch zur Vorlesung: | |
| Elektromotor und -generator (Versuchskarte EM101) | |
_______________________________________________
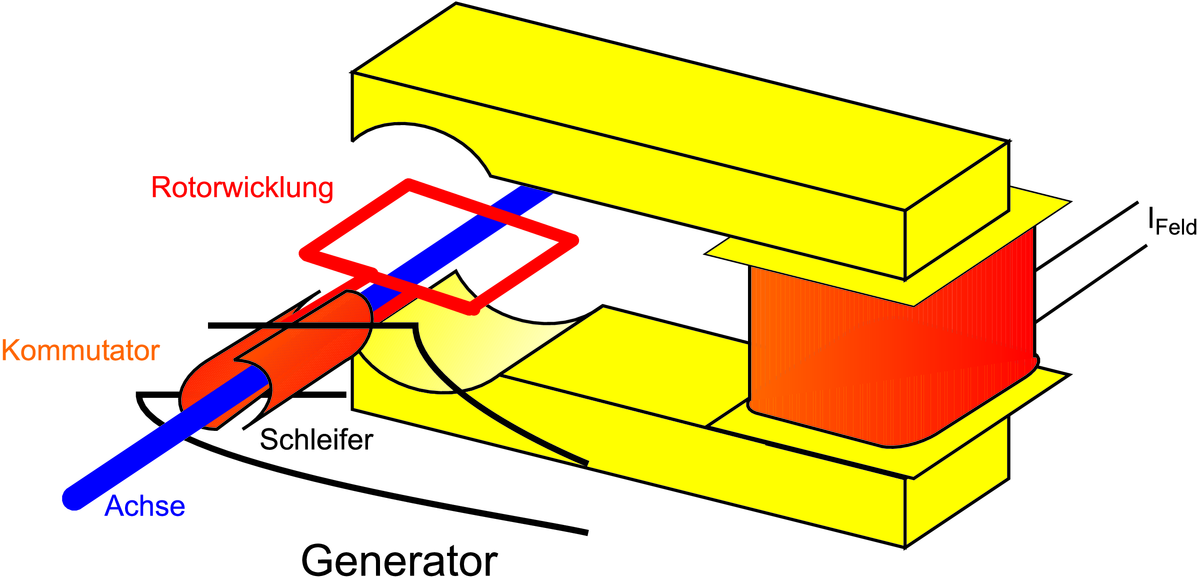
Dieses Bild zeigt einen aufgebauten Elektromotor.
_____________________________________________________________________
Wir betrachten zuerst den Elektromotor als Generator. Der Fluss durch die Leiterschlaufe mit N Windungen, einer Fläche A und einem Widerstand R ist
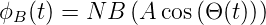 | (4.85) |
wobei Θ der Winkel zwischen der Normalen der Fläche der Leiterschlaufe und der Richtung des Magnetfeldes ist. Mit Θ = ωt + δ wird der zeitabhängige Fluss durch eine sich mit ω drehende Leiterschlaufe
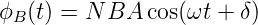 | (4.86) |
Durch Ableiten erhält man die Induktionsspannung
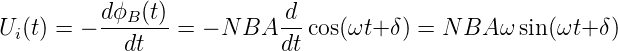 | (4.87) |
Die induzierte effektive Spannung ist
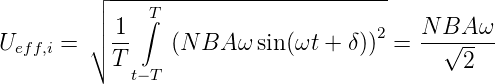 | (4.88) |
Wenn die Leiterschlaufe mit N Windungen mit Spannung versorgt wird, arbeitet sie als Motor. Die Leiterschlaufe habe, wie oben erwähnt, den Widerstand R. Die angelegte Spannung sei U0 und konstant. Für die folgende Rechnung setzen wir δ = 0.
Durch den Strom I(t) wird nach Gleichung (3.24) mit dem magnetischen Moment m = NAI ein Drehmoment
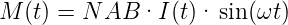 | (4.89) |
erzeugt.1 .
Während in Gleichung (4.85) der Winkel Θ(t) der Winkel
zwischen der Flächennormale und der Richtung der
magnetischen Induktion 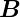 ist, ist hier der gleiche Winkel
der Winkel zwischen dem magnetischen Moment der
Leiterschleife
ist, ist hier der gleiche Winkel
der Winkel zwischen dem magnetischen Moment der
Leiterschleife 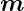 (t) und der magnetischen Induktion
(t) und der magnetischen Induktion 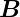 . Das
Drehmoment ist nach Gleichung (3.25) durch
. Das
Drehmoment ist nach Gleichung (3.25) durch 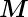 =
= 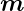 ×
×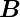 gegeben. Das momentane magnetische Moment hängt vom
momentanen Strom ab, und damit auch das momentane
Drehmoment. Beide hängen damit von der wirkenden
Spannung Ur(t) = U0 − Ui(t) ab
gegeben. Das momentane magnetische Moment hängt vom
momentanen Strom ab, und damit auch das momentane
Drehmoment. Beide hängen damit von der wirkenden
Spannung Ur(t) = U0 − Ui(t) ab
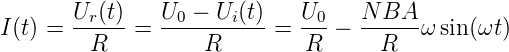 | (4.90) |
Unser Motor hat einen Kommutator, der nach einer halben Umdrehung das Vorzeichen der angelegten Spannung invertiert. Wir müssen also mit den Strömen
rechnen. Das Drehmoment wird dann
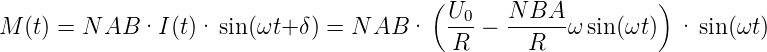 | (4.92) |
Dabei muss für I(t) die beiden Teilströme eingeteilt werden. Das Drehmoment als Funktion der Zeit ist dann
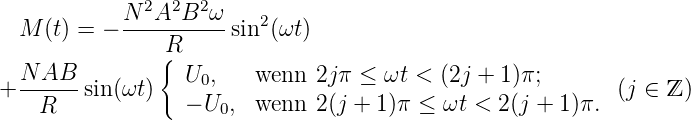 | (4.93) |
Das mittlere Drehmoment bei einem Motor, bei dem der Kommutator immer bei dem Winkel, bei dem das Drehmoment null wird, das Vorzeichen ändert, ist bei ω = 2π∕T
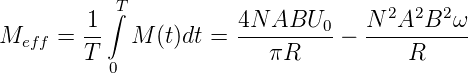 | (4.94) |
Im Mittel ist das Drehmoment des ruhenden Motors
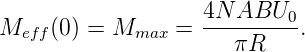 | (4.95) |
Die maximale Drehzahl ist (wenn Meff(ωmax) = 0)
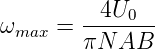 | (4.96) |
Diese Charakteristik (Nebenschlussmotor) hat man immer dann, wenn das erregende Feld B unabhängig von der Drehzahl ist, bei Permanentmagneten oder wenn die Spule für die Erregerwicklung parallel zum Anker angeschlossen ist. Will man die Drehzahl erhöhen, muss man das Feld B schwächen.
Gemittelte Betrachtung Die vorherige Betrachtung kann auch gemittelt durchgeführt werden.
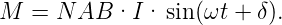 | (4.97) |
Das mittlere Drehmoment bei einem Motor, bei dem der Kommutator immer bei dem Winkel, bei dem das Drehmoment null wird, das Vorzeichen ändert, ist
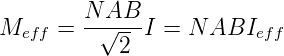 | (4.98) |
Mit dem Widerstand des Ankers R kann man den mittleren Strom aus der wirkenden Spannung U0 − Ueff,i berechnet werden
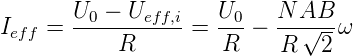 | (4.99) |
Die angelegte Spannung U0 ist eine Gleichspannung, deshalb darf kein Effektivwert berechnet werden. Damit hängt das Drehmoment von der Drehzahl ab
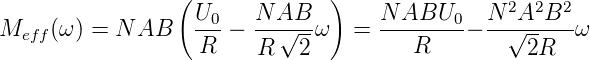 | (4.100) |
Das Drehmoment des ruhenden Motors ist also
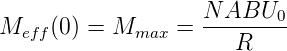 | (4.101) |
und die maximale Drehzahl (mit Meff(ωmax) = 0) ist
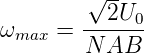 | (4.102) |
Verglichen mit Gleichung (4.96) hat sich nur der Vorfaktor
geändert, von 4∕π ≈ 1.273 zu 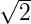 ≈ 1.414. Mit der
gemittelten Betrachtung überschätzen wir die maximale
Drehzahl!
≈ 1.414. Mit der
gemittelten Betrachtung überschätzen wir die maximale
Drehzahl!
__________________________________________________________________________
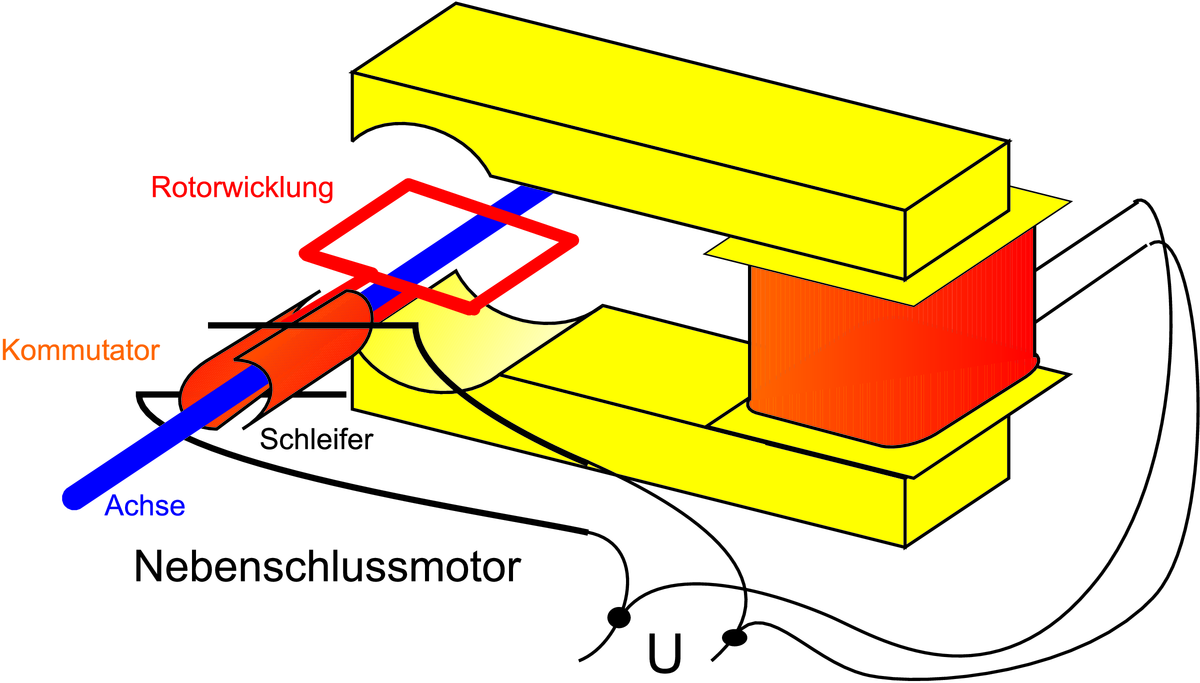
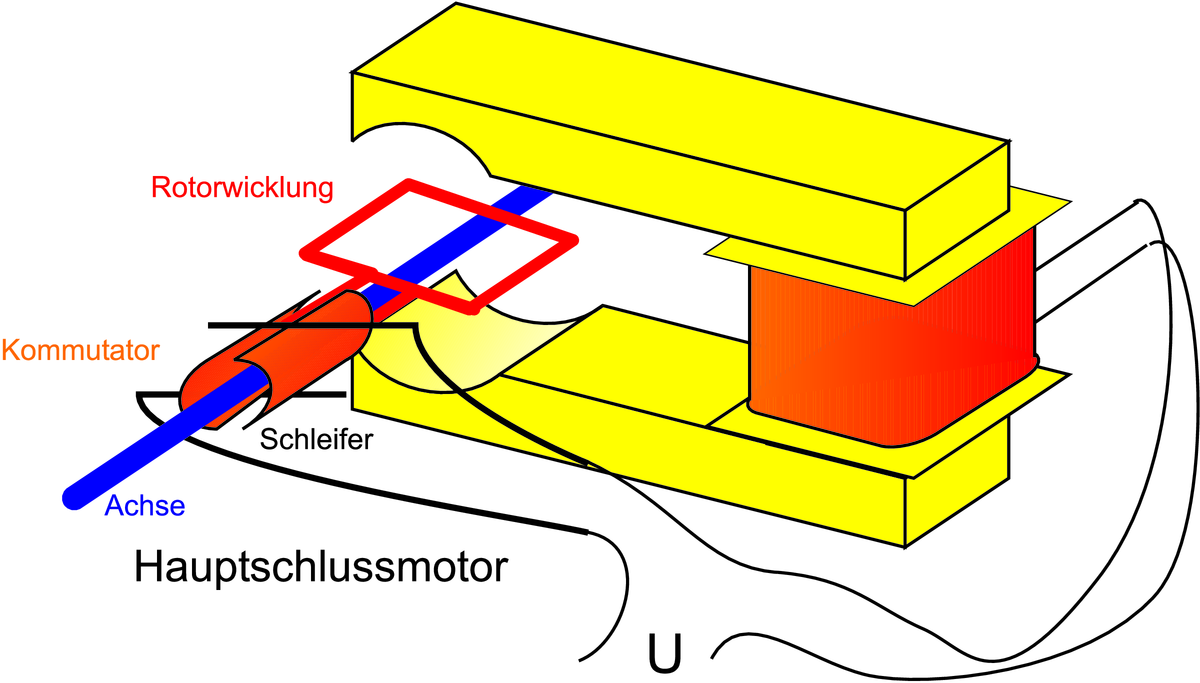
Links ist die Schaltung des Nebenschlussmotors, rechts die des Hauptschlussmotors gezeigt.
_____________________________________________________________________
Ist wie beim Hauptschlussmotor die Erregerwicklung in Serie zur Ankerwicklung geschaltet, gibt es keine maximale Drehzahl. Eine lange Zylinderspule (Länge ℓ, Windungszahl N) hat das Magnetfeld
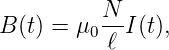 | (4.103) |
sofern der Einfluss der Induktivität vernachlässigt werden kann. Diese würde für eine Änderung der Amplitude und der Phase sorgen. Für andere Geometrien gilt das gleiche Gesetz, aber mit einem geometrieabhängigen Vorfaktor K′.
Im statischen Falle ist der Strom nur vom
Gleichstromwiderstand RE der Erregerspule abhängig. Sonst
müsste 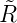 = RE + ZLE verwendet werden.
= RE + ZLE verwendet werden.
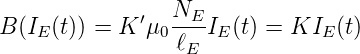 | (4.104) |
wobei alle Vorfaktoren in den Faktor K zusammengezogen wurden. Spannung und Strom an der Feldspule oder Erregerspule hängen über
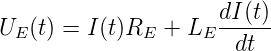 | (4.105) |
zusammen.
Der durch den Anker fliessende Strom ist mit
Ui(t) = −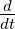
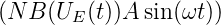 und I(t) = IE(t) sowie
dem Resultat von Gleichung (4.105) gegeben.
und I(t) = IE(t) sowie
dem Resultat von Gleichung (4.105) gegeben.
![I(t) = U0-−-UE-(t) −-Ui(t)
R [ ]
U0- RE-- LE-dI-(t) -1 d-
= R − I(t) R − R dt − R − dt (N B (I(t))A sin(ωt ))
E](el-2017958x.png) | (4.106) |
Eingesetzt
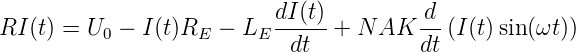 | (4.107) |
und umgestellt
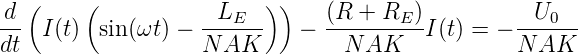 | (4.108) |
Wenn der Kommutator den Stromfluss im Anker umstellt, bekommt man
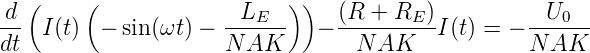 | (4.109) |
Die Lösungen dieser beiden Differentialgleichungen müssen beim Umschalten des Kommutators jeweils gleich sein. I(t) kommt nur linear vor, das heisst, man kann die Gleichungen als komplexe Gleichungen schreiben, indem sin(ωt) → i exp(iωt) gesetzt wird. Weiter kann
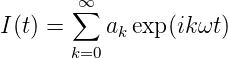 | (4.110) |
gesetzt werden. Dies führt zu einer Rekursion für die Koeffizienten ak. Noch unbekannt ist der Phasenwinkel zwischen den beiden
Die weitere Rechnung ist kompliziert. Man müsste auch die Induktivität der Spulen berücksichtigen.
Gemittelte Betrachtung
Der durch den Anker fliessende Strom ist mit
Ueff,i = NB(UE)Aω∕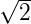 durch
durch
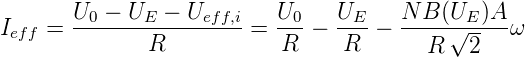 | (4.111) |
gegeben.
Da Ieff = IE,eff und UE = RE·IE,eff sind, gilt
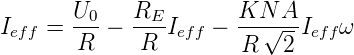 | (4.112) |
oder
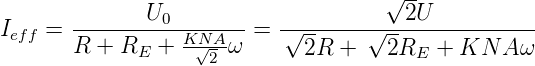 | (4.113) |
Damit wird das Drehmoment
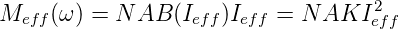 | (4.114) |
Eingesetzt bekommt man
![2N AKU 20
Meff (ω ) = [√-------√---------------]2-
2R + 2RE + KN A ω](el-2017968x.png) | (4.115) |
Meff(ω) ist für alle ω grösser als null. Dieser Motor hätte, ohne Lagerreibung, eine unendlich grosse maximale Drehzahl. Das Startdrehmoment für ω = 0 ist
![N-AKU---2-
Meff (0) = Mmax = [R + R ]2
E](el-2017969x.png) | (4.116) |
__________________________________________________________________________
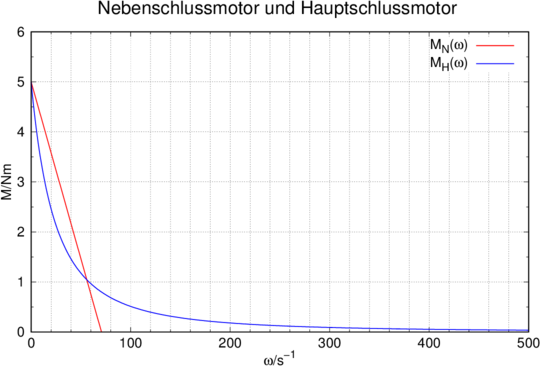
Kennlinien von Nebenschluss- und Hauptschlussmotoren aus der gemittelten Betrachtung. Die Kurven wurden mit N = 1000, A = 0.001 m2, U = 5 V, R = 0.1 Ω und B = 0.1 T. Die beiden Motoren sind so berechnet, dass sie das gleiche Startdrehmoment und dass RE = R∕2 ist (eine vernünftige Annahme).
_____________________________________________________________________
| Versuch zur Vorlesung: | |
| Linearmotor (Versuchskarte EM113) | |
| Versuch zur Vorlesung: | |
| Betatron (Versuchskarte EM167) | |
Die Idee hinter der Konstruktion des Betatrons ist, dass bei
einem zeitabhängigen 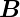 -Feld nach rot
-Feld nach rot 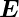 = −∂
= −∂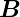 ∕∂t auch
ein zeitabhängiges
∕∂t auch
ein zeitabhängiges 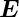 -Feld existiert.
-Feld existiert.
__________________________________________________________________________

Skizze eines Betatrons
_____________________________________________________________________
Nach dem Induktionsgesetz rot 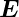 = −∂
= −∂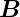 ∕∂t hat das
durch ein in die z-Richtung zeigende Magnetfeld induzierte
elektrische Feld keine z-Komponente. Nehmen wir an, dass
das
∕∂t hat das
durch ein in die z-Richtung zeigende Magnetfeld induzierte
elektrische Feld keine z-Komponente. Nehmen wir an, dass
das 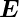 -Feld eine Radialkomponente hätte. Sie könnte zum
Beispiel in die y-Richtung zeigen. Rotieren wir die ganze
Anordnung um π um die y-Achse und kehren die Richtung
des
-Feld eine Radialkomponente hätte. Sie könnte zum
Beispiel in die y-Richtung zeigen. Rotieren wir die ganze
Anordnung um π um die y-Achse und kehren die Richtung
des 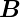 -Feldes um, haben wir wieder die Ausgangsanordnung.
Mit der Richtungsumkehr von
-Feldes um, haben wir wieder die Ausgangsanordnung.
Mit der Richtungsumkehr von 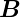 hat aber auch
hat aber auch 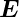 die
Richtung geändert (Induktionsgesetz). Dies ist aber im
Widerspruch zur Ausgangssituation. Deshalb kann es kein
radiales
die
Richtung geändert (Induktionsgesetz). Dies ist aber im
Widerspruch zur Ausgangssituation. Deshalb kann es kein
radiales 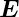 -Feld geben: das
-Feld geben: das 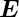 -Feld ist tangential und
beschleunigt die geladenen Teilchen. Damit die Teilchen auf
der Kreisbahn bleiben, muss
-Feld ist tangential und
beschleunigt die geladenen Teilchen. Damit die Teilchen auf
der Kreisbahn bleiben, muss
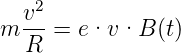 | (4.117) |
oder
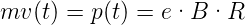 | (4.118) |
Das zweite Newtonsche Axiom in tangentialer Richtung angewandt bedeutet
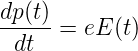 | (4.119) |
Mit der Integralform des Induktionsgesetzes erhält man mit einer stationären Kreisbahn S(R) mit dem Radius R
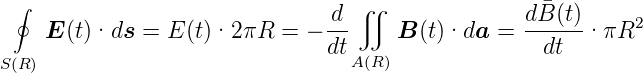 | (4.120) |
wobei das über die Fläche des Kreises gemittelte 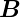 -Feld
ist. Durch Kombination der obigen Gleichungen und unter
Berücksichtigung der Vorzeichen erhalten wir
-Feld
ist. Durch Kombination der obigen Gleichungen und unter
Berücksichtigung der Vorzeichen erhalten wir
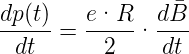 | (4.121) |
Die Integration mit den Anfangsbedingungen p(0) = 0 und B(0) = 0 liefert
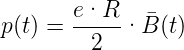 | (4.122) |
Der Vergleich mit der Bedingung für die Zentripetalkraft liefert die Wideroe-Bedingung
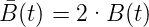 | (4.123) |
Diese Bedingung kann durch eine geeignete Wahl der Form der Polschuhe erreicht werden.
__________________________________________________________________________
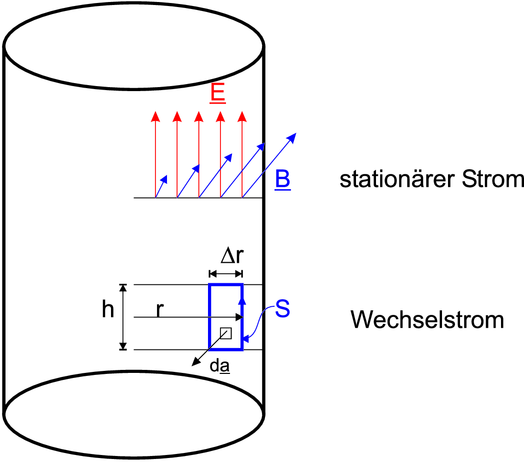
Berechnung des Skin-Effektes
_____________________________________________________________________
Bei Gleichstrom in einem zylindrischen Leiter ist das elektrische Feld konstant über dem Querschnitt. Nach dem Ampèreschen Durchflutungsgesetz (Siehe Gleichung (3.32)) ist das Magnetfeld proportional zum Abstand.
Für den Fall eines Wechselstroms mit niedriger Frequenz müssen wir das Induktionsgesetz berücksichtigen. Nach dem Induktionsgesetz gilt für die zeitunabhängige Kurve S, die auf einer Ebene, in der auch die Zylinderachse liegt, liegt
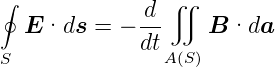 | (4.124) |
Für die eingezeichnete Schlaufe gilt (d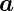 ist antiparallel zu
ist antiparallel zu
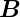 )
)
![d(− ¯B)
h [E (r) − E(r − Δr )] = ------· (− h ·Δr )
dt](el-2017993x.png) | (4.125) |
wobei wieder das über die Fläche Δr·h gemittelte Magnetfeld ist. Als Zwischenresultat bekommen wir:
![¯
[E-(r) −-E-(r-−-Δr-)]= d(B-)
Δr dt](el-2017994x.png)
Da der Strom zeitabhängig ist, muss auch das 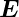 -Feld
ortsabhängig sein. Eine homogene Stromverteilung bei
Wechselstrom ist bei einem Ohmschen Leiter nicht vereinbar
mit dem Induktionsgesetz. Die Taylorentwicklung von
Gleichung (4.124) liefert die betragsmässige Bedingung
-Feld
ortsabhängig sein. Eine homogene Stromverteilung bei
Wechselstrom ist bei einem Ohmschen Leiter nicht vereinbar
mit dem Induktionsgesetz. Die Taylorentwicklung von
Gleichung (4.124) liefert die betragsmässige Bedingung
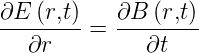 | (4.126) |
Das elektrische Feld muss also bei Wechselstrom mit zunehmendem Abstand vom Radius zunehmen. Da der Gesamtstrom gegeben ist, ist die Stromdichte an der Oberfläche konzentriert. Dies ist der Skineffekt.
Anwendung
Die Berechnung der Skintiefe kann nach Jackson [Jac75, pp. 334-338]2 aus dem Ampèreschen Gesetz Gleichung (3.32), dem Faraday’schen Gesetz Gleichung (4.24) und dem mikroskopischen Ohm’schen Gesetz (3.2) abgeleitet werden.
Wir beginnen mit den drei Gleichungen
Wir nehmen mit Jackson eine harmonische Welle an, also
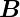 =
= 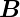 0 exp
0 exp 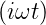 und
und 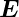 =
= 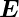 0 exp
0 exp 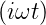 . Damit können die
obigen Gleichungen umgeschrieben werden
. Damit können die
obigen Gleichungen umgeschrieben werden
Wenn 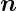 der nach aussen zeigende Normalenvektor auf die
Grenzfläche Vakuum-Metall ist und ξ die nach innen zeigende
Koordinate ist, kann in der Nähe der Oberfläche der
Nabla-Operator als
der nach aussen zeigende Normalenvektor auf die
Grenzfläche Vakuum-Metall ist und ξ die nach innen zeigende
Koordinate ist, kann in der Nähe der Oberfläche der
Nabla-Operator als
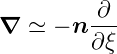 | (4.133) |
geschrieben werden. Gleichungen (4.131) und (4.132) lauten dann
Um die beiden Gleichungen zu kombinieren, multiplizieren
wir mit dem Kreuzprodukt oder Vektorprodukt von
links mit −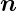
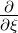 und verwenden weiter, dass nach (C.1)
und verwenden weiter, dass nach (C.1)
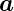 ×
×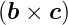 =
= 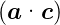
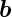 −
−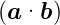
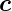 ist.
ist.
Diese Gleichung hat zwei Komponenten. Es gibt Summanden,
die in die Richtung von 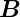 0 zeigen und Summanden, die in die
Richtung von
0 zeigen und Summanden, die in die
Richtung von 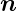 zeigen. Die Summanden für die beiden
Richgtungen ergeben die folgenden zwei Gleichungen, da das
Resultat ja unabhängig von den einzelnen Vektoren sein
muss.
zeigen. Die Summanden für die beiden
Richgtungen ergeben die folgenden zwei Gleichungen, da das
Resultat ja unabhängig von den einzelnen Vektoren sein
muss.
Gleichung (4.137) ist eine Differentialgleichung zweiter
Ordnung. Deshalb machen wir den Lösungsansatz
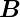 0(ξ) =
0(ξ) = 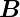 0,0 exp
0,0 exp 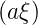 und setzen
und setzen
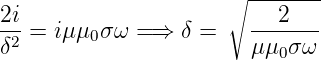 | (4.139) |
und erhalten über
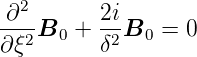 | (4.140) |
die charakteristische Gleichung
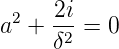 | (4.141) |
die Lösungen
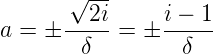 | (4.142) |
Das Vorzeichen + ist physikalisch sinnvoll (es gibt keine zunehmende Amplitude). Damit ist besteht die Lösung aus einem exponentiellen Abfall mit der Abfalllänge δ und einem örtlich oszillierenden Teil, also
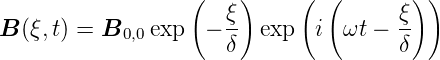 | (4.143) |
Damit ist
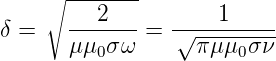 | (4.144) |
die Skintiefe bei der Frequenz ω eines Metalls mit der relativen Permeabilität μ und der Leitfähigkeit σ. Aus Gleichung (4.144) kann abgelesen werden, dass
___________________________________________________________________________
| 1 Hz | 16.67 Hz | 50 Hz | 100 Hz | 1 kHz | 10 kHz | 100 kHz | 1 MHz | |
| Kupfer | 66 m m | 16 m m | 9.3 m m | 6.6 m m | 2.1 m m | 660 μ m | 21 μ m | 66 μ m |
| Aluminium | 83 mm | 20 mm | 12 mm | 8.3 mm | 2.6 mm | 830 μm | 26 μm | 83 μm |
| Eisen (μ = 104) | 1.6 mm | 390 μm | 230 μm | 160 μm | 50 μm | 16 μm | 5.0 μm | 1.6 μm |
| Edelstahl (μ = 300) | 25 mm | 6.0 mm | 3.5 mm | 2.5 mm | 780 μm | 250 μm | 78 μm | 25 μm |
| Meerwasser | 230 m | 55 m | 32 m | 23 m | 7.1 m | 2.3 m | 710 mm | 23 mm |
| Leitungswasser | 7.1 k m | 1.7 k m | 1.0 k m | 712 m | 230 m | 71 m | 23 m | 7.1 m |
_______________________________________________________________________________________________
 Lizenzinformationen
Lizenzinformationen