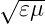6.6  Lichtgeschwindigkeit im Medium und Intensität

In einem Medium bewegen sich elektromagnetische Wellen langsamer. Die einfallende Welle regt die polarisierbaren Atome zum Schwingen an. Diese schwingen mit der gleichen Frequenz, aber mit einer frequenzabhängigen Phasenverschiebung. Die Resonanzfrequenz des Elektron-Atomrumpfsystems liegt im Ultravioletten. In der Summe wird die elektromagnetische Welle durch diese mit der zunehmenden Frequenz zunehmenden Phasenverschiebung verlangsamt. Mit dem (frequenzabhängigen) Brechungsindex n = 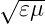bekommt man

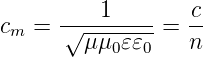(6.1)

wobei c die Lichtgeschwindigkeit im Vakuum ist. Die Brechzahl oder der Brechungsindex n gibt an, um wieviel langsamer elektromagnetische Wellen in einem Medium sind als im Vakuum. Die Intensität ist gegeben durch den Mittelwert des Poynting-Vektors 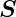(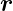) = 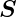₀(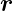) sin ²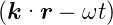. Für harmonische Schwingungen erhält man für die auf die Fläche mit der Flächennormale 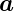einfallende Intensität

wenn E das elektrische Feld, d.h. eine der beiden möglichen Amplituden der elektromagnetischen Welle ist. 𝜀₀ = 8.8542·10⁻¹²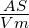 ist die Vakuumpermittivität und c = 2.9979·10⁸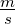 die Lichtgeschwindigkeit im Vakuum. Der Vorfaktor 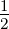entsteht durch die Mittelung über viele Perioden. Bei nichtmagnetischen Materialien (μ = 1) kann man auch schreiben:

Gleichung (6.2) kann auch so geschrieben werden:

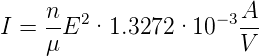(6.4)