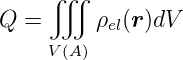
Nach der Gleichung (2.4) kann die gesamte Ladung in einem Raumgebiet begrenzt durch die Fläche A durch
|
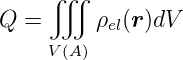| (2.1) |
ausgedrückt werden.
__________________________________________________________________________
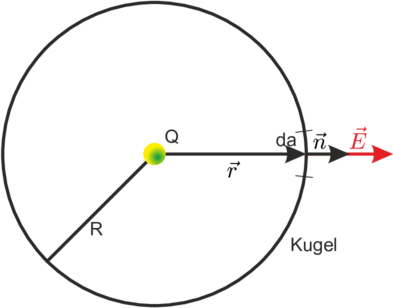
Integration über eine Kugelfläche mit einer Punktladung im Zentrum
_____________________________________________________________________
Wir betrachten eine kugelsymmetrische Situation um eine
Punktladung Q. Wir definieren den Normalenvektor am Ort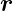 
als 
= 
∕
= 
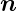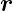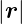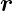∕r. Das Oberflächenelement da ist
da = r2 sin ΘdΘdφ.
Das elektrische Feld an der Kugeloberfläche ist
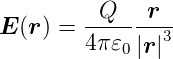 | (2.2) |
Wir erhalten damit das Gausssche Gesetz
Die Grösse Φ = ∫
Oberfläche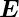
·d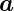
ist der Fluss des
Vektorfeldes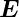 
oder der Fluss des elektrischen
Feldes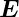 
durch die Oberfläche. Dieses Integral kann
vereinfacht werden, indem wir die dielektrische
Verschiebung
|
einführen. Die Einheit der dielektrischen Verschiebung ist
[
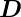] = C/m2 = As/m2.
Weiter ist
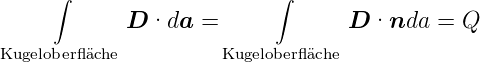 | (2.5) |
Allgemein gilt die obige Gleichung für beliebige geschlossene Flächen S, die das Volumen V (S) einschliesst.
__________________________________________________________________________
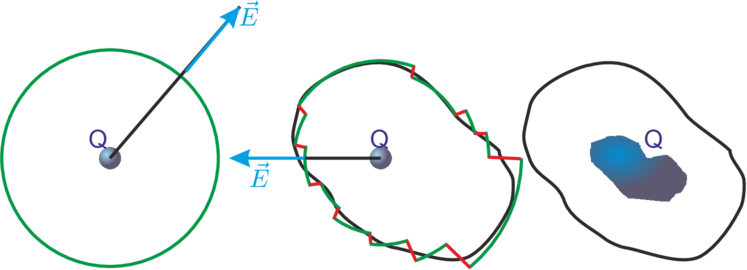
Approximation von beliebigen Oberflächen durch Kugelsegmente. Approximation einer kontinuierlichen Ladungsverteilung durch Punktladungen.
_____________________________________________________________________
Mit dem Gaussschen Satz (Gleichung (C.1)) kann die Gleichung umgeschrieben werden in
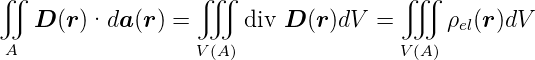 | (2.7) |
Diese Gleichung muss für alle Oberflächen S gelten. Deshalb müssen die Integranden gleich sein
|
Dies ist die Differentialform der Gleichung für die elektrische Verschiebung. Die physikalische Interpretation ist: die Ladungen sind die Quellen (Divergenz) der elektrischen Verschiebung und damit des elektrischen Feldes.
Im ladungsfreien Raum lautet Gleichung (2.8):
div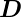 
(
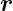) = 0. Diese Gleichung ist mathematisch äquivalent
zur Kontinuitätsgleichung strömender inkompressibler
Flüssigkeiten. Für deren Geschwindigkeitsfeld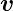 
(
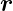) gilt
nämlich div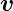 
(
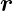) = 0.
Es gibt Moleküle, bei denen die negativen und die positiven
Ladungen getrennte Schwerpunkte haben. Eine negative
Ladung −q im Abstand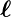 
von einer positiven Ladung q
heisst Dipol mit dem Dipolmoment
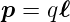 | (2.9) |
Die Einheit des Dipolmoments ist [p] = Cm. Der Vektor des Dipols zeigt von −q nach +q.
________________________________________________________________
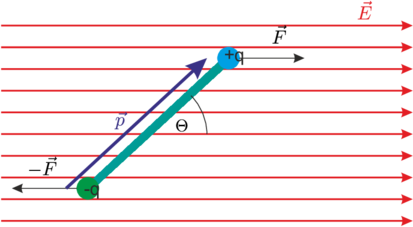
Kräfte auf einen Dipol im homogenen elektrischen Feld.
_____________________________________________________________________
Im homogenen elektrostatischen Feld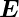 
wirkt auf die
positive Ladung die Kraft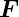 
und auf die negative Ladung
−
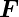. Zusammen bilden diese beiden Kräfte ein Kräftepaar
und erzeugen damit ein Drehmoment
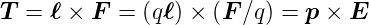 | (2.10) |
| Versuch zur Vorlesung: | |
| Drehmoment auf einen elektrischen Dipol (Versuchskarte ES-30) | |
| Folien zur Vorlesung vom 27. 04. 2009: PDF | |
Lizenzinformationen
