__________________________________________________________________________
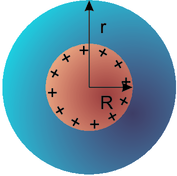
Berechnung eines Feldes einer Kugelschale
_____________________________________________________________________

(Siehe Tipler, Physik [TM04, pp. 645])
| Versuch zur Vorlesung: | |
| Elektrische Feldlinien (Versuchskarte ES-4) | |
Die elektrischen Felder
werden im Anhang berechnet.
| Versuch zur Vorlesung: | |
| Faraday-Becher (Versuchskarte ES-9) | |
| Versuch zur Vorlesung: | |
| Faraday-Käfig (Versuchskarte ES-21) | |
| Versuch zur Vorlesung: | |
| Van-de-Graaff-Generator (Versuchskarte ES-19) | |
Wir berechnen das elektrische Feld innerhalb und ausserhalb einer Kugelschale.
__________________________________________________________________________

Berechnung eines Feldes einer Kugelschale
_____________________________________________________________________
Die eingeschlossene Ladung durch die Kugelfläche mit dem Radius r > R ist
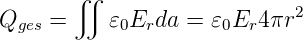 | (2.1) |
Da die Gesamtladung innerhalb dieser Fläche Q ist, haben wir
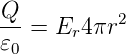 | (2.2) |
Damit ist für r > R
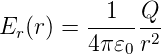 | (2.3) |
Das elektrische Feld einer homogen geladenen Kugelschale ist also ununterscheidbar vom elektrischen Feld einer Punktladung. Für r < R ist die eingeschlossene Ladung Q = 0. Damit ist auch Φges = Er4πr2 = 0 und folglich für r < R
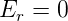 | (2.4) |
__________________________________________________________________________
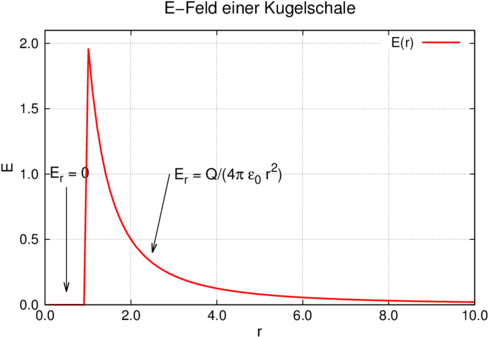
Die Feldverteilung einer homogen geladenen Kugelschale.
_____________________________________________________________________
Das elektrische Feld einer homogen geladenen Kugel mit dem Radius R wird analog berechnet. Ausserhalb der Kugel für r > R ist wie oben Φges = Er4πr2 = Q∕𝜀 0. Also ist für r > R
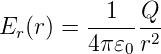 | (2.5) |
Wenn die Ladungsdichte ρel = Q∕V = Q∕(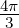 R3)
ist, ist die von einer zur homogen geladenen Kugel
konzentrischen Kugelschale mit r < R umschlossene Ladung
Q′ = ρelV (r) = ρel
R3)
ist, ist die von einer zur homogen geladenen Kugel
konzentrischen Kugelschale mit r < R umschlossene Ladung
Q′ = ρelV (r) = ρel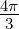 r3
r3
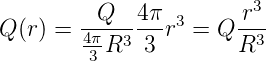 | (2.6) |
Weiter haben wir Er4π𝜀0r2 = Q. Also ist für r < R
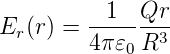 | (2.7) |
__________________________________________________________________________
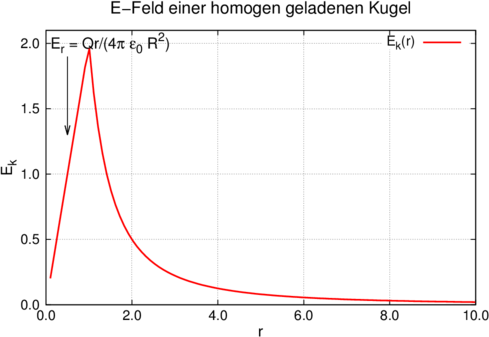
Elektrisches Feld einer homogen geladenen Kugel
_____________________________________________________________________
_____________________________________________________________________
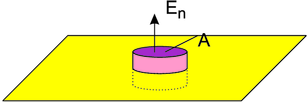
Integrationsfläche zur Berechnung des elektrischen Feldes einer Ebene
_____________________________________________________________________
Das elektrische Feld einer homogen geladenen Platte kann wie folgt berechnet werden.
Wenn σ die Ladungsdichte auf der Platte ist, dann ist
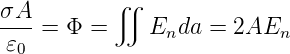 | (2.8) |
da sowohl die Unterseite wie auch die Oberseite einen Beitrag liefern.
Also ist
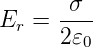 | (2.9) |
homogen im Raum.
__________________________________________________________________________
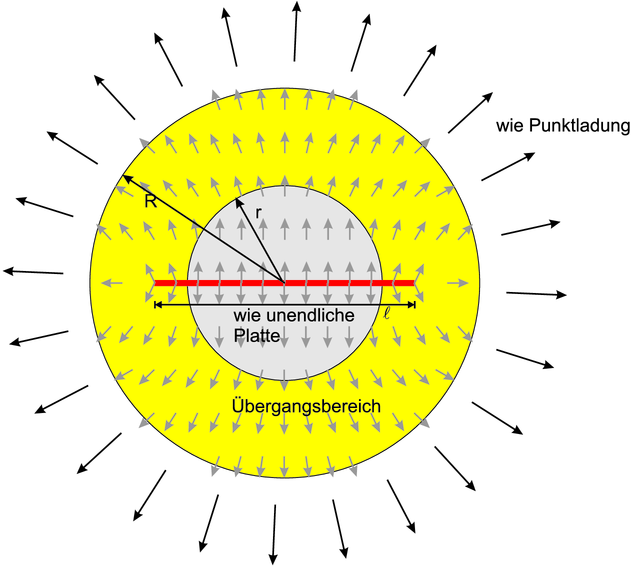
Elektrisches Feld um eine endliche Platte.
_____________________________________________________________________
Wir betrachten eine endliche ebene leitfähige Platte mit der Ausdehnung ℓ. Wir können drei Fälle unterscheiden:
Ein Beispiel für diese Art Flächenladungen sind
Klebestreifen. Andreas Döring [Dör01] gibt an,
dass Haftklebematerialien spezifische Haftenergien von
Et = 30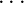 300 J/m2 haben. Die Definition von E
t ist
300 J/m2 haben. Die Definition von E
t ist
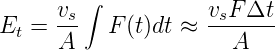
wobei vs = 0.01 m/s die Geschwindigkeit ist, mit der der Klebestreifen abgezogen wird und A die Kontaktfläche ist. Δt = 0.1 s ist die Loslösezeit. Die Haftkraft rührt von Ladungen her. Bei einer Flächenladungsdichte σ ist E = σ∕𝜀0. Die Kraft auf eine Flächenladungsdichte σ ist dann F∕A = σ2∕𝜀 0. Mit den Daten von Herrn Döring erhalten wir
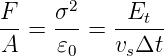
und daraus die Flächenladungsdichte
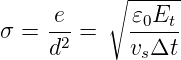
Dabei haben wir angenommen, dass Elementarladungen e im Abstand d angebracht sind. d ist dann
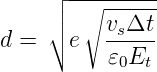
Wenn wir Et einsetzen erhalten wir d ≈ 10 nm…18 nm. Dieser Abstand korreliert gut mit den bekannten Moleküldurchmessern.
Bei zwei homogen geladenen Platten, deren Flächenladungsdichte vom Betrage her gleich sind, aber unterschiedliches Vorzeichen haben, heben sich die Felder ausserhalb der Platten auf. Gleichzeitig verstärken sich die Felder im Inneren: Die elektrische Feldstärke wird E = σ∕𝜀0.
__________________________________________________________________________
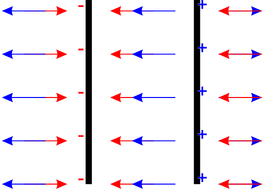
Elektrisches Feld entgegengesetzt gleich geladener Platten.
_____________________________________________________________________
Sind die Platten jedoch gleich geladen (oder ist die Oberflächenladung der Platten gleich), kompensieren sich die elektrischen Felder im Innern der Platte, verstärken sich aber im Aussenraum. Wieder ist im Aussenraum E = σ∕𝜀0.
__________________________________________________________________________
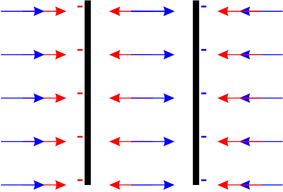
Elektrisches Feld gleich geladener Platten
_____________________________________________________________________
| Leiter haben in ihrem Inneren keine statischen elektrischen Felder. |
Da Ladungen im Inneren eines Leiters beweglich sind, folgt, dass das elektrische Feld an einer beliebigen Oberfläche, die sich ganz im Inneren eines Leiters befindet, null ist. Damit ist die umschlossene Ladung ebenso null. Daraus folgt, dass Ladungen sich nur an der Oberfläche eines Leiters befinden können.
Das elektrische Feld an der Oberfläche eines Leiters kann mit dem Gaussschen Gesetz berechnet werden. Wir betrachten eine zylinderförmige Fläche, deren eine Kreisfläche unter der Oberfläche des Leiters und deren andere über der Oberfläche des Leiters ist.
__________________________________________________________________________
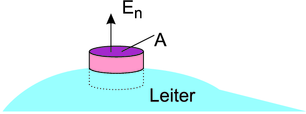
Integrationsfläche
_____________________________________________________________________
Der gesamte Fluss ist
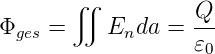 | (2.10) |
da das elektrische Feld im Inneren des Leiters null ist und die Höhe der Seitenflächen verschwinden soll, haben wir
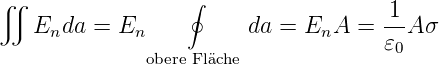 | (2.11) |
und
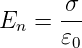 | (2.12) |
Aus dem Gaussschen Gesetz werden die zwei folgenden Schlüsse gezogen:
__________________________________________________________________________
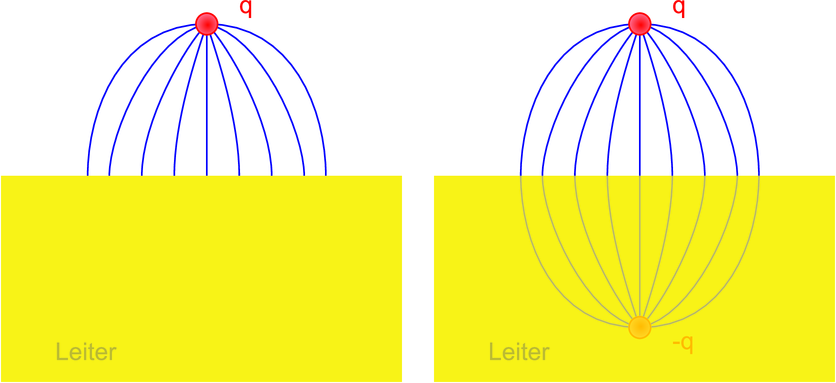
Links: Feldlinien in der Nähe eines Leiters. Rechts: Diese Feldlinien können mit einer Bildladung erklärt werden.
_____________________________________________________________________
Da elektrische Feldlinien immer senkrecht auf der Oberfläche
eines Leiters stehen müssen, sieht das Feldlinienbild einer
Punktladung in der Nähe eines Leiters wie die Hälfte
des Feldlinienbildes eines Dipols aus. Das elektrische
Feld der Punktladung erzeugt an der Oberfläche die
Influenzladung σ(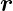 ), die das äussere Feld im Leiter
abschirmt. Formal kann das Feldlinienbild berechnet
werden, indem man zu einer Ladung q im Abstand a
von der Oberfläche eines Leiter im Leiter innen eine
Bildladung −q auch im Abstand a von der Oberfläche
verwendet.
), die das äussere Feld im Leiter
abschirmt. Formal kann das Feldlinienbild berechnet
werden, indem man zu einer Ladung q im Abstand a
von der Oberfläche eines Leiter im Leiter innen eine
Bildladung −q auch im Abstand a von der Oberfläche
verwendet.
Das Konzept der Bildladung zeigt, dass eine Ladung q im Abstand a von einem Leiter mit der Kraft
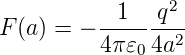 | (2.13) |
angezogen wird. Die Senkrechtkomponente (z-Komponente) des elektrischen Feldes ist im Abstand r vom Aufpunkt in der Leiteroberfläche
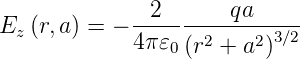 | (2.14) |
Damit ist die Oberflächenladungsdichte
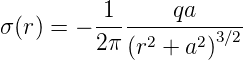 | (2.15) |
Mit analogen Überlegungen kann auch die Bildladungsdichte von kontinuierlichen Ladungsverteilungen berechnet werden5 .
 Lizenzinformationen
Lizenzinformationen