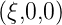 auf der x-Achse!
auf der x-Achse!

Entlang der x-Achse von x = 0 bis x = ℓ sei die Ladung Q
homogen verteilt. Zu berechnen ist das elektrische Feld für
einen Punkt P = 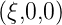 auf der x-Achse!
auf der x-Achse!
Die Linienladungsdichte ist
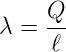
Das elektrische Feld bei P ist
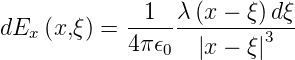
Wir integrieren über die Länge des Drahtes
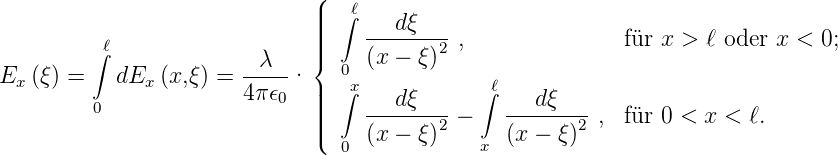
Die Lösung dieser Gleichung ist
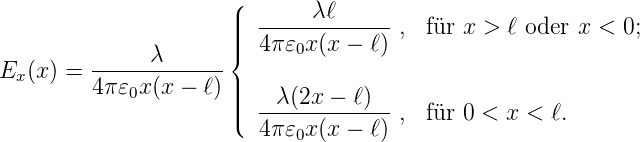
__________________________________________________________________________
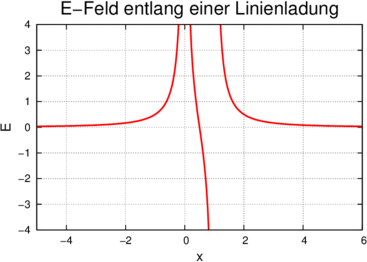
Elektrisches Feld entlang einer Linienladung.
_____________________________________________________________________
Wir berechnen nun das elektrische Feld entlang der
Mittelsenkrechten einer Linienladung der Länge ℓ. Zur
Berechnung legen wir das Koordinationssystem so, dass die
Ladungsverteilung von -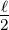 bis
bis 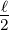 reicht. Aus Symmetriegründen
existiert auf der Mittelsenkrechten keine Komponente in
x-Richtung. Wir betrachten also die Komponente entlang y.
Am Punkt P =
reicht. Aus Symmetriegründen
existiert auf der Mittelsenkrechten keine Komponente in
x-Richtung. Wir betrachten also die Komponente entlang y.
Am Punkt P = 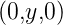 ist
ist
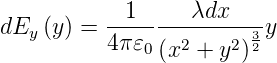
Ebenso ist
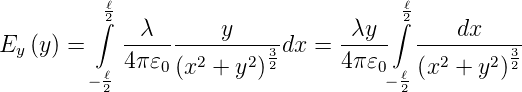
Nach Bronstein[BSMM08] ist
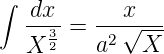
mit X = x2 + a2. Daraus folgt
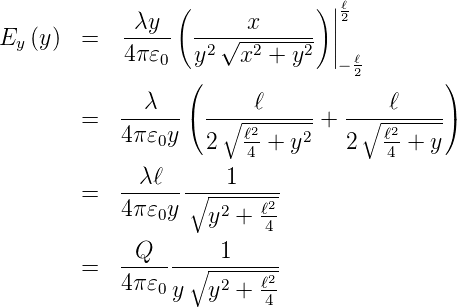
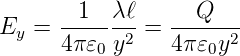
Für y «−ℓ bekommt man
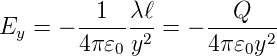
Wenn die Linienladung ”unendlich” ausgedehnt ist, gilt
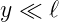
Dann ist
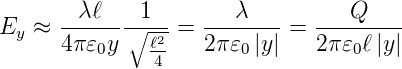
_________________________________________
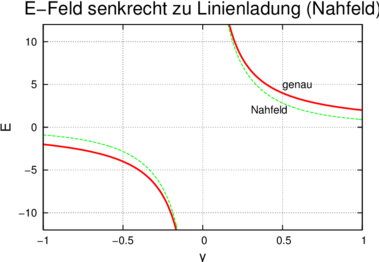
Elektrisches Feld senkrecht zu einer Linienladung.
_____________________________________________________________________
 Lizenzinformationen
Lizenzinformationen