 -Feld ist aus
Symmetriegründen radial symmetrisch. Der Fluss durch die
Fläche ist:
-Feld ist aus
Symmetriegründen radial symmetrisch. Der Fluss durch die
Fläche ist:

Der Zylindermantel habe den Radius R, die Flächenladungsdichte
sei σ. Wir betrachten eine Zylinderfläche koaxial zur
geladenen Fläche mit dem Radius r < R. Das  -Feld ist aus
Symmetriegründen radial symmetrisch. Der Fluss durch die
Fläche ist:
-Feld ist aus
Symmetriegründen radial symmetrisch. Der Fluss durch die
Fläche ist:

Da keine Ladung umschlossen wird, ist
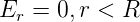
Für r > R gilt
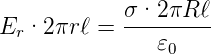
oder
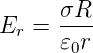
_______________________________________________________________
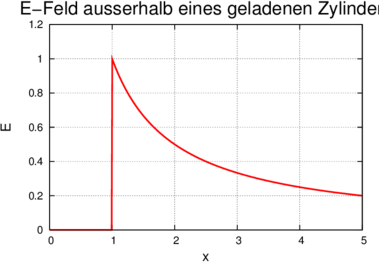
_____________________________________________________________________
 Lizenzinformationen
Lizenzinformationen