Up: PHYS1100 Grundkurs I Skript: PDF-Datei
Othmar Marti, (othmar.marti@uni-ulm.de)
Date: 20. 1. 2006 und 23. 1. 2006
|
|
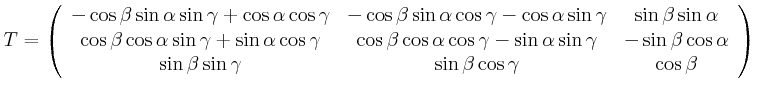
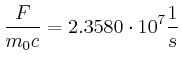
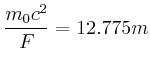
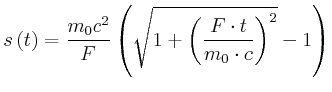
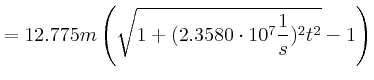 |
||
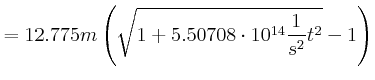 |
||
 |
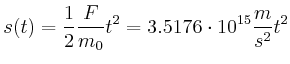
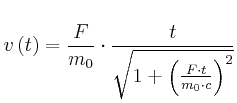
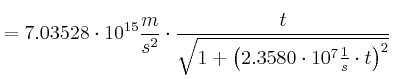 |
||
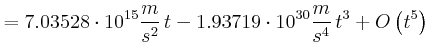 |
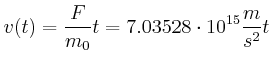
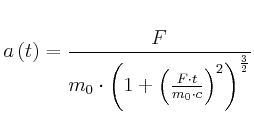
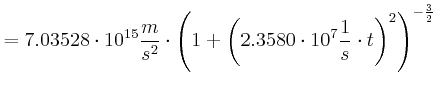 |
||
 |
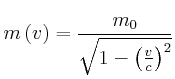
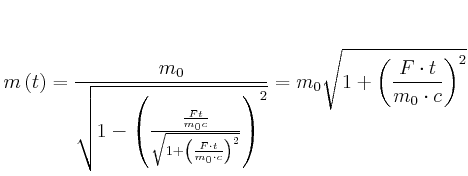
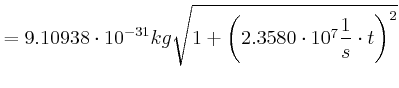 |
||
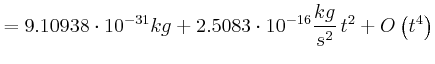 |
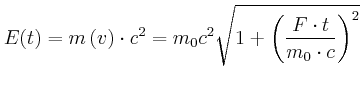
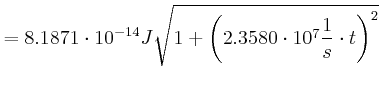 |
||
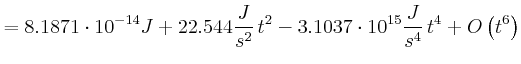 |
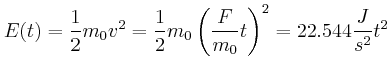
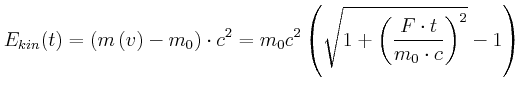
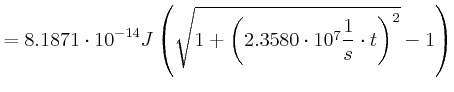 |
||
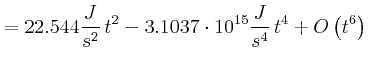 |
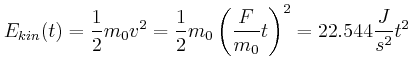
Es gilt:
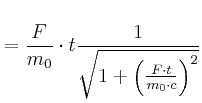 |
||
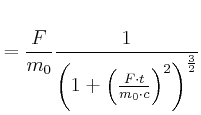 |
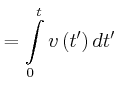 |
||
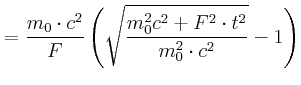 |
||
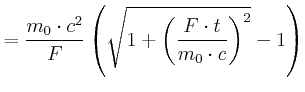 |
Beschleunigt wird auf der 1. Hälfte der Strecke:
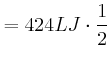 |
||
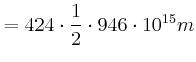 |
||
Auflösen nach ![]() :
:
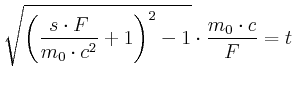
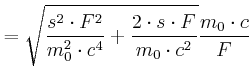 |
||
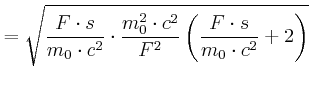 |
||
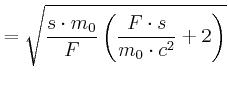 |
||
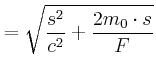 |
Die Reisedauer ist:
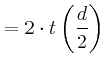 |
||
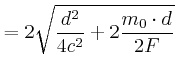 |
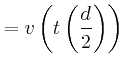 |
||
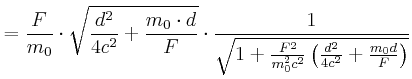 |
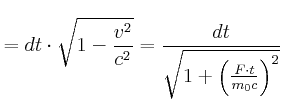 |
||
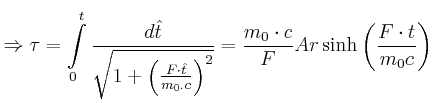 |
||
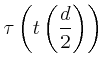 |
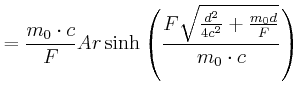 |
|
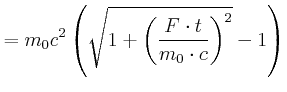 |
||
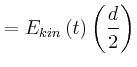 |
||
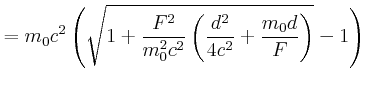 |
![]() aus Gewichtskraft:
aus Gewichtskraft:
![]()
![]() am Äquator:
am Äquator:
![]()
![]()
oder:
![]()
![]()
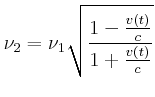
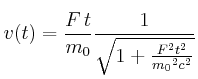
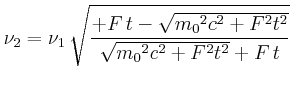
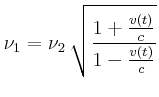
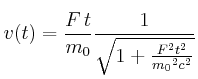
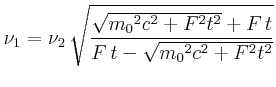
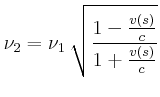
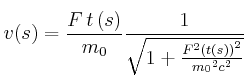
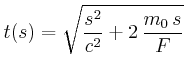
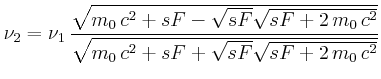
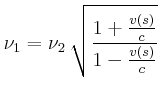
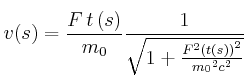
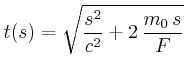
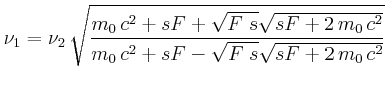
Geschwindigkeit:
![]() ,
, ![]()
Vollständig plastischer Stoss: gleiche Massen, gleiche Geschwindigkeiten, entgegengesetzt
Die Massen sind nach dem Stoss in Ruhe.
Dissipierte Energie:
![]()
Tatsächlich: Annihilation, d.h. Paarvernichtung; Elektron und Positron werden vernichtet, 2 Photonen gleicher Energie entstehen.
Dissipierte Energie:
![]()
z.B. ![]()
![]()
![]()
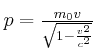
relativistischer Energiesatz:
![]()
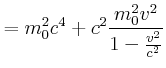 |
||
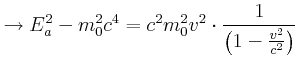 |
||
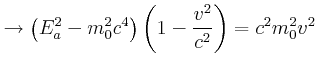 |
||
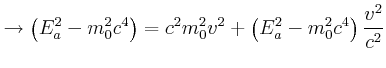 |
||
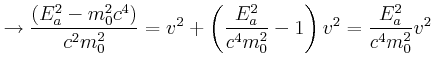 |
||
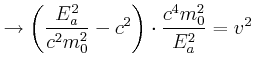 |
||
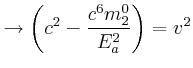 |
||
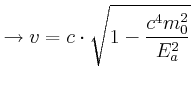 |
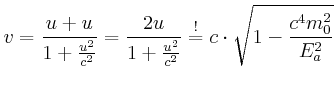
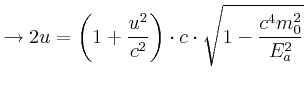
Wir müssen die quadratische Gleichung lösen:
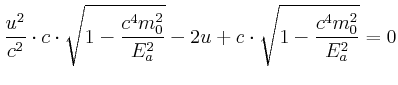
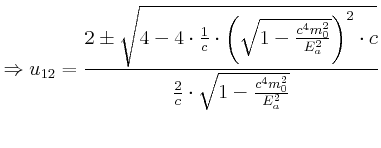 |
||
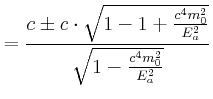 |
||
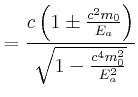 |
||
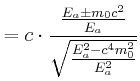 |
||
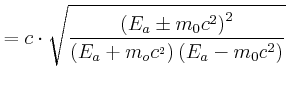 |
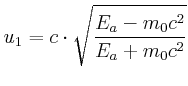
physikalisch sinnvoll, da ![]() grösser c wäre.
grösser c wäre.
Die Geschwindigkeit ![]() gibt an, wie schnell sich
gibt an, wie schnell sich ![]() auf den Schwerpunkt zubewegt. Das entspricht von
auf den Schwerpunkt zubewegt. Das entspricht von
![]() aus gesehen der Schwerpunktgeschwindigkeit.
aus gesehen der Schwerpunktgeschwindigkeit.
Eine alternative Berechnung läuft über die Lage des Schwerpunktes. Im Laborsystem sei ![]() die Position
der bewegten Masse
die Position
der bewegten Masse
![]() ,
, ![]() die Position der ruhenden Masse und
die Position der ruhenden Masse und
![]() die Lage des Schwerpunktes. Dann ist
die Lage des Schwerpunktes. Dann ist
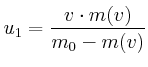
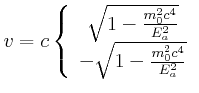
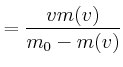 |
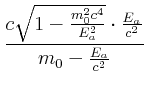 |
|||
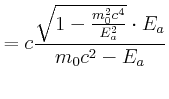 |
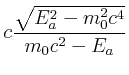 |
|||
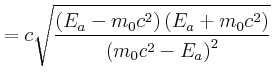 |
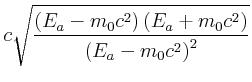 |
|||
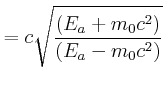 |
Impuls:
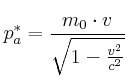
setze für
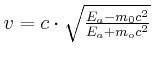 ein (siehe Teil a):
ein (siehe Teil a):
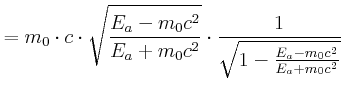 |
||
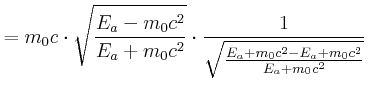 |
||
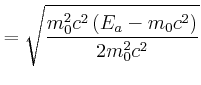 |
||
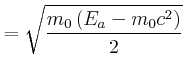 |
||
| (0.1) |
Energie:
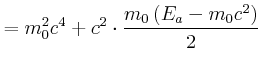 |
||
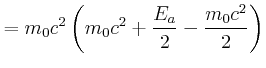 |
||
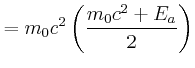 |
||
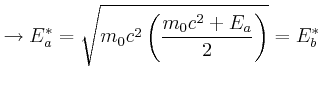 |
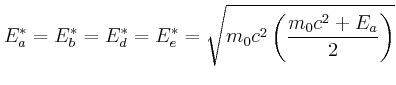
Es ist
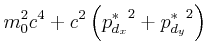 |
||||
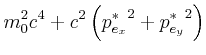 |
Betrachte zunächst den Impuls aufgespalten in ![]() - und
- und ![]() -Richtung:
-Richtung:
![]() -Richtung:
-Richtung:
![]() -Richtung:
-Richtung:
Also ist
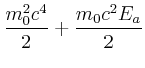 |
||||
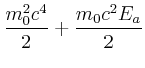 |
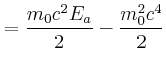 |
||
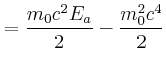 |
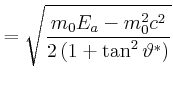 |
||
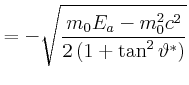 |
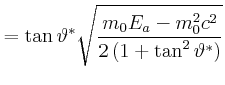 |
||
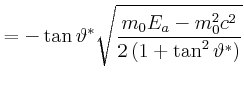 |
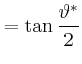 |
||
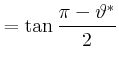 |
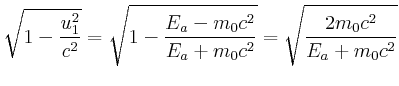
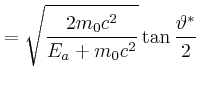 |
||
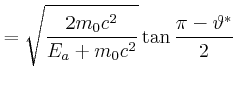 |
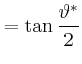 |
||||||
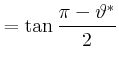 |
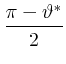 |
|||||
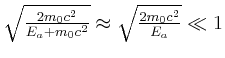 . Dann ist auch
. Dann ist auch
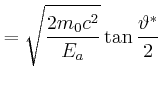 |
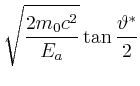 |
|||||
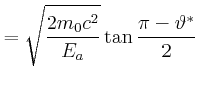 |
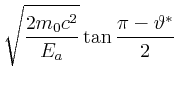 |
|||||
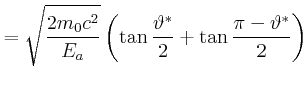 |
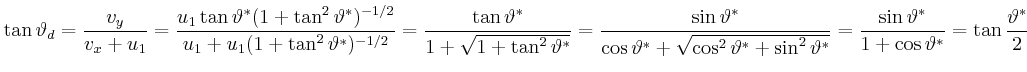
![$\displaystyle \left(
\begin{array}[c]{c}
0\\
\frac{1}{\sqrt{2}}\\
\frac{1}{...
...nd{array}\right) =T\left(
\begin{array}[c]{c}
1\\
0\\
0
\end{array}\right)
$](img285.gif)
mit
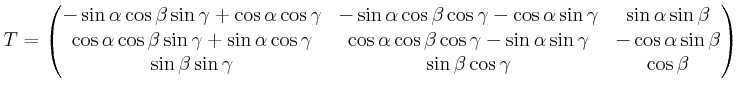
Also
![$\displaystyle \left(
\begin{array}[c]{c}
0\\
\frac{1}{\sqrt{2}}\\
\frac{1}{...
...beta\sin\gamma+\sin\alpha\cos\gamma\\
\sin\beta\sin\gamma
\end{array}\right)
$](img287.gif)
Entweder man rät die 3 Winkel ausgehend von der 3. Gleichung, oder man verwendet Maple, um das Gleichungssystem zu lösen, und erhält die Lösungen:
![$\displaystyle \left(
\begin{array}[c]{c}
\alpha\\
\beta\\
\gamma
\end{array...
...}\\
-\frac{\pi}{2}\\
-\frac{3\pi}{4}
\end{array}\right)
\end{array}\right.
$](img288.gif)
![$\displaystyle =\left( \begin{array}[c]{ccc} 0 & 0 & 1\\ \frac{1}{\sqrt{2}} & -\...
...\sqrt{2}} & 0\\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} & 0 \end{array} \right)$](img290.gif) |
||
![$\displaystyle \Rightarrow T\left( \begin{array}[c]{c} 0\\ 0\\ 1 \end{array} \right) =\left( \begin{array}[c]{c} 1\\ 0\\ 0 \end{array} \right)$](img291.gif) |
![$\displaystyle :\left( \begin{array}[c]{c} \alpha\\ \beta\\ \gamma \end{array} \right) =\left( \begin{array}[c]{c} \frac{\pi}{2}\\ 0\\ 0 \end{array} \right)$](img293.gif) |
||
![$\displaystyle :\left( \begin{array}[c]{c} \alpha\\ \beta\\ \gamma \end{array} \right) =\left( \begin{array}[c]{c} 0\\ \frac{\pi}{2}\\ 0 \end{array} \right)$](img295.gif) |
Damit ist
![$\displaystyle T_{1}=\left(
\begin{array}[c]{ccc}
0 & -1 & 0\\
1 & 0 & 0\\
0 & 0 & 1
\end{array}\right) \ $](img296.gif) und
und ![$\displaystyle T_{2}=\left(
\begin{array}[c]{ccc}
1 & 0 & 0\\
0 & 0 & -1\\
0 & 1 & 0
\end{array}\right)
$](img297.gif)
![$\displaystyle T_{1}T_{2}=\left(
\begin{array}[c]{ccc}
0 & 0 & 1\\
1 & 0 & 0\\
0 & 1 & 0
\end{array}\right)
$](img298.gif)
![$\displaystyle T_{2}T_{1}=\left(
\begin{array}[c]{ccc}
0 & -1 & 0\\
0 & 0 & -1\\
1 & 0 & 0
\end{array}\right)
$](img299.gif)
![$\displaystyle T_{1}:\left(
\begin{array}[c]{c}
\alpha\\
\beta\\
\gamma
\end...
...{2}+\gamma\text{, }\beta=\pi\text{, }\gamma=\text{beliebig}
\end{array}\right.
$](img301.gif)
und
![$\displaystyle T_{2}:\left(
\begin{array}[c]{c}
\alpha\\
\beta\\
\gamma
\end...
...ha=\text{beliebig, }\beta=-\frac{\pi}{2}\text{, }\gamma=\pi
\end{array}\right.
$](img302.gif)