Weiter: Maxwellrelationen für homogene Substanzen Oben: Wärmelehre Zurück: Extensive und intensive Variablen Skript: PDF-Datei Übungen: Blätter
| Dieser Stoff wurde am 28. 06. 2007 behandelt |
|
|
Materialien
Folien zur Vorlesung am 28. 06. 2007 PDF Übungsblatt 12 ausgegeben am 02. 07. 2007 Lösungsblatt 12 ausgegeben am 02. 07. 2007 |
Dieser Abschnitt benutzt die Differentiationsregeln für Funktionen mehrerer
Variablen. Wir betrachten eine Funktion
![]() ,
,![]() . Die in der Mathematik
übliche Schreibweise einer partiellen Ableitung
. Die in der Mathematik
übliche Schreibweise einer partiellen Ableitung
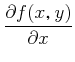 |
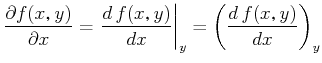 |
So ist die Wärmekapazität bei konstantem ![]() durch
durch
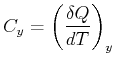 |
(4.485) |
| (4.486) |
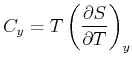 |
(4.487) |
Als Beispiel berechnen wir die Wärmekapazität bei konstantem Volumen:
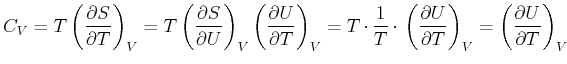 |
(4.488) |
Der 1. Hauptsatz lautet
Im Folgenden soll für ein ideales Gas
| (4.489) |
Für die innere Energie gilt allgemein:
| (4.490) |
Damit kann man das totale Differential ![]() schreiben als
schreiben als
Aus dem 1. Hauptsatz und der idealen Gasgleichung erhalten wir
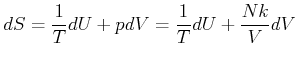 |
(4.492) |
Das totale Differential ![]() wird durch den Ausdruck aus Gleichung (4.215)
ersetzt. Wir erhalten
wird durch den Ausdruck aus Gleichung (4.215)
ersetzt. Wir erhalten
![$\displaystyle dS=\frac{1}{T}\left( \frac{\partial U}{\partial T}\right) _{V}dT+...
...c{1}{T}\left( \frac{\partial U}{\partial V}\right) _{T}+\frac{Nk} {V}\right] dV$](img2033.gif) |
(4.493) |
Da ![]() ein totales Differential ist, muss für
ein totales Differential ist, muss für
![]() ,
,![]() gelten
gelten
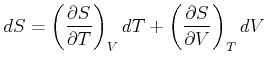 |
(4.494) |
Diese beiden Beziehungen müssen für alle ![]() und
und ![]() gelten. Deshalb müssen
die Vorfaktoren einzeln gleich sein:
gelten. Deshalb müssen
die Vorfaktoren einzeln gleich sein:
Wir betrachten nun die zweiten Ableitungen. Für gemischte Ableitungen gilt immer.
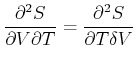 |
(4.497) |
Wenn wir bei dieser Beziehung die ersten Ableitungen der Entropie mit ihren äquivalenten Grössen einsetzen, erhalten wir
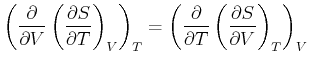 |
(4.498) |
Wir ersetzen auf der linken Seite
![]() mit Gleichung (4.219) und auf der rechten Seite
mit Gleichung (4.219) und auf der rechten Seite
![]() mit Gleichung (4.220) und erhalten
mit Gleichung (4.220) und erhalten
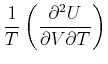 |
![$\displaystyle = \left( \frac{\partial}{\partial T}\left[\frac{1}{T}\left( \frac{\partial U}{\partial V}\right) _{T}+\frac{Nk}{V}\right]\right) _{V}$](img2048.gif) |
|
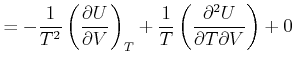 |
(4.499) |
Die Ableitung ist null (
![]() ), da
), da ![]() nicht von
nicht von ![]() abhängt.
abhängt.
Deshalb gilt
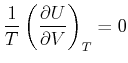 |
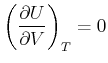 |
(4.500) |
Othmar Marti