Weiter: Allgemeine Formel für spezifische Oben: Wärmelehre Zurück: Relationen zwischen thermodynamischen Grössen Skript: PDF-Datei Übungen: Blätter
Die Maxwellrelationen sind die Konsequenz der Anwendung der Differentialrechnung auf den ersten Hauptsatz.
Die innere Energie ![]() wird als Funktion der Entropie
wird als Funktion der Entropie ![]() und des Volumens
und des Volumens ![]() angesehen.
angesehen.
| (4.502) |
![]() kann als totales Differential geschrieben werden:
kann als totales Differential geschrieben werden:
Die Gleichungen (4.225) und (4.227) beschreiben das
gleiche thermodynamische System. Da ![]() und
und ![]() beliebig wählbar sind
(unabhängige Variablen) müssen ihre Koeffizienten gleich sein:
beliebig wählbar sind
(unabhängige Variablen) müssen ihre Koeffizienten gleich sein:
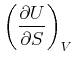 |
(4.504) | |
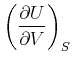 |
(4.505) |
Die gemischten zweiten Ableitungen sind unabhängig von der Reihenfolge.
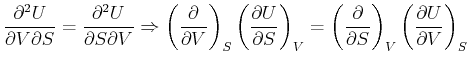 |
(4.506) |
Damit erhält man
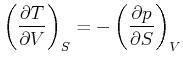 |
(4.507) |
Das betrachtete thermodynamische System soll durch die freien Variablen ![]() und
und
![]() beschrieben werden. Dies bedeutet, dass das Volumen
beschrieben werden. Dies bedeutet, dass das Volumen ![]() eine Konsequenz des
angelegten Druckes
eine Konsequenz des
angelegten Druckes ![]() sein soll. Das Differential
sein soll. Das Differential ![]() ausgerechnet ist
ausgerechnet ist
| (4.508) |
Umgestellt erhalten wir
| (4.509) |
![]() wird links und rechts addiert
wird links und rechts addiert
| (4.510) |
Wir definieren die Enthalpie ![]()
| (4.511) |
Analog zum ersten Hauptsatz erhalten wir mit den unabhängigen Variablen ![]() und
und
![]()
| (4.512) |
Andererseits kann ![]() als totales Differential geschrieben werden
als totales Differential geschrieben werden
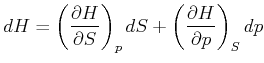 |
(4.513) |
Der Koeffizientenvergleich ergibt die beiden Beziehungen
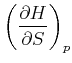 |
(4.514) | |
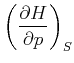 |
(4.515) |
Wieder sind die gemischten zweiten Ableitungen unabhängig von der Reihenfolge.
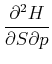 |
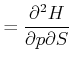 |
Damit erhalten wir die Beziehung
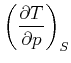 |
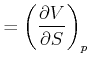 |
(4.516) |
Das betrachtete thermodynamische System soll durch die freien Variablen ![]() und
und
![]() beschrieben werden. Dies bedeutet, dass die Entropie
beschrieben werden. Dies bedeutet, dass die Entropie ![]() eine Konsequenz
der herrschenden Temperatur
eine Konsequenz
der herrschenden Temperatur ![]() sein soll. Das Differential
sein soll. Das Differential ![]() ausgerechnet ist
ausgerechnet ist
| (4.517) |
Umgestellt erhalten wir
| (4.518) |
![]() wird links und rechts subtrahiert
wird links und rechts subtrahiert
| (4.519) |
Wir nennen die Grösse
| (4.520) |
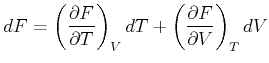 |
(4.521) |
Der Koeffizientenvergleich ergibt die beiden Beziehungen
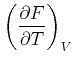 |
(4.522) | |
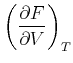 |
(4.523) |
Die Reihenfolge der gemischten zweiten Ableitungen kann vertauscht werden.
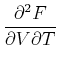 |
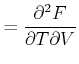 |
Damit erhalten wir die Beziehungen
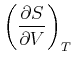 |
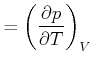 |
(4.524) |
Das betrachtete thermodynamische System soll durch die freien Variablen ![]() und
und
![]() beschrieben werden. Dies bedeutet, dass die Entropie
beschrieben werden. Dies bedeutet, dass die Entropie ![]() eine Konsequenz
der herrschenden Temperatur
eine Konsequenz
der herrschenden Temperatur ![]() und das Volumen
und das Volumen ![]() durch den Druck
durch den Druck ![]() bestimmt sein soll. Wir addieren nun im ersten Hauptsatz auf beiden Seiten
bestimmt sein soll. Wir addieren nun im ersten Hauptsatz auf beiden Seiten
![]() und erhalten
und erhalten
| (4.525) |
Wir nennen die Grösse
| (4.526) |
die freie Enthalpie oder die Gibbssche freie Energie. ![]() ist ein totales
Differential
ist ein totales
Differential
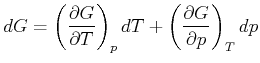 |
(4.527) |
Durch Koeffizientenvergleich erhält man
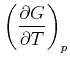 |
(4.528) | |
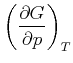 |
(4.529) |
Die Reihenfolge der gemischten zweiten Ableitungen kann gewechselt werden.
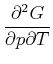 |
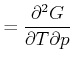 |
Damit erhalten wir die Beziehung
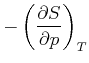 |
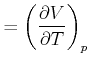 |
(4.530) |
| Dieser Stoff wurde am 02. 07. 2007 behandelt |
|
|
Materialien
Folien zur Vorlesung am 02. 07. 2007 PDF |
Die vier aus den zweiten Ableitungen der thermodynamischen energetischen
Zustandsfunktionen ![]() ,
, ![]() ,
, ![]() , und
, und ![]() abgeleiteten Beziehungen heissen
Maxwellrelationen.
abgeleiteten Beziehungen heissen
Maxwellrelationen.
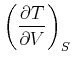 |
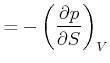 |
(4.531) |
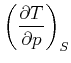 |
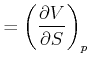 |
(4.532) |
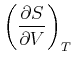 |
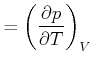 |
(4.533) |
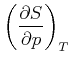 |
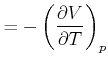 |
(4.534) |
Die vier Maxwellrelationen folgen alle aus der Tatsache, dass die Anzahl zugänglicher Zustände eines thermodynamischen Systems dieses System beschreibt (in der Quantenmechanik eindeutig, sonst bis auf eine additive Konstante der Entropie).
![]() ,
, ![]() ,
, ![]() und
und ![]() heissen thermodynamische Potentiale.
Dieser Begriff ist verwirrend, da anders als im Rest der Physik diese Grössen
die Einheit einer Energie haben.
heissen thermodynamische Potentiale.
Dieser Begriff ist verwirrend, da anders als im Rest der Physik diese Grössen
die Einheit einer Energie haben.
![\includegraphics[width=0.7\textwidth]{relationen-001}](img2124.gif)
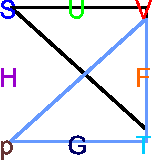
Eselsbrücke für thermodynamische Potentiale
|
Die thermodynamischen Potentiale stehen in dieser Darstellung in der Mitte der
Quadrate. Die unabhängigen Variablen sind immer die benachbart zu dem
jeweiligen Potential. So steht ![]() zwischen
zwischen ![]() und
und ![]() .
.
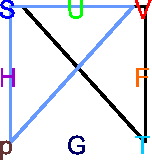
Die Maxwellrelation
|
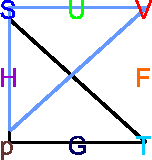
Die Maxwellrelation
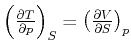 . .
|
Die Maxwellrelation
|
Die
Maxwellrelation
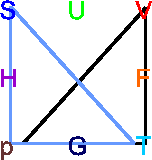
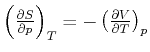 . Hier zeigen die Spitzen der
Dreiecke nach oben, und wir haben ein Minuszeichen in der Relation. . Hier zeigen die Spitzen der
Dreiecke nach oben, und wir haben ein Minuszeichen in der Relation.
|
Bei der Berechnung der Eigenschaften der inneren Energie ![]() hatten wir festgestellt, dass im Gleichgewicht die
Entropie
hatten wir festgestellt, dass im Gleichgewicht die
Entropie ![]() maximal und die innere Energie
maximal und die innere Energie ![]() minimal ist. Dabei war immer die Nebenbedingung, dass das System
von der Umwelt isoliert sei, das heisst dass
minimal ist. Dabei war immer die Nebenbedingung, dass das System
von der Umwelt isoliert sei, das heisst dass
![]() war (adiabatische Prozesse), und dass das Volumen
konstant war,
war (adiabatische Prozesse), und dass das Volumen
konstant war, ![]() (isochore Prozesse). In diesem Kapitel interessieren wir uns für die
Gleichgewichtsbedingungen, wenn andere Randbedingungen als
(isochore Prozesse). In diesem Kapitel interessieren wir uns für die
Gleichgewichtsbedingungen, wenn andere Randbedingungen als
![]() und
und ![]() gelten.
gelten.
![\includegraphics[width=0.4\textwidth]{thermodynamik-000}](img2130.gif)
Links ist das Feder-Masse-Pendel ohne Gravitationsfeld zu
sehen, rechts mit Gravitationsfeld.
|
Ein Feder-Masse-Pendel wird durch die Federkraft
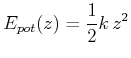 |
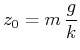 |
![\includegraphics[width=0.7\textwidth]{thermodynamik-F00}](img2136.gif)
|
Abbildung 4.49 zeigt, wie das Anschalten der Gravitation den Ort des Minimums verändert. Wenn also die Nebenbedingungen (manchmal auch Randbedingungen genannt) ändern, so ändert sich die Gleichgewichtslage. Wir wollen im Folgenden untersuchen, wie andere als die adiabatisch-isochoren Randbedingungen die Gleichgewichtslage ändern.
Um klar abzugrenzen, welche Randbedingungen angewendet werden, wenn die Gleichgewichtslage gesucht wird, wird für jedes Paar von Randbedingungen eine andere Energie definiert. Diese Energiefunktionen werden thermodynamische Potentiale genannt. So würde man ja auch
Jedes System, das nicht adiabatisch ist, erlaubt den Wärmeaustausch mit der Umgebung. Um die Gleichgewichtsbedingungen zu finden, müssen wir deshalb das System und die Umgebung gemeinsam betrachten! Bei einem offenen System ist die Entropie
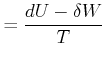 |
||
Hierbei wird angenommen, dass nur mechanische Arbeit möglich ist. Also ist
Wenn das Volumen zwangsweise konstant gehalten wird, entfällt die Druckarbeit
![]() . Wenn weiter auch die Temperatur konstant gehalten wird, ist
. Wenn weiter auch die Temperatur konstant gehalten wird, ist ![]() .
Diese Grösse kann also subtrahiert werden. Gleichung (4.263) wird dann
.
Diese Grösse kann also subtrahiert werden. Gleichung (4.263) wird dann
|
Bei isotherm-isochoren Bedingungen ( minimal. |
Wenn ![]() und
und ![]() konstant sind, kann man Gleichung (4.263) durch
konstant sind, kann man Gleichung (4.263) durch
![]() und
und ![]() ergänzen und erhält
ergänzen und erhält
|
Bei isotherm-isobaren Bedingungen ( minimal. |
Ohne Wärmeaustausch ist ![]() . Wenn gleichzeitig der Druck
. Wenn gleichzeitig der Druck ![]() konstant
ist, entfällt in Gleichung (4.263) der Term
konstant
ist, entfällt in Gleichung (4.263) der Term ![]() und wir können
und wir können
![]() addieren.
addieren.
|
Bei adiabatisch-isobaren Bedingungen (
minimal. |
Adiabatisch-isobare Bedingungen können mit einem Dewar-Gefäss (thermisch isoliert) mit einem beweglichen Deckel
der Masse ![]() im Gravitationsfeld simuliert werden. Wäre der Deckel fixiert, hätten wir die adiabatisch isochoren
Bedingungen, die ein Minimum der inneren Energie
im Gravitationsfeld simuliert werden. Wäre der Deckel fixiert, hätten wir die adiabatisch isochoren
Bedingungen, die ein Minimum der inneren Energie ![]() fordern. Beim beweglichen Deckel liegt die Gleichgewichtslage
anders, wie aus dem Beispiel mit dem Feder-Masse-Pendel im Gravitationsfeld (Abbildung 4.49) zu
ersehen ist. Die Gleichgewichtslage ist nun durch die kombinierte Energie bestehend aus der inneren Energie und
der Gravitationsenergie gegeben!
fordern. Beim beweglichen Deckel liegt die Gleichgewichtslage
anders, wie aus dem Beispiel mit dem Feder-Masse-Pendel im Gravitationsfeld (Abbildung 4.49) zu
ersehen ist. Die Gleichgewichtslage ist nun durch die kombinierte Energie bestehend aus der inneren Energie und
der Gravitationsenergie gegeben!
Schliesslich entfällt in Gleichung (4.263) sowohl ![]() wie auch
wie auch
![]() , wenn das Volumen
, wenn das Volumen ![]() konstant gehalten wird und kein
Energieaustausch
konstant gehalten wird und kein
Energieaustausch
![]() vorkommt.
vorkommt.
|
Bei adiabatisch-isochoren Bedingungen (
minimal. |
Je nach den Bedingungen (isobar, isotherm, usw) kann man mit dem entsprechenden thermodynamischen Potential den Reaktionsweg und die Reaktionsrichtung bestimmen.
Othmar Marti