



Next: Zusammenfassung
Up: Elektromagnetische Wellen
Previous: Poynting-Vektor und Energiefluss
Hier soll mit einer beschleunigten Ladung erklärt werden, wie Wellen im Raum entstehen.
Versuch zur Vorlesung: Hertzscher Dipol SW099
Versuch zur Vorlesung: Stehende Wellen SW032
Wir betrachten eine Ladung 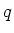 , die die folgende Geschwindigkeit hat
, die die folgende Geschwindigkeit hat
Die Beschleunigungszeit 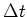 sowie die Beschleunigung
sowie die Beschleunigung 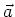 sollen so gewählt sein, dass
sollen so gewählt sein, dass
gilt. Die Behauptung ist, dass das elektrische Feld 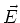 für
für
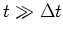 wie in der Zeichnung oben
aussieht. In der Beschleunigungsphase soll eine elektromagnetische Welle erzeugt worden sein. Ausserhalb der Kugel
mit dem radius
wie in der Zeichnung oben
aussieht. In der Beschleunigungsphase soll eine elektromagnetische Welle erzeugt worden sein. Ausserhalb der Kugel
mit dem radius
muss das elektrische Feld das Feld einer im Ursprung ruhenden Ladung sein, da nach der
Relativitätstheorie die Information über die Beschleunigung diesen Raum noch nicht erreicht haben kann.
Innerhalb der Kugel mit
haben wir das Feld der Ladung 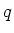 , die sich mit der konstanten Geschwindigkeit
, die sich mit der konstanten Geschwindigkeit 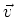 bewegt, denn in diesem
Bereich ist die Welle, so wir eine erzeugt haben, schon wieder vorbei. Die Feldlinien im Laborsystem können wir
erhalten, indem wir das elektrische Feld im Ruhesystem der Ladung (radiale Feldlinien) in das Laborsystem
transformieren. Wenn
bewegt, denn in diesem
Bereich ist die Welle, so wir eine erzeugt haben, schon wieder vorbei. Die Feldlinien im Laborsystem können wir
erhalten, indem wir das elektrische Feld im Ruhesystem der Ladung (radiale Feldlinien) in das Laborsystem
transformieren. Wenn 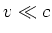 ist, haben wir auch im Laborsystem radiale Feldlinien, die von der momentanen
Position der Ladung weggehen. Die Maxwellgleichung im Vakuum
ist, haben wir auch im Laborsystem radiale Feldlinien, die von der momentanen
Position der Ladung weggehen. Die Maxwellgleichung im Vakuum
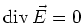 bedingt, dass die Feldlinien
geschlossen und stetig sind. Die Vermutung ist, dass die Feldlinien in der Wellenzone linear die beiden
Feldlinienmuster miteinander verbinden.
bedingt, dass die Feldlinien
geschlossen und stetig sind. Die Vermutung ist, dass die Feldlinien in der Wellenzone linear die beiden
Feldlinienmuster miteinander verbinden.
|
Berechnung der Wellenausbreitung
|
Da
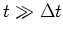 ist, kann die Beschleunigungsphase für die Bestimmung der Position der Ladung zur Zeit
ist, kann die Beschleunigungsphase für die Bestimmung der Position der Ladung zur Zeit 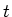 vernachlässigt werden. Wir haben also
vernachlässigt werden. Wir haben also
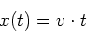 |
(6.33) |
Wegen 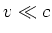 ist dann auch
ist dann auch
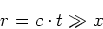 |
(6.34) |
sowie wegen
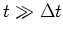 auch
auch
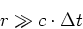 |
(6.35) |
Wir bezeichnen mit 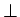 die Richtung senkrecht zum Radiusvektor
die Richtung senkrecht zum Radiusvektor 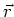 . Wir erhalten dann, unter der Annahme,
dass das
. Wir erhalten dann, unter der Annahme,
dass das 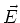 -Feld in der Wellenzone linear sei,
-Feld in der Wellenzone linear sei,
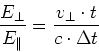 |
(6.36) |
Mit
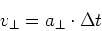 |
(6.37) |
sowie mit 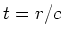 bekommen wir
bekommen wir
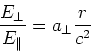 |
(6.38) |
Andererseits, wenn wir die Integralform der ersten Maxwellgleichung auf den kleinen Zylinder an der Stelle 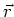 anwenden, erhalten
anwenden, erhalten
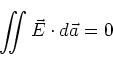 |
(6.39) |
und damit mit dem Coulombgesetz
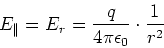 |
(6.40) |
Dies bedeutet, dass das radiale 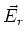 -Feld sich stetig durch die Kugelschale hindurch fortsetzt. Die
Komponente
-Feld sich stetig durch die Kugelschale hindurch fortsetzt. Die
Komponente 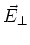 existiert nur in der Wellenzone. Das
existiert nur in der Wellenzone. Das 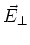 -Feld ist das gesuchte Feld der
elektromagnetischen Feldes, das Strahlungsfeld. Seine Grösse ist
-Feld ist das gesuchte Feld der
elektromagnetischen Feldes, das Strahlungsfeld. Seine Grösse ist
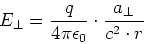 |
(6.41) |
Vektoriell geschrieben lautet diese Gleichung
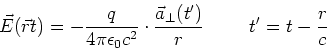 |
(6.42) |
Das elektrische Feld 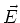 an der Stelle
an der Stelle 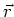 ist proportional zur senkrechten Komponente der
Beschleunigung, aber zur retardierten Zeit
ist proportional zur senkrechten Komponente der
Beschleunigung, aber zur retardierten Zeit 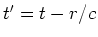 . Zum Strahlungsfeld gehört auch
ein
. Zum Strahlungsfeld gehört auch
ein 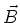 -Feld, das so gerichtet ist, dass
-Feld, das so gerichtet ist, dass 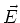 ,
, 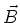 und
und 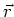 ein Rechtssystem bilden.
ein Rechtssystem bilden. 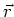 ist die Ausbreitungsrichtung. Das Magnetfeld ist, in vektorieller Schreibweise,
ist die Ausbreitungsrichtung. Das Magnetfeld ist, in vektorieller Schreibweise,
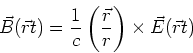 |
(6.43) |
Wenn wir 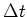 halbieren, bleibt der äussere Teil der des Strahlungsfeldes konstant, der innere Teil liegt
dann in der Mitte der Verbindungslinie durch die Wellenzone. Durch fortgesetzte Anwendung dieses Verfahrens wird
die Linearität des elektrischen Feldes in der Wellenzone gezeigt.
halbieren, bleibt der äussere Teil der des Strahlungsfeldes konstant, der innere Teil liegt
dann in der Mitte der Verbindungslinie durch die Wellenzone. Durch fortgesetzte Anwendung dieses Verfahrens wird
die Linearität des elektrischen Feldes in der Wellenzone gezeigt.
Ein Elektron in einem Atom führe in die 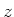 -Richtung die harmonische Bewegung
-Richtung die harmonische Bewegung
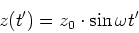 |
(6.44) |
durchführt. Dabei ist 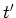 die retardierte Zeit. Die Beschleunigung ist
die retardierte Zeit. Die Beschleunigung ist
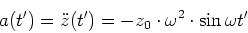 |
(6.45) |
Das elektrische Feld ist
![\begin{displaymath}
E(r,\Theta,t) = \frac{e}{4\pi \epsilon_0 c^2}\cdot\frac{1}{...
...dot\sin\left[\omega\left(t-\frac{r}{c}\right)\right]\sin\Theta
\end{displaymath}](img1418.gif) |
(6.46) |
Das Magnetfeld ist
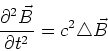 |
(6.47) |
Der Poynting-Vektor oder Energiefluss ist
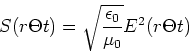 |
(6.48) |
Mit
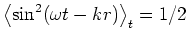 wird die Intensität
wird die Intensität
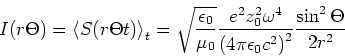 |
(6.49) |
Damit haben wir gezeigt, dass die Annahme eines harmonischen Oszillators das Strahlungsfeld eines Atoms erklären
kann. Die abgeführte Energie dämpft dabei den Oszillator. Je stärker die Dämpfung ist, das heisst, je kürzer die
Lebensdauer ist, desto breiter wird das Frequenzspektrum sein.




Next: Zusammenfassung
Up: Elektromagnetische Wellen
Previous: Poynting-Vektor und Energiefluss
Othmar Marti
Experimentelle Physik
Universiät Ulm
![\includegraphics[width=0.8\textwidth]{em-wellen-007.eps}](img1389.gif)
![]() , die die folgende Geschwindigkeit hat
, die die folgende Geschwindigkeit hat

![]() sowie die Beschleunigung
sowie die Beschleunigung ![]() sollen so gewählt sein, dass
sollen so gewählt sein, dass
![\includegraphics[width=0.5\textwidth]{em-wellen-008.eps}](img1397.gif)
![]() ist, kann die Beschleunigungsphase für die Bestimmung der Position der Ladung zur Zeit
ist, kann die Beschleunigungsphase für die Bestimmung der Position der Ladung zur Zeit ![]() vernachlässigt werden. Wir haben also
vernachlässigt werden. Wir haben also
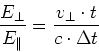
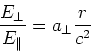
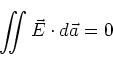
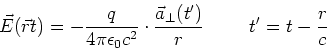
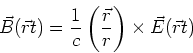
![]() halbieren, bleibt der äussere Teil der des Strahlungsfeldes konstant, der innere Teil liegt
dann in der Mitte der Verbindungslinie durch die Wellenzone. Durch fortgesetzte Anwendung dieses Verfahrens wird
die Linearität des elektrischen Feldes in der Wellenzone gezeigt.
halbieren, bleibt der äussere Teil der des Strahlungsfeldes konstant, der innere Teil liegt
dann in der Mitte der Verbindungslinie durch die Wellenzone. Durch fortgesetzte Anwendung dieses Verfahrens wird
die Linearität des elektrischen Feldes in der Wellenzone gezeigt.
![]() -Richtung die harmonische Bewegung
-Richtung die harmonische Bewegung