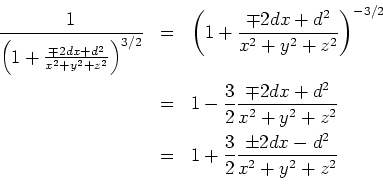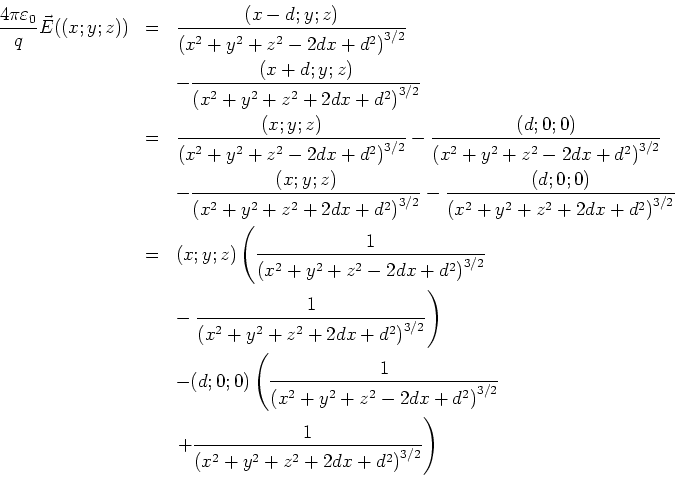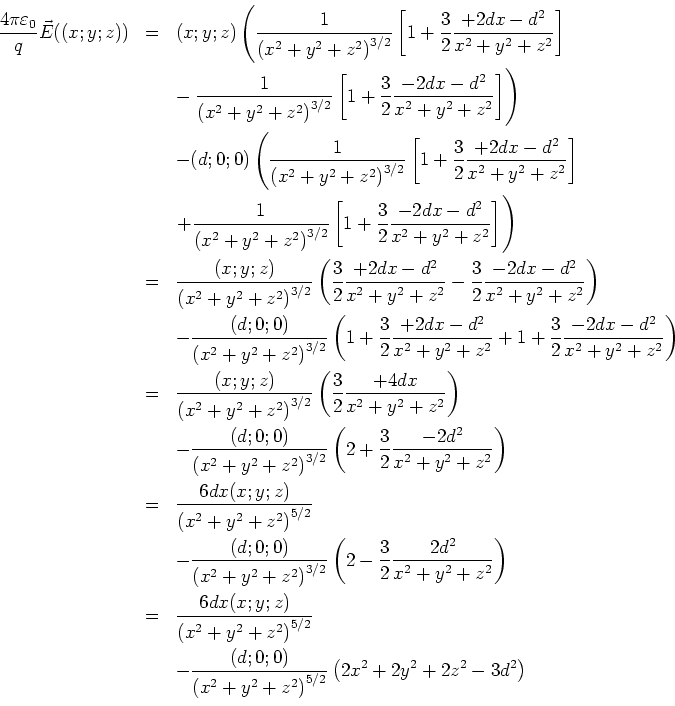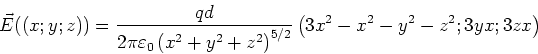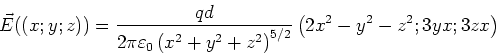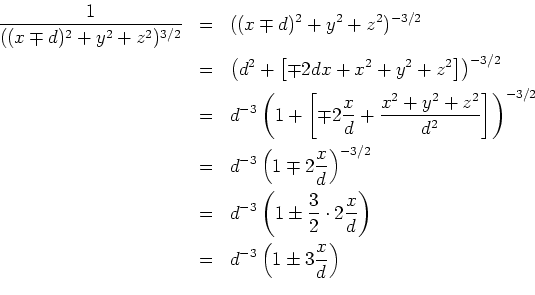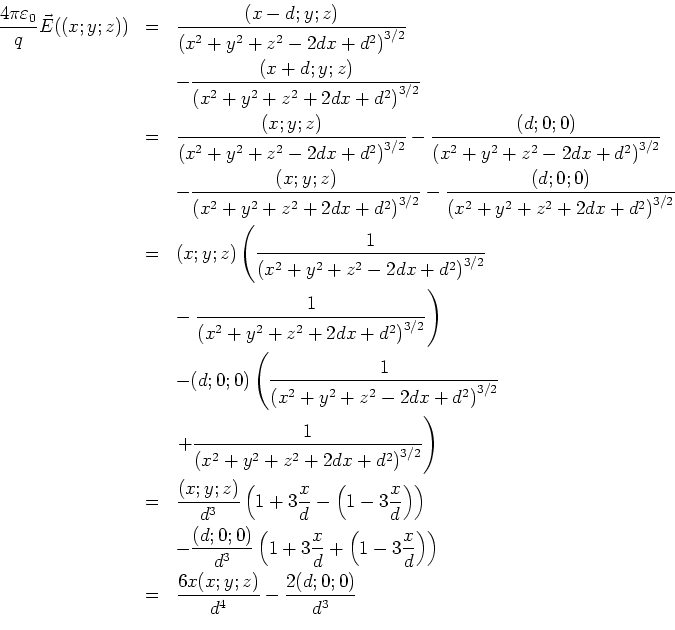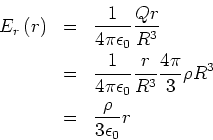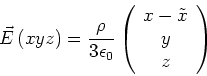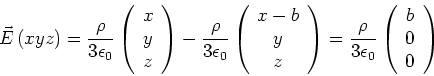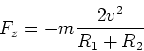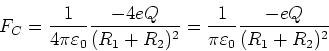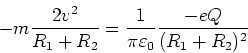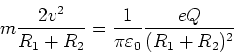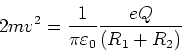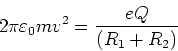

Up: PHYS3100 Grundkurs IIIb
Übungsblatt 02
PHYS3100 Grundkurs IIIb (Physik, Wirtschaftsphysik, Physik Lehramt)
Othmar Marti, (othmar.marti@physik.uni-ulm.de)
3. 11. 2003 oder 10. 11. 2003
- Eine Kugel mit dem Radius
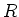 hat im Inneren eine Ladungsverteilung wie
hat im Inneren eine Ladungsverteilung wie
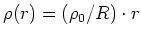 . Berechnen Sie das elektrische
Feld
. Berechnen Sie das elektrische
Feld 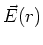 und das elektrostatische Potential
und das elektrostatische Potential 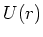 für
für
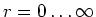 .
.
- Zeigen Sie, analog zum Gravitationsfeld, dass die Coulombkraft ein konservatives Kraftfeld ist.
- Zwei vom Betrage her gleich grosse Ladungen,
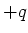 und
und 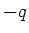 , befinden sich an den Orten
, befinden sich an den Orten
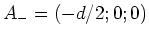 und
und
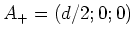 . Berechnen Sie
. Berechnen Sie
 . Geben Sie eine Näherung bis zur ersten nichttrivialen Ordnung
für
. Geben Sie eine Näherung bis zur ersten nichttrivialen Ordnung
für
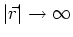 an. Geben Sie eine Näherung bis zur ersten nichttrivialen Ordnung für
an. Geben Sie eine Näherung bis zur ersten nichttrivialen Ordnung für
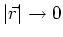 an.
an.
- Eine nichtleitende Kugel mit dem Radius
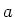 und dem Mittelpunkt im Ursprung habe einen kugelförmigen
Hohlraum mit dem Radius
und dem Mittelpunkt im Ursprung habe einen kugelförmigen
Hohlraum mit dem Radius 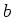 und dem Mittelpunkt bei
und dem Mittelpunkt bei 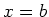
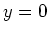 und
und 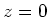 . Die Kugel besitze die homogene
Raumladungsdichte
. Die Kugel besitze die homogene
Raumladungsdichte 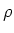 . Zeigen Sie, dass das elektrische Feld im Hohlraum homogen ist und durch
. Zeigen Sie, dass das elektrische Feld im Hohlraum homogen ist und durch
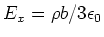 sowie
sowie 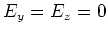 beschrieben wird. Hinweis: Ersetzen Sie den Hohlraum durch
Kugeln mit gleich grossen positiven und negativen Ladungsdichten.
beschrieben wird. Hinweis: Ersetzen Sie den Hohlraum durch
Kugeln mit gleich grossen positiven und negativen Ladungsdichten.
![\includegraphics[height=0.25\textwidth]{ue-02-03.eps}](img21.gif)
- Gegeben seien zwei konzentrische Kugeln mit den Radien
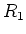 und
und 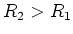 . Ein Elektron werde im
gleichen Abstand vom inneren und vom äusseren Zylinder, also bei
. Ein Elektron werde im
gleichen Abstand vom inneren und vom äusseren Zylinder, also bei 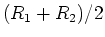 mit der Geschwindigkeit
mit der Geschwindigkeit 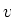 tangential zu den Kugeln eingeschossen. Beide Kugeloberflächen tragen Ladungen, die vom Betrage her
gleich sind. Wie gross müssen die Ladungen auf dem inneren und auf dem äusseren Kugel sein, damit das
Elektron eine geschlossene Kreisbahn beschreibt?
tangential zu den Kugeln eingeschossen. Beide Kugeloberflächen tragen Ladungen, die vom Betrage her
gleich sind. Wie gross müssen die Ladungen auf dem inneren und auf dem äusseren Kugel sein, damit das
Elektron eine geschlossene Kreisbahn beschreibt?
- Wir berechnen die Lösung innerhalb der Kugel verwenden die Gleichung
oder
Das gestellte Problem ist kugelsymmetrisch, also muss auch die Lösung kugelsymmetrisch sein.
Das erste Integral ergibt (da 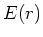 über der ganzen Kugeloberfläche konstant ist)
über der ganzen Kugeloberfläche konstant ist)
Das zweite Integral ergibt
Damit bekommen wir
Vektoriell geschrieben bekommen wir
Ausserhalb der Kugel gilt das Coulombsche Gesetz
Zusammen
Das elektrostatische Potential ist (Kugelsymmetrie)
Innerhalb der Kugel erhalten wir
Zusammen
- Coulombkraft
- Ein Kraftfeld ist konservativ, wenn
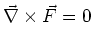 ist.
ist.
- Zu zeigen ist
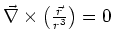
- Wir berechnen
- also
und zyklisch
- In Kugelkoordination ist
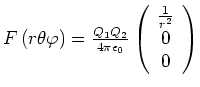
- Die Rotation in Kugelkoordinaten ist:
- da
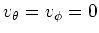 ist folgt sofort die Behauptung.
ist folgt sofort die Behauptung.
- Das gesamte elektrostatische Potential am Ort
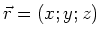 ist
ist
Wir klammern 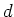 im Nenner aus
im Nenner aus
Für
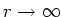 kann
kann
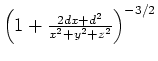 entwickelt werden.
entwickelt werden.
Wir setzen weiter
Zusammen erhalten wir also
oder
Für
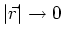 ist
ist 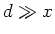 ,
, 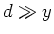 und
und 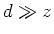 . Wir linearisieren
. Wir linearisieren
Also bekommen wir
- Die Kugel mit Hohlraum kann durch Überlagerung einer Kugel mit Radius
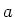 , zentriert um
, zentriert um 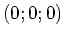 und
der Ladungsdichte
und
der Ladungsdichte 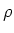 sowie einer Kugel mit dem Radius
sowie einer Kugel mit dem Radius 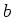 zentriert auf
zentriert auf 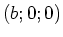 mit der Ladungsdichte
mit der Ladungsdichte
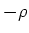 erzeugt werden.
erzeugt werden.
- E-Feld im Inneren einer homogen geladenen Kugel
- x,y,z-Komponenten des elektrischen Feldes einer Kugel mit Mittelpunkt
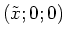
-
- In unserem Falle ist innerhalb der kleinen Kugel:
was zu zeigen war.
- Die Ladung auf der inneren Kugeloberfläche kann durch eine Punktladung
 beschrieben werden. Die Ladung
der äusseren Kugelschale trägt nichts zum Feld bei. Die Bahngeometrie verlangt eine Zentripetalkraft
beschrieben werden. Die Ladung
der äusseren Kugelschale trägt nichts zum Feld bei. Die Bahngeometrie verlangt eine Zentripetalkraft
die durch die Coulombkraft gegeben ist
Gleichsetzen
und damit
Übungsblatt 02
PHYS3100 Grundkurs IIIb (Physik, Wirtschaftsphysik, Physik Lehramt)
This document was generated using the
LaTeX2HTML translator Version 99.2beta8 (1.46)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html uebungsblatt02
The translation was initiated by marti on 2004-01-16


Up: PHYS3100 Grundkurs IIIb
Othmar Marti
Experimentelle Physik
Universiät Ulm
![\includegraphics[height=0.25\textwidth]{ue-02-03.eps}](img21.gif)
![\includegraphics[height=0.25\textwidth]{ue-02-03.eps}](img21.gif)
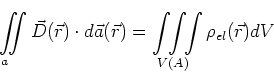
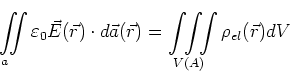
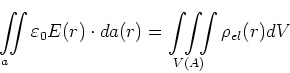
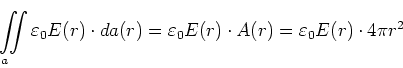
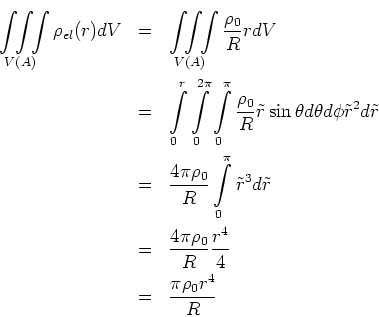
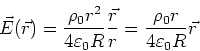
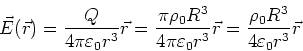
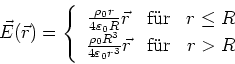
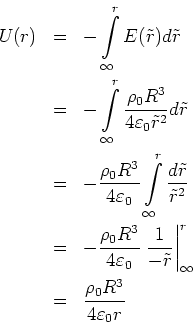
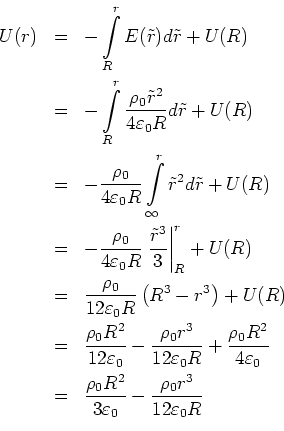
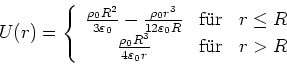
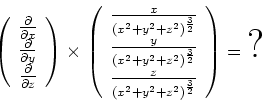
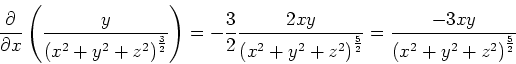
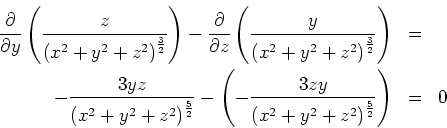
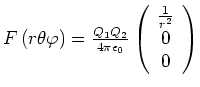
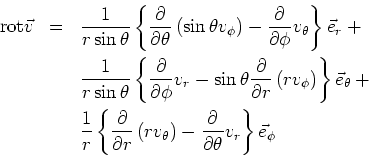
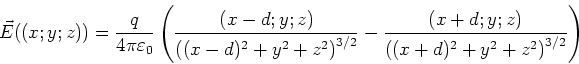
![\begin{eqnarray*}
\vec E((x;y;z)) &=& \frac{q}{4\pi\varepsilon_0
}\left(\frac{...
...\left(1+\frac{2dx+d^2}{x^2+y^2+z^2}\right)\right]^{3/2}}\right)
\end{eqnarray*}](img51.gif)
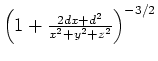 entwickelt werden.
entwickelt werden.