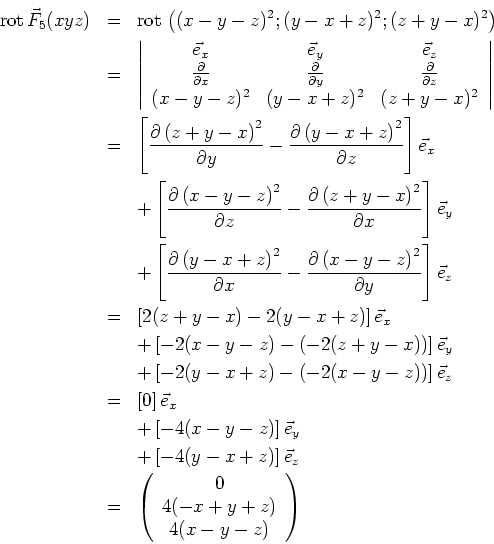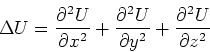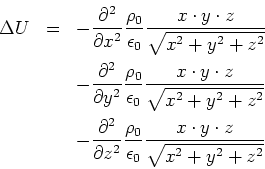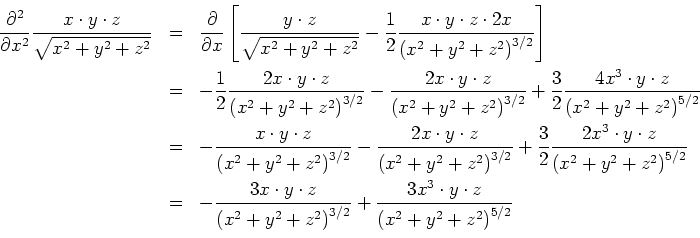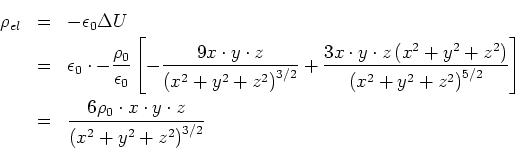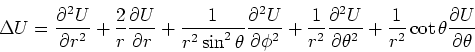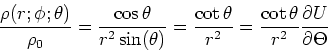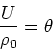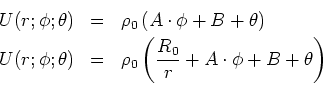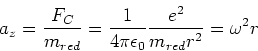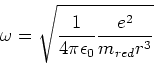

Up: PHYS3100 Grundkurs IIIb
Übungsblatt 03
PHYS3100 Grundkurs IIIb (Physik, Wirtschaftsphysik, Physik Lehramt
Othmar Marti, (othmar.marti@physik.uni-ulm.de)
17. 11. 2003 oder 24. 11. 2003
- Berechnen Sie, unter Vernachlässigung von Randeffekten, die Kapazität zwischen der obersten und der untersten
Platte der in der Skizze gezeigten
Anordnung. Die kleinen Platten zwischen den Randplatten sind isoliert.
![\includegraphics[width=0.7\textwidth]{ue-03-01a.eps}](img1.gif)
- Berechnen Sie die Kapazität einer leitfähigen Hohlkugel mit dem Radius
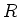 .
.
- Welche der Vektorfelder sind konservativ?
-
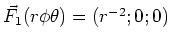
-
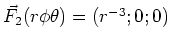
-
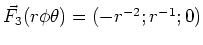
-
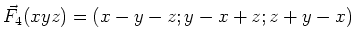
-
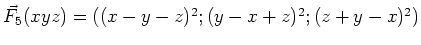
wobei die sphärischen Koordinaten durch
definiert seien. Beachten sie, dass die Definition sphärischer Koordinaten in Maple
(Hilfekapitel ''coords'' und im Bronstein nicht konsistent sind.
- Berechnen Sie zu dem Potential
die dazugehörige Ladungsverteilung und das elektrische Feld.
- Berechnen Sie das (die?) zur Ladungsverteilung
gehörige Potential.
- Berechnen Sie die klassische Umlaufszeit eines Elektrons um ein Proton, wenn der Durchmesser des
Wasserstoffatoms
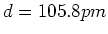 ist. Was könnte bei dieser Betrachtung des Wasserstoffatoms falsch sein?
ist. Was könnte bei dieser Betrachtung des Wasserstoffatoms falsch sein?
- Die Kapazität eines Kondensators beträgt
Unsere Schaltung sieht formal, bei Vernachlässigung der Randeffekte, wie
![\includegraphics[width=0.5\textwidth]{ue-03-02a.eps}](img13.gif)
aus. Die resultierende Kapazität aus den Serien- und Parallelschaltungen ist
Wenn
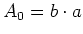 die Deckfläche ist, dann haben die Kondensatoren
die Deckfläche ist, dann haben die Kondensatoren 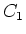 und
und 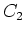 die Fläche
die Fläche
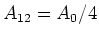 . Die Kondensatoren
. Die Kondensatoren 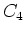 und
und 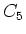 haben die Fläche
haben die Fläche
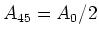 . Schliesslich hat
. Schliesslich hat
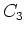 die Fläche
die Fläche 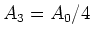 .
Wir bekommen als Werte
.
Wir bekommen als Werte
- Wenn die Ladung
 ist, ist das radiale elektrische Feld für
ist, ist das radiale elektrische Feld für 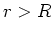
und das Potential (mit 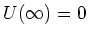 )
)
Die Definition der Kapazität ist
also
- Die Rotation in kartesischen Koordinaten ist als Determinante
gegeben. In sphärischen Koordinaten lautet die Rotation
- Wegen
ist die Funktion konservativ.
- Wegen
ist die Funktion konservativ.
- Wegen
ist die Funktion nicht konservativ.
- Wegen
ist die Funktion konservativ.
- Wegen
ist die Funktion nicht konservativ.
- Wir verwenden
oder
Nun ist
Wir setzen 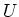 ein
ein
Da die Funktion in 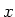 ,
,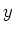 ,
, 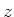 symmetrisch ist berechnen wir nur
symmetrisch ist berechnen wir nur
Alle drei Komponenten zusammen ergeben (Vorzeichen!)
- Wir verwenden den Laplace-Operator in Kugelkoordinaten.
Wir verwenden, dass der Laplace-Operator linear ist. Betrachten wir nur den Term mit
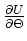 dann muss
dann muss
sein.
Also muss
sein. Der Term mit
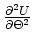 ist mit dieser Wahl identisch null. Also ist
ist mit dieser Wahl identisch null. Also ist
eine Lösung des Problems.
Allgemein kann noch eine radiale Funktion, für die
ist addiert werden. Wir setzen an, dass 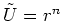 ist.
ist.
Also muss
sein. Es gibt zwei Lösungen, 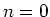 und
und 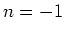 .
Der dritte Summand des Laplaceoperators ist null, wenn
.
Der dritte Summand des Laplaceoperators ist null, wenn
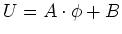 ist. Zusammen haben wir also die Lösungen
ist. Zusammen haben wir also die Lösungen
- Wir rechnen ohne Berücksichtigung der Vorzeichen. Die Geometrie der Bahn bedingt die Zentripetalbeschleunigung
Die physikalische Ursache der Zentripetalbeschleunigung ist die Coulombkraft
Wir verwenden die reduzierte masse, da es sich hier um ein Zweikörperproblem handelt. Umgestellt
und mit
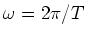
Die Masse des Elektrons ist
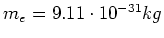 . Die Protonenmasse ist
. Die Protonenmasse ist
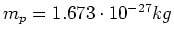 . Die reduzierte Masse ist dann
. Die reduzierte Masse ist dann
Also ist
Übungsblatt 03
PHYS3100 Grundkurs IIIb (Physik, Wirtschaftsphysik, Physik Lehramt
This document was generated using the
LaTeX2HTML translator Version 99.2beta8 (1.46)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html uebungsblatt03
The translation was initiated by marti on 2003-11-25

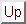

Up: PHYS3100 Grundkurs IIIb
Othmar Marti
Experimentelle Physik
Universiät Ulm
![\includegraphics[width=0.7\textwidth]{ue-03-01a.eps}](img1.gif)
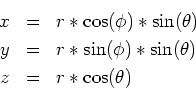
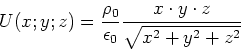
![\includegraphics[width=0.7\textwidth]{ue-03-01a.eps}](img1.gif)
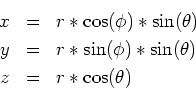
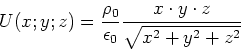
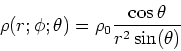
![\includegraphics[width=0.5\textwidth]{ue-03-02a.eps}](img13.gif)
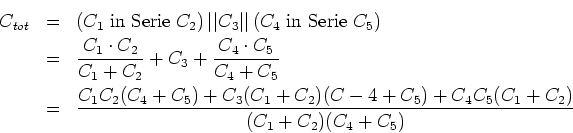
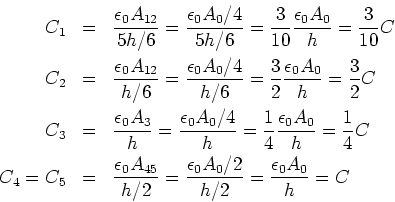
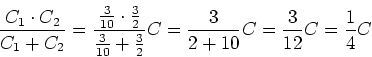
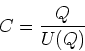
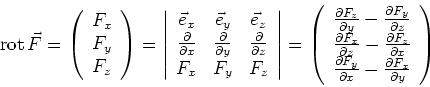
![\begin{eqnarray*}\textrm{rot} {}\vec F& =& \textrm{rot} {}\left(
\begin{array...
...rtial
r}\left(r \cdot F_\phi\right)\right)\right]\vec e_\theta
\end{eqnarray*}](img36.gif)
![\begin{eqnarray*}
\textrm{rot} {}\vec F_1(r,\phi,\theta) &=& \textrm{rot} {}\...
...l
r}\left(r\cdot 0\right)\right)\right]\vec e_\theta\\
&=& 0
\end{eqnarray*}](img37.gif)
![\begin{eqnarray*}
\textrm{rot} {}\vec F_2(r,\phi,\theta) &=& \textrm{rot} {}\...
...l
r}\left(r\cdot 0\right)\right)\right]\vec e_\theta\\
&=& 0
\end{eqnarray*}](img38.gif)
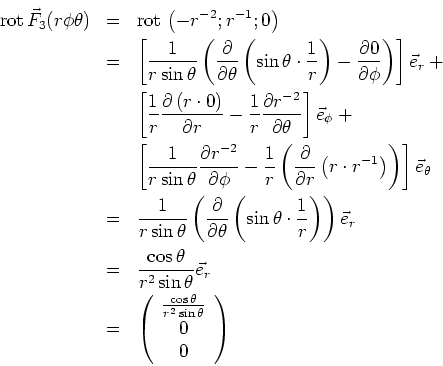
![\begin{eqnarray*}
\textrm{rot} {}\vec F_4(x,y,z) &=& \textrm{rot} {}\left(x-y...
...ght]\vec e_y\\
&&+
\left[ -1-(-1) \right]\vec
e_z\\
&=& 0
\end{eqnarray*}](img40.gif)