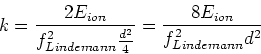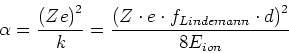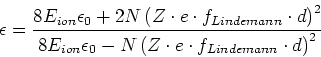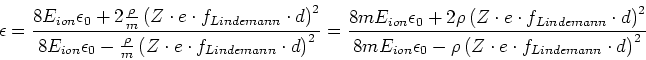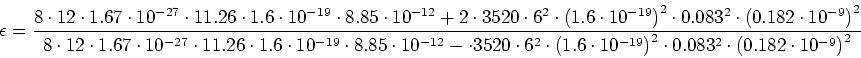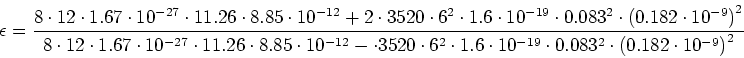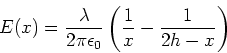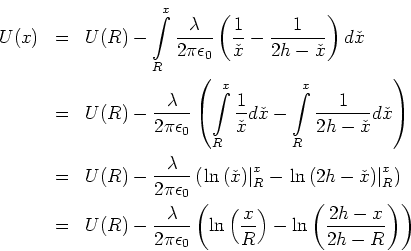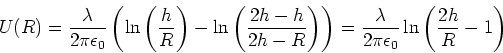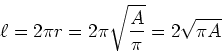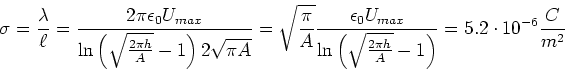

Up: PHYS3100 Grundkurs IIIb
Übungsblatt 04
PHYS3100 Grundkurs IIIb (Physik, Wirtschaftsphysik, Physik Lehramt)
Othmar Marti, (othmar.marti@physik.uni-ulm.de)
1. 12. 2003 oder 8. 12. 2003
- Mit Kondensatoren der Grösse
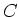 wird ein Würfel zusammengelötet. Wie gross ist die Ersatzkapazität
entlang der Raumdiagonale?
wird ein Würfel zusammengelötet. Wie gross ist die Ersatzkapazität
entlang der Raumdiagonale?
- Mit Kondensatoren der Grösse
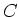 wird ein Rhomben-Dodekaeder zusammengelötet. Wie gross ist die Ersatzkapazität
entlang der Raumdiagonale zwischen gegenüberliegenden vierflächigen Ecken? Wie gross ist die Ersatzkapazität
entlang der Raumdiagonale zwischen gegenüberliegenden dreiflächigen Ecken?
wird ein Rhomben-Dodekaeder zusammengelötet. Wie gross ist die Ersatzkapazität
entlang der Raumdiagonale zwischen gegenüberliegenden vierflächigen Ecken? Wie gross ist die Ersatzkapazität
entlang der Raumdiagonale zwischen gegenüberliegenden dreiflächigen Ecken?
- Berechnen Sie die Dielektrizitätszahl für Kohlenstoff (
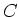 ). Bekannt ist:
). Bekannt ist: 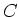 hat
eine Kernladungszahl
hat
eine Kernladungszahl 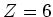 und eine Masse von
und eine Masse von 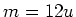 , wobei
, wobei
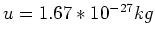 die atomare Masseneinheit
ist. Die Dichte ist
die atomare Masseneinheit
ist. Die Dichte ist 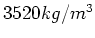 .
Ein
.
Ein 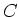 -Atom hat eine erste Ionisationsenergie von
-Atom hat eine erste Ionisationsenergie von
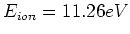 . Nehmen Sie ein klassisches
harmonisches Potential an und berechnen Sie die atomare Federkonstante
. Nehmen Sie ein klassisches
harmonisches Potential an und berechnen Sie die atomare Federkonstante 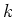 . Nach dem
Lindemann-Kriterium (u.a. der wissenschaftliche Berater von Winston Churchill) bricht eine Bindung auf
(quantenmechanisches Tunneln), wenn der
Bindungsabstand
. Nach dem
Lindemann-Kriterium (u.a. der wissenschaftliche Berater von Winston Churchill) bricht eine Bindung auf
(quantenmechanisches Tunneln), wenn der
Bindungsabstand
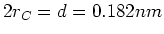 um
um 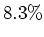 gedehnt wird. Vergleichen Sie das Resultat mit
gedehnt wird. Vergleichen Sie das Resultat mit
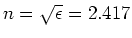 für Diamant.
für Diamant.
(Quelle: http://hyperphysics.phy-astr.gsu.edu/hbase/pertab/c.html#c1)
- Beim ersten Rastertunnelmikroskop (STM, erfunden von Binnig und Rohrer, Nobelpreis 1986) wurden
elektrostatische Klammern verwendet. Polierte Saphirplättchen (
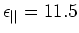 und
und
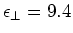 bezogen
auf die kristallographische
bezogen
auf die kristallographische 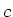 -Achse,
Quelle: http://bibliothek.fzk.de/zb/berichte/FZKA6496.pdf, Seite 29) mit einer Dicke
-Achse,
Quelle: http://bibliothek.fzk.de/zb/berichte/FZKA6496.pdf, Seite 29) mit einer Dicke 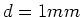 wurden zwischen einer
festen und einer beweglichen Elektrode angebracht. Zwischen den beiden Elektroden wurde eine Spannung von
wurden zwischen einer
festen und einer beweglichen Elektrode angebracht. Zwischen den beiden Elektroden wurde eine Spannung von
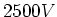 angelegt. Welche Haltekraft hatte diese Klammer, wenn die Elektroden Kreise mit
angelegt. Welche Haltekraft hatte diese Klammer, wenn die Elektroden Kreise mit 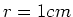 waren?
waren?
- Die Standbyschaltung eines Gerätes soll aus einem Kondensator mit
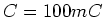 versorgt werden. Die
Ladespannung sei
versorgt werden. Die
Ladespannung sei 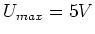 , die Endspannung, be der die Standbyschaltung nicht mehr arbeitet, sei
, die Endspannung, be der die Standbyschaltung nicht mehr arbeitet, sei
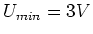 . Wie lange überbrückt die Standby-Schaltung einen Stromausfall, wenn ihr Verbrauch
. Wie lange überbrückt die Standby-Schaltung einen Stromausfall, wenn ihr Verbrauch 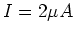 ist?
ist?
- Die Kugel oben bei einem van de Graaff-Generatoren hat einen Durchmesser von
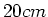 . Wie gross ist
die Oberflächenladungsdichte bei einer Spannung von
. Wie gross ist
die Oberflächenladungsdichte bei einer Spannung von 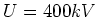 ?
?
- Wir modellieren den Fahrdraht der DB AG wie folgt: Ein zylinderförmiger Leiter, unendlich lang,
mit einer Querschnittsfläche von
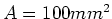 ist
ist 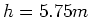 über einer unendlich ausgedehnten leitenden Ebene.
Die Spannung zwischen dem Fahrdraht und der Ebene ist sinusförmig, der RMS-Wert
über einer unendlich ausgedehnten leitenden Ebene.
Die Spannung zwischen dem Fahrdraht und der Ebene ist sinusförmig, der RMS-Wert
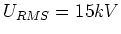 (
(
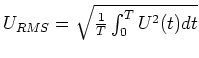 ). Wie gross ist die maximale Oberflächenladungsdichte
). Wie gross ist die maximale Oberflächenladungsdichte 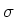 ,
gemittelt über den ganzen Umfang, auf dem
Fahrdraht?
,
gemittelt über den ganzen Umfang, auf dem
Fahrdraht?
- Die Situation sieht folgendermassen aus:
|
Die Raumdiagonale ist eine Symmetrieachse (3-zählige Rotationssymmetrie). Gesucht wird die
Ersatzkapazität zwischen A und D. Deshalb müssen die Spannungen an den Punkten 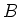 gleich sein, ebenso an
den Punkten gleich sein, ebenso an
den Punkten 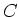 . .
Wir erhalten also folgende Ersatzschaltung:
|
|
|
Die Ersatzschaltung besteht also aus der Serieschaltung von drei Kondensatoren mit den Kapazitäten 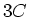 , ,
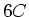 und und 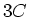
|
|
- Die Situation sieht folgendermassen aus:
|
|
|
Die Ersatzschaltung besteht also aus der Serieschaltung von vier Kondensatoren mit den Kapazitäten 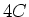 , ,
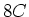 , , 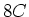 und und 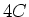
|
|
Die Situation sieht folgendermassen aus:
|
|
|
Die Ersatzschaltung besteht also aus der Serieschaltung von vier Kondensatoren mit den Kapazitäten 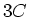 , ,
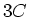 sowie der Parallelschaltung von je zwei Serieschaltungen von sowie der Parallelschaltung von je zwei Serieschaltungen von 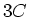 und und 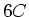 . .
|
|
- Die Ionisationsenergie ist
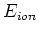
wobei 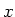 der Abstand ist, bei der die Ionisation eintritt. Wir haben auch
der Abstand ist, bei der die Ionisation eintritt. Wir haben auch
Nach Lindemann (
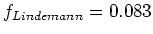 ) bricht (quantenmechanisches Tunneln)
eine Bindung, wenn Sie um
) bricht (quantenmechanisches Tunneln)
eine Bindung, wenn Sie um
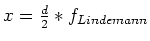 ausgelenkt wird (Auslenkung wird auf beide Atome aufgeteilt).
Also ist bei einer Bindungslänge
ausgelenkt wird (Auslenkung wird auf beide Atome aufgeteilt).
Also ist bei einer Bindungslänge 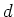
Die atomare Polarisierbarkeit ist also
Nach Clausius und Mosotti ist
Aufgelöst nach 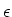
oder
Die Anzahl Atome errechnet sich aus
so dass wir
bekommen.
Eingesetzt (mit SI-Einheiten) erhalten wir
oder
oder
Zum Vergleich
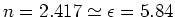 .
.
- Die potentielle Energie in einem Kondensator ist
Die Kapazität ist
Die Ladungsmenge auf dem Kondensator ist
Zusammen
Wenn der Abstand abnimmt, nimmt die potentielle Energie im Kondensator zu, sofern 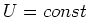 . Das heisst,
die Gesamtenergiebetrachtung muss die Batterie einschliessen. Sie liefert die Energie
. Das heisst,
die Gesamtenergiebetrachtung muss die Batterie einschliessen. Sie liefert die Energie
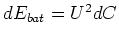 . Weiter
ist die mechanische Energie
. Weiter
ist die mechanische Energie 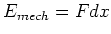 .
Wir erhalten also
.
Wir erhalten also
oder
Die Kraft ist
oder (mit
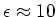 )
)
- Bei der Spannung
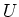 speichert ein Kondensator
speichert ein Kondensator 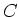 die Ladung
die Ladung
In unserem Falle kann die Ladungsmenge
als Strom fliessen. Mit
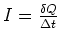 bekommen wir
bekommen wir
oder
- Die Kapazität ist
Dann ist die Ladung
Die Oberfläche ist
Also ist
Mit Zahlenwerten
- Das elektrische Feld um eine Linienladung ist (radial vom Leiter gesehen)
Das elektrische Feld auf der Verbindungslinie vom Draht zur Ebene ist die Überlagerung des Feldes mit seinem
Bildfeld.
Wir haben dann, wenn 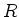 der Radius des Leiters ist,
der Radius des Leiters ist,
Wir setzen 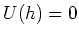 und erhalten
und erhalten
Der Umfang 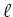 des Drahtes beträgt
des Drahtes beträgt
Die Flächenladungsdichte ist dann
Weiter ist die maximale Spannung
Zusammen
Übungsblatt 04
PHYS3100 Grundkurs IIIb (Physik, Wirtschaftsphysik, Physik Lehramt)
This document was generated using the
LaTeX2HTML translator Version 99.2beta8 (1.46)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html uebungsblatt04
The translation was initiated by marti on 2003-12-19


Up: PHYS3100 Grundkurs IIIb
Othmar Marti
Experimentelle Physik
Universiät Ulm
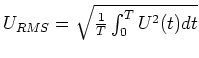 ). Wie gross ist die maximale Oberflächenladungsdichte
). Wie gross ist die maximale Oberflächenladungsdichte 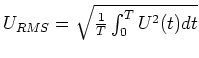 ). Wie gross ist die maximale Oberflächenladungsdichte
). Wie gross ist die maximale Oberflächenladungsdichte