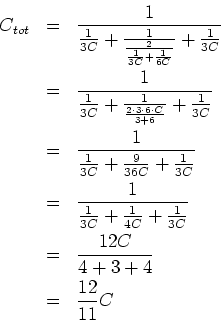

Up: PHYS3100 Grundkurs IIIb
Übungsblatt 05
PHYS3100 Grundkurs IIIb (Physik, Wirtschaftsphysik, Physik Lehramt)
Othmar Marti, (othmar.marti@physik.uni-ulm.de)
15. 12. 2003 oder 12. 1. 2004
- In einer Leitung, die parallel zur
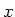 -Achse liegt, befindet sich flüssiges Natrium.
Entlang der
-Achse liegt, befindet sich flüssiges Natrium.
Entlang der 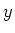 -Achse wird die magnetische Induktion
-Achse wird die magnetische Induktion 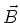 angelegt. Entlang der
angelegt. Entlang der 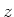 -Achse fliesst der
Strom
-Achse fliesst der
Strom 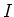 . Was soll die Anordnung bewirken?
. Was soll die Anordnung bewirken?
- Eine Wien-Robinson-Brücke sieht wie folgt aus:
![\includegraphics[width=0.3\textwidth]{ue-03-05-01.eps}](img6.gif)
Die Eingangsspannung ist 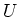 , die Ausgangsspannung ist
, die Ausgangsspannung ist 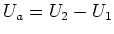 . Nehmen Sie an, dass
. Nehmen Sie an, dass
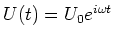 ist.
ist.
- Berechnen Sie
- Drücken Sie
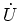 durch
durch 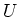 aus. Diese Funktion hat einen gemeinsamen, von
aus. Diese Funktion hat einen gemeinsamen, von 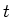 abhängigen Faktor.
Wird dieser abgespaltet, hängen die Vorfaktoren nur von
abhängigen Faktor.
Wird dieser abgespaltet, hängen die Vorfaktoren nur von
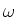 ab.
ab.
- Berechnen Sie für einen Kondensator das Äquivalent des Ohmschen Gesetzes
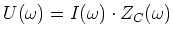 .
. 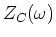 ist die komplexe Impedanz des Kondensators bei der Frequenz
ist die komplexe Impedanz des Kondensators bei der Frequenz
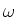 .
.
- Berechnen Sie für die Wien-Robinson-Brücke
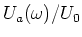 .
.
- Zur Definition: Eine leiterförmige Anordnung (Widerstandsleiter) besteht aus zwei Holmen, verbunden durch
Sprossen.
![\includegraphics[width=0.65\textwidth]{ue-03-05-02.eps}](img17.gif)
Die Enden des einen Holms heissen 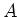 und
und 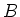 , die des anderen
, die des anderen 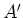 und
und 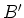 . - Man lötet eine sehr lange Leiter zusammen; jede Sprosse hat einen Widerstand
. - Man lötet eine sehr lange Leiter zusammen; jede Sprosse hat einen Widerstand
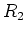 , jeder Holm hat zwischen je zwei Sprossen den Widerstand
, jeder Holm hat zwischen je zwei Sprossen den Widerstand 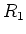 .
.
- Welchen Widerstand misst man zwischen den ''linken'' Enden
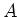 und
und 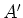 ?
?
- Wenn man an
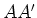 die
Spannung
die
Spannung 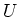 legt, welche Spannung misst man dann
legt, welche Spannung misst man dann
- zwischen den Lötstellen der
ersten Sprosse,
- der zweiten Sprosse,
- der
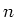 -ten Sprosse?
-ten Sprosse?
- Kann man z.B. erreichen, dass an jeder Sprosse genau halb soviel Spannung liegt wie an der
vorhergehenden?
- Wenn man gezwungen ist, die Leiter auf wenige Sprossen zu verkürzen: Was kann man tun, damit
sich der Widerstand zwischen
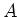 und
und 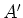 und die Spannungen an den verbleibenden Sprossen nicht
ändern? Hinweis: Wie ändert sich der Widerstand zwischen
und die Spannungen an den verbleibenden Sprossen nicht
ändern? Hinweis: Wie ändert sich der Widerstand zwischen 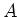 und
und 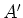 , wenn
Sie die ohnehin schon sehr lange Leiter um eine weitere Sprosse (
, wenn
Sie die ohnehin schon sehr lange Leiter um eine weitere Sprosse (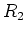 ) und
die beiden Holmstücke (
) und
die beiden Holmstücke (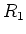 ) nach links verlängern?
) nach links verlängern?
- Der Large-Electron-Proton-Beschleuniger (LEP) des CERN hat einen Umfang von
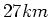 . Angenommen, das
Magnetfeld sei homogen entlang des Umfanges, wie gross müsste es sein um Elektronen mit dem Bruchteil
. Angenommen, das
Magnetfeld sei homogen entlang des Umfanges, wie gross müsste es sein um Elektronen mit dem Bruchteil
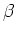 der Lichtgeschwindigkeit auf der Bahn zu halten?
der Lichtgeschwindigkeit auf der Bahn zu halten?
- In Wirklichkeit gibt es am LEP
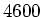 Magnete. Wie lang dürfen die Magnete maximal sein? Nehmen wir
Magnete. Wie lang dürfen die Magnete maximal sein? Nehmen wir
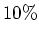 Füllung an, d.h. die Magnete beanspruchen eine totale Länge von
Füllung an, d.h. die Magnete beanspruchen eine totale Länge von 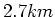 . Wie gross ist der Winkel
pro Magnet? Was ist der äquivalente Radius? Was wäre das maximale
. Wie gross ist der Winkel
pro Magnet? Was ist der äquivalente Radius? Was wäre das maximale 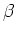 , wenn
, wenn 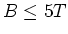 wäre?
wäre?
- Zwei unendlich ausgedehnte, parallele Kupferebenen mit der Dicke
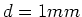 führen einen Gleichstrom von
führen einen Gleichstrom von 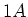 pro Breite
pro Breite 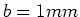 hin und
zurück. Die Spannung zwischen beiden Leitern beträgt
hin und
zurück. Die Spannung zwischen beiden Leitern beträgt 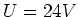 . Wie gross ist die relativistische Korrektur
des elektrischen Feldes zwischen den beiden Leitern?
. Wie gross ist die relativistische Korrektur
des elektrischen Feldes zwischen den beiden Leitern?
- Die Elektronen werden durch die Lorentz-Kraft in Richtung der Röhre abgelenkt. Da sie mit den
Natriumatomen stossen, übertragen sie einen Impuls in Richtung der Röhre und pumpen so das flüssige
Metall.
Siehe auch
Institut
für Geophysik Göttingen
- Wir erhalten
-
- Wir erhalten
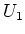 erhalten wir über
erhalten wir über
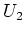 erhalten wir über
erhalten wir über
oder
also
Setzen wir 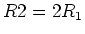 so ist
so ist
da
ist.
Zwischen 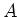 und
und 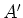 messe man den Widerstand
messe man den Widerstand 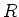 für eine sehr
lange Leiter.
für eine sehr
lange Leiter.
Aus der Tatsache, dass überhaupt etwas Endliches herauskommt, d. h. dass der Widerstand konvergiert, folgt,
dass man oben ein weiteres Glied anlöten kann, ohne 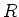 zu ändern.
zu ändern.
Die zu berechnende Schaltung ist:
![\includegraphics[width=0.45\textwidth]{ue-03-05-03.eps}](img51.gif)
Nur die Lösung mit 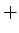 ist physikalisch sinnvoll, so dass wir
ist physikalisch sinnvoll, so dass wir
- Legen wir zwischen
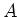 und
und 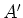 die Spannung
die Spannung 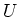 an, ist die Spannung über der ersten Sprosse
an, ist die Spannung über der ersten Sprosse
- Für die zweite Sprosse lautet die Gleichung:
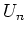 berechnet man, indem man diese Formel wiederholt anwendet. Wir benützen die Tatsache, dass der
Widerstand unserer unendlich langen Leiter konstant ist.
berechnet man, indem man diese Formel wiederholt anwendet. Wir benützen die Tatsache, dass der
Widerstand unserer unendlich langen Leiter konstant ist.
- Wir setzen
oder
Wir setzen
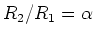 .
.
Also ist 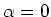 (unsinnig) oder
(unsinnig) oder
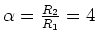
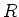 ist dann
ist dann 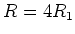 .
.
- Dieses
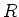 ist auch der Widerstand, mit dem man die kurze Leiter abschliessen muss, damit sie sich verhält
wie eine lange.
ist auch der Widerstand, mit dem man die kurze Leiter abschliessen muss, damit sie sich verhält
wie eine lange.
- Der Radius ist
Die Lorentzkraft ist gleich der durch der Geometrie bedingten Zentripetalkraft.
Die geschwindigkeitsabhängige Masse ist
also
Mit 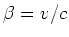 erhalten wir
erhalten wir
Zum Beispiel mit
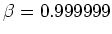 erhalten wir
erhalten wir 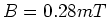
- Bei einer Länge von
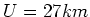 und 4600 Magneten stehen für jeden Magneten
und 4600 Magneten stehen für jeden Magneten
zur Verfügung. Der Füllfaktor von 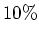 heisst, dass jeder Magnet
heisst, dass jeder Magnet
lang ist.
Zur Berechnung des Magnetfeldes kann angenommen werden, dass der Umfang nun
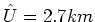 ist.
Aufgelöst erhalten wir
ist.
Aufgelöst erhalten wir
Eingesetzt erhalten wir (mit 20 signifikanten Stellen)
- Zur Berechnung verwenden wir, dass die elektrischen und magnetischen Felder unendlich ausgedehnter
Platten oder unendlich ausgedehnter homogener ebener Ströme unabhängig vom Abstand zur Platte oder zum
Strom sind.
Wir nehmen an, dass wir im Ruhezustand die Flächenladungsdichten 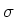 für die positiven wie für die
negativen Ladungen haben.
für die positiven wie für die
negativen Ladungen haben.
Das elektrische Feld einer homogen geladenen unendlich ausgedehnten Platte ist
Mit einer Rechnung analog zur Vorlesung (Kapitel 3.6.2) bekommt man
Das neue elektrische Feld ist also
Das elektrische Feld im Ruhesystem der bewegten Ladung ist dann (
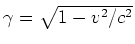 )
)
Die Kraft auf ein Teilchen im zweiten Leiter
Nun gilt für die Transformation der Kraft
Also ist
Im Querschnitt 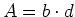 fliesst der Strom
fliesst der Strom 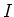 . Die Stromdichte ist
. Die Stromdichte ist 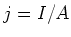 . Weiter ist
. Weiter ist
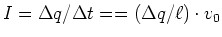 und damit
und damit
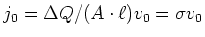 .
.
also ist
Mit
bekommen wir
und damit
Wir vergleichen diese Gleichung mit der Lorentzkraft 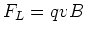 und können schreiben, dass die
relativistische Korrektur
und können schreiben, dass die
relativistische Korrektur
ist, wie auch anders in der Vorlesung abgeleitet.
Bemerkung: Die Angabe 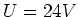 ist nicht notwendig.
ist nicht notwendig.
|
|
|
Die Ersatzschaltung besteht also aus der Serieschaltung von vier Kondensatoren mit den Kapazitäten 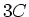 , ,
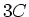 sowie der Parallelschaltung von je zwei Serieschaltungen von sowie der Parallelschaltung von je zwei Serieschaltungen von 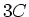 und und 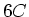 . .
|
|
Übungsblatt 05
PHYS3100 Grundkurs IIIb (Physik, Wirtschaftsphysik, Physik Lehramt)
This document was generated using the
LaTeX2HTML translator Version 99.2beta8 (1.46)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html uebungsblatt05
The translation was initiated by marti on 2004-01-13


Up: PHYS3100 Grundkurs IIIb
Othmar Marti
Experimentelle Physik
Universiät Ulm
![\includegraphics[width=0.3\textwidth]{ue-03-05-01.eps}](img6.gif)
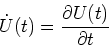
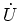 durch
durch 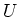 aus. Diese Funktion hat einen gemeinsamen, von
aus. Diese Funktion hat einen gemeinsamen, von 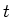 abhängigen Faktor.
Wird dieser abgespaltet, hängen die Vorfaktoren nur von
abhängigen Faktor.
Wird dieser abgespaltet, hängen die Vorfaktoren nur von
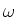 ab.
ab.
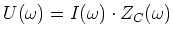 .
. 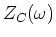 ist die komplexe Impedanz des Kondensators bei der Frequenz
ist die komplexe Impedanz des Kondensators bei der Frequenz
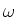 .
.
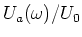 .
.
![\includegraphics[width=0.65\textwidth]{ue-03-05-02.eps}](img17.gif)
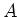 und
und 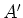 ?
?
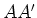 die
Spannung
die
Spannung 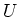 legt, welche Spannung misst man dann
legt, welche Spannung misst man dann
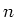 -ten Sprosse?
-ten Sprosse?
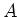 und
und 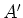 und die Spannungen an den verbleibenden Sprossen nicht
ändern? Hinweis: Wie ändert sich der Widerstand zwischen
und die Spannungen an den verbleibenden Sprossen nicht
ändern? Hinweis: Wie ändert sich der Widerstand zwischen 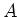 und
und 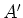 , wenn
Sie die ohnehin schon sehr lange Leiter um eine weitere Sprosse (
, wenn
Sie die ohnehin schon sehr lange Leiter um eine weitere Sprosse (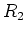 ) und
die beiden Holmstücke (
) und
die beiden Holmstücke (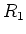 ) nach links verlängern?
) nach links verlängern?
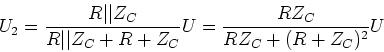
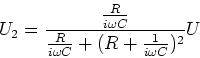
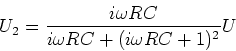
![\begin{displaymath}U_a = U_2-U_1 = \left[\frac{i\omega RC}{i\omega RC+(i\omega RC+1)^2}-\frac{R_2}{R_1+R_2}\right]U\end{displaymath}](img46.gif)
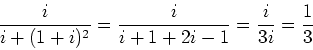
![\includegraphics[width=0.45\textwidth]{ue-03-05-03.eps}](img51.gif)
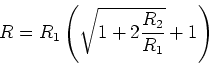
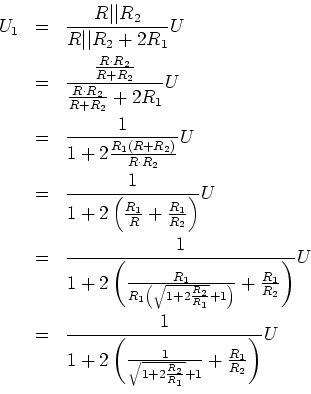
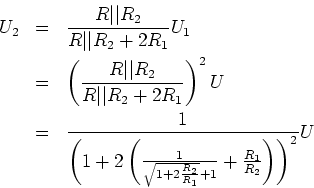
![\begin{displaymath}U_n = \frac{1}{\left[1+2\left(\frac{1}{\sqrt{1+2\frac{R_2}{R_1}}+1}+\frac{R_1}{R_2}\right)\right]^n}U\end{displaymath}](img63.gif)
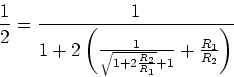
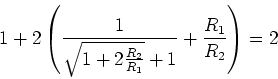
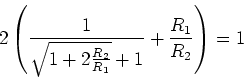
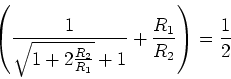
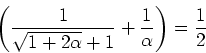
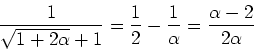
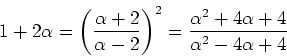
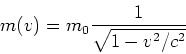
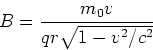
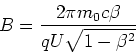
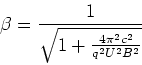
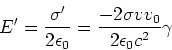
![\includegraphics[width=\textwidth]{ue-03-04-05.eps}](img115.gif)
![\includegraphics[width=0.8\textwidth]{ue-03-04-06.eps}](img120.gif)