

Up: PHYS3100 Grundkurs IIIb
Übungsblatt 06
PHYS3100 Grundkurs IIIb (Physik, Wirtschaftsphysik, Physik Lehramt)
Othmar Marti, (othmar.marti@physik.uni-ulm.de)
19. 1. 2004 oder 26. 1. 2004
- Die unten stehende Abbildung zeigt elf verschiedene Bahnkurven von Teilchen in einem homogenen
Magnetfeld, wie sie in einem teilchenphysikalischen Experiment gemessen werden können.
|
Abbildung aus Halliday, Resnick, Walker, Physik, Wiley Verlag, p. 833
|
Anders als bei der Teilchenphysik sind die Eigenschaften der Teilchen bekannt.
Die unten stehende Tabelle gibt die Masse, die Ladung und die Geschwindigkeiten an.
Ordnen Sie die Teilchenbahnen den Teilchen zu. Welche Bahn wäre in einer Nebelkammer nicht messbar?
- Der Stab in der Abbildung
![\includegraphics[width=0.7\textwidth]{ue-06-05.eps}](img2.gif)
habe den Widerstand 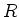 und der Widerstand der Schienen sowie die Kontaktwiderstände seien
vernachlässigbar. An die Punkte
und der Widerstand der Schienen sowie die Kontaktwiderstände seien
vernachlässigbar. An die Punkte 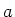 und
und 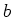 werde eine Spannungsquelle mit vernachlässigbarem
Innenwiderstand so angeschlossen, dass der Strom im Stab nach unten fliesst. Zum Zeitpunkt
werde eine Spannungsquelle mit vernachlässigbarem
Innenwiderstand so angeschlossen, dass der Strom im Stab nach unten fliesst. Zum Zeitpunkt 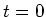 sei
der Stab in Ruhe.
sei
der Stab in Ruhe.
- Bestimmen Sie die Kraft auf den Stab als Funktion der Geschwindigkeit
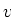 und formulieren Sie das
zweite Newtonsche Gesetz für den Stab, wenn er die Geschwindigkeit
und formulieren Sie das
zweite Newtonsche Gesetz für den Stab, wenn er die Geschwindigkeit 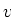 hat.
hat.
- Zeigen Sie, dass der Stab eine endliche Endgeschwindigkeit erreicht, und stellen sie für diese eine
Beziehung auf.
- Wie gross ist die Stromstärke, wenn der Stab seine Endgeschwindigkeit erreicht?
- In Elektromotoren schaltet man bisweilen einen Widerstand in Reihe zum Rotor, um den Anfangsstrom zu begrenzen, wenn
der Motor seine Nenndrehzahl noch nicht erreicht hat. Der Widerstand wird abgeschaltet, wenn der Motor
mit normaler Drehzahl läuft.
- Ein Motor habe den Widerstand
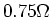 und nehme
und nehme 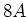 bei
bei 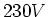 auf. Wie gross muss der
Zusatzwiderstand bemessen sein, damit der Anfangsstrom
auf. Wie gross muss der
Zusatzwiderstand bemessen sein, damit der Anfangsstrom 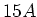 nicht überschreitet?
nicht überschreitet?
- Wie gross ist die Gegeninduktionsspannung, wenn der Motor seine Nenndrehzahl erreicht hat
und der Widerstand abgeschaltet ist?
- Es gibt die folgenden zwei Bauarten für Motoren:
![\includegraphics[width=0.95\textwidth]{ue-04-06-02.eps}](img12.gif)
Berechnen Sie für beide Motoren für ein Lastdrehmoment 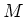 die resultierende Drehzahl
die resultierende Drehzahl 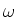 . Verwenden Sie
für die Spulen (Anker und Feldspulen) Konstanten, die alle nicht vom Strom abhängigen Grössen beinhalten.
Mitteln Sie weiter die Ströme und Drehmomente des Ankers über eine halbe Drehung. Nehmen Sie an, dass die
Feldspulen ein homogenes Magnetfeld erzeugen.
. Verwenden Sie
für die Spulen (Anker und Feldspulen) Konstanten, die alle nicht vom Strom abhängigen Grössen beinhalten.
Mitteln Sie weiter die Ströme und Drehmomente des Ankers über eine halbe Drehung. Nehmen Sie an, dass die
Feldspulen ein homogenes Magnetfeld erzeugen.
Zeichnen Sie 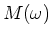 .
.
Welcher Motortyp würde sich bei fehlender Last und verschwindender Reibung zerstören?
Welcher Motortyp ist besser zur Beschleunigung aus dem Stand geeignet?
- Zeigen Sie mit Hilfe der Lorentztransformation der Felder, dass
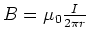 ist.
ist.
- Ein nichtleitender Zylinder der Masse
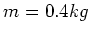 und der Länge
und der Länge 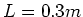 liegt auf einer schiefen Ebene.
liegt auf einer schiefen Ebene.
![\includegraphics[width=0.7\textwidth]{ue-04-06-03.eps}](img19.gif)
Auf den
Hohlzylinder ist, parallel zur Unterlage, eine Spule mit 20 Windungen so aufgewickelt, dass die Ebene der
Spule parallel zur schiefen Ebene ist. Wie gross muss der Strom in der Spule sein, damit der Zylinder in
einem Magnetfeld 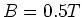 senkrecht zur Horizontalen gerade nicht rollt?
senkrecht zur Horizontalen gerade nicht rollt?
- In der gezeigten Stromschleife (Alle Leiter sind parallel zu den entsprechenden Koordinatenachsen!)
fliesst ein Strom von
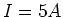 .
.
![\includegraphics[width=0.6\textwidth]{ue-04-06-04.eps}](img22.gif)
Bestimmen Sie den Betrag und die Richtung des magnetischen Momentes 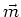 .
.
- Bahnen in Magnetfeldern werden durch
gegeben. Also ist
Im folgenden setzen wir 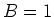 und beziehen alles auf die Grössen
und beziehen alles auf die Grössen 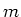 ,
, 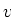 und
und 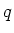 .
.
Aus der Zeichnung erhalten wir (inkl. Zuordnung)
-
- Wir berechnen zunächst den durch den Stab fliessenden Strom. Die Spannungsquelle
liefert eine Spannung
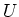 , und
der Stab induziert aufgrund seiner Bewegung eine Gegenspannung mit dem Betrag
, und
der Stab induziert aufgrund seiner Bewegung eine Gegenspannung mit dem Betrag 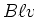 . Also ist die
resultierende Spannung
. Also ist die
resultierende Spannung 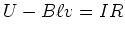 . Daraus folgt
. Daraus folgt
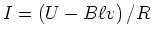 . Wegen dieses Stromes im Stab
wirkt auf ihn durch das magnetische Feld die Kraft
. Wegen dieses Stromes im Stab
wirkt auf ihn durch das magnetische Feld die Kraft
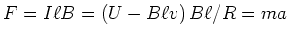 .
.
- Die Endgeschwindigkeit
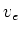 tritt auf, wenn
tritt auf, wenn 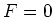 ist, also wenn gilt
ist, also wenn gilt
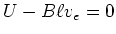 . Daraus folgt
. Daraus folgt
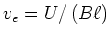 .
.
- Bei der Endgeschwindigkeit ist der Strom im Stab
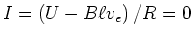 .
.
-
- Anfangs liegt keine Gegeninduktionsspannung vor, und der Strom ist
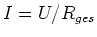 . Mit
. Mit 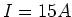 ist
ist
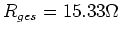 . Daher ist der Widerstand, der in Reihe zum Motor zu schalten ist,
. Daher ist der Widerstand, der in Reihe zum Motor zu schalten ist,
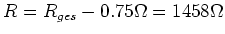 .
.
- Bei normaler Drehzahl ist der Spannungsabfall über dem Motor
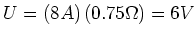 . Weil der Motor mit 230 V betrieben wird, entsteht eine Gegenspannung von 224 V.
. Weil der Motor mit 230 V betrieben wird, entsteht eine Gegenspannung von 224 V.
- Wir betrachten zuerst den Elektromotor als Generator. Der Fluss durch die Leiterschlaufe mit
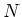 Windungen
und einer Fläche
Windungen
und einer Fläche 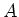 ist
ist
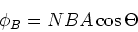 |
(1) |
wobei 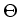 der Winkel zwischen der Normalen der Fläche der Leiterschlaufe und der Richtung des Magnetfeldes
ist. Mit
der Winkel zwischen der Normalen der Fläche der Leiterschlaufe und der Richtung des Magnetfeldes
ist. Mit
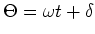 wird der zeitabhängige Fluss durch eine sich mit
wird der zeitabhängige Fluss durch eine sich mit 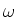 drehende
Leiterschlaufe
drehende
Leiterschlaufe
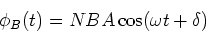 |
(2) |
Durch Ableiten erhält man die Induktionsspannung
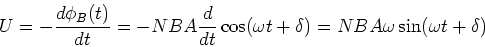 |
(3) |
Die induzierte effektive Spannung ist
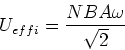 |
(4) |
- Wir betrachten den Nebenschlussmotor:
Wenn die Leiterschlaufe mit Spannung versorgt wird, arbeitet sie als Motor. Durch den Strom
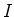 wird ein
Drehmoment
wird ein
Drehmoment
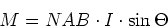 |
(5) |
erzeugt. Das mittlere Drehmoment bei einem Motor, bei dem der Kommutator immer bei dem Winkel, bei dem das
Drehmoment null wird, das Vorzeichen ändert, ist
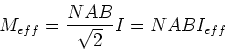 |
(6) |
Wenn der Widerstand des Ankers, der rotierenden Spule, 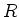 ist, kann man den mittleren Strom berechnen
ist, kann man den mittleren Strom berechnen
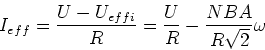 |
(7) |
Damit hängt das Drehmoment von der Drehzahl ab
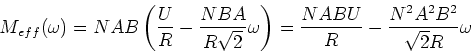 |
(8) |
Das Drehmoment des ruhenden Motors ist also
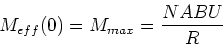 |
(9) |
und die maximale Drehzahl (da wo 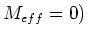 ist
ist
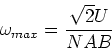 |
(10) |
Diese Charakteristik hat man immer dann, wenn das erregende Feld 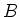 unabhängig von der Drehzahl ist, bei
Permanentmagneten oder wenn die Spule für die Erregerwicklung parallel zum Anker angeschlossen ist. Will man die
Drehzahl erhöhen, muss man das Feld
unabhängig von der Drehzahl ist, bei
Permanentmagneten oder wenn die Spule für die Erregerwicklung parallel zum Anker angeschlossen ist. Will man die
Drehzahl erhöhen, muss man das Feld 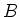 schwächer machen.
schwächer machen.
- Nun die Betrachtung für den Hauptschlussmotor:
Ist die Erregerwicklung in Serie zur Ankerwicklung geschaltet, gibt es keine maximale Drehzahl. Eine lange
Zylinderspule (Länge
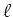 , Windungszahl
, Windungszahl 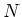 ) hat das Magnetfeld
) hat das Magnetfeld
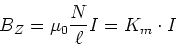 |
(11) |
Für andere Geometrien gilt das gleiche Gesetz, aber mit einem geometrieabhängigen Vorfaktor 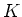 . Im statischen
Falle ist der Strom nur vom Gleichstromwiderstand
. Im statischen
Falle ist der Strom nur vom Gleichstromwiderstand 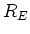 der Erregerspule abhängig. Wenn
der Erregerspule abhängig. Wenn 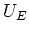 der Spannungsabfall
an der Erregerspule ist, ist
der Spannungsabfall
an der Erregerspule ist, ist
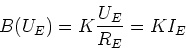 |
(12) |
Der durch den Anker fliessende Strom ist dann durch
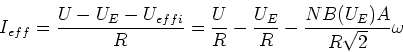 |
(13) |
gegeben. Wir erhalten
oder
und somit
Das resultierende Drehmoment ist
Das Drehmoment des ruhenden Motors ist
Es gibt kein maximales Drehmoment, da 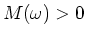 für alle
für alle 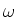 ist.
ist.
Dieser Motor wird durch Fliehkräfte zerrissen, wenn keine Reibung vorhanden ist.
![\includegraphics[width=0.7\textwidth]{ue-04-06-08.eps}](img74.gif)
- Nehmen wir an, die Linienladung
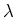 bewege sich in die
bewege sich in die 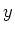 -Richtung mit der Geschwindigkeit
-Richtung mit der Geschwindigkeit 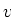 . Da
das Problem rotationssymmetrisch um die
. Da
das Problem rotationssymmetrisch um die 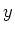 -Achse ist, betrachten wir nur Felder entlang der
-Achse ist, betrachten wir nur Felder entlang der
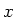 -Achse.
Das elektrische Feld der Linienladung auf der
-Achse.
Das elektrische Feld der Linienladung auf der 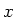 -Achse ist dann
-Achse ist dann
und
Wir verwenden
und damit
Nun ist 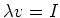 . Weiter ist in diesem Falle das Bezugssystem
. Weiter ist in diesem Falle das Bezugssystem 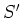 unser Laborsystem.
Weiter gilt, dass
unser Laborsystem.
Weiter gilt, dass
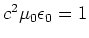 ist.
Wir haben also
ist.
Wir haben also
Unter der Annahme, dass 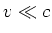 erhalten wir das klassische Resultat mit den richtigen
Vektororientierungen.
erhalten wir das klassische Resultat mit den richtigen
Vektororientierungen.
- Das Drehmoment eines magnetischen Momentes ist
Die Newtonschen Gesetze auf die Masse angewandt ergeben
wobei 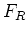 die Reibungskraft und
die Reibungskraft und 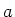 die Beschleunigung der Masse ist. Wenn der Zylinder den
Radius
die Beschleunigung der Masse ist. Wenn der Zylinder den
Radius 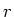 hat, ist das mechanische Drehmoment
hat, ist das mechanische Drehmoment 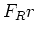 . Das magnetische Drehmoment ist
. Das magnetische Drehmoment ist
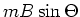 . Die Winkelbeschleunigung
. Die Winkelbeschleunigung 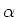 ist
ist
wobei 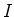 das Trägheitsmoment des Zylinders ist.
Im statischen Falle ist
das Trägheitsmoment des Zylinders ist.
Im statischen Falle ist 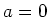 und
und 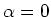 . Wir bekommen
. Wir bekommen
und
Das magnetische Moment einer Spule hängt von der Fläche 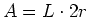 ab
ab
Also
oder
Also
- Wir teilen die Schlaufe in zwei Teile auf,
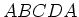 und
und 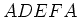 . Die Ströme sollen so sein, dass sie
sich auf der Strecke
. Die Ströme sollen so sein, dass sie
sich auf der Strecke 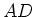 kompensieren. Wir haben also
kompensieren. Wir haben also
Wir setzen
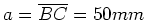 ,
,
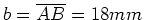 und
und
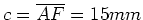 . Wir
bekommen
. Wir
bekommen
Die beiden Momente stehen senkrecht zueinander, also ist
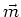 liegt in der
liegt in der 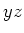 -Ebene.
-Ebene.
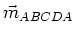 zeigt in die
zeigt in die 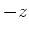 -Richtung,
-Richtung,
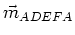 in die
in die
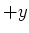 -Richtung. Der Winkel zur
-Richtung. Der Winkel zur 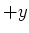 -Achse ist also
-Achse ist also
oder unter Berücksichtigung der Zweiwertigkeit des 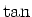
Übungsblatt 06
PHYS3100 Grundkurs IIIb (Physik, Wirtschaftsphysik, Physik Lehramt)
This document was generated using the
LaTeX2HTML translator Version 99.2beta8 (1.46)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html uebungsblatt06
The translation was initiated by marti on 2004-02-04


Up: PHYS3100 Grundkurs IIIb
Othmar Marti
Experimentelle Physik
Universiät Ulm
![\includegraphics[width=\textwidth]{ue-04-06-01.eps}](img1.gif)
![\includegraphics[width=0.7\textwidth]{ue-06-05.eps}](img2.gif)
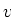 und formulieren Sie das
zweite Newtonsche Gesetz für den Stab, wenn er die Geschwindigkeit
und formulieren Sie das
zweite Newtonsche Gesetz für den Stab, wenn er die Geschwindigkeit 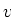 hat.
hat.
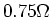 und nehme
und nehme 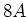 bei
bei 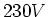 auf. Wie gross muss der
Zusatzwiderstand bemessen sein, damit der Anfangsstrom
auf. Wie gross muss der
Zusatzwiderstand bemessen sein, damit der Anfangsstrom 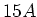 nicht überschreitet?
nicht überschreitet?
![\includegraphics[width=0.95\textwidth]{ue-04-06-02.eps}](img12.gif)
![\includegraphics[width=0.7\textwidth]{ue-04-06-03.eps}](img19.gif)
![\includegraphics[width=0.6\textwidth]{ue-04-06-04.eps}](img22.gif)
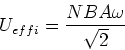
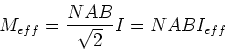
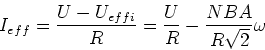
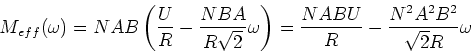
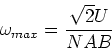
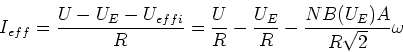
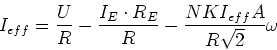
![\begin{displaymath}I_{eff}\left[1+\frac{NK A}{R\sqrt{2}}\omega+\frac{R_E}{R}\right] = \frac{U}{R}\end{displaymath}](img69.gif)
![\begin{displaymath}I_{eff} = \frac{U}{R\left[1+\frac{R_E}{R}+\frac{NK A}{R\sqrt{2}}\omega\right]}
=\frac{U}{R+R_E+\frac{NK A}{\sqrt{2}}\omega}\end{displaymath}](img70.gif)
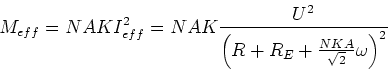
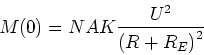
![\includegraphics[width=0.7\textwidth]{ue-04-06-08.eps}](img74.gif)