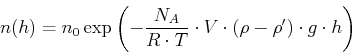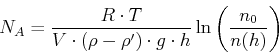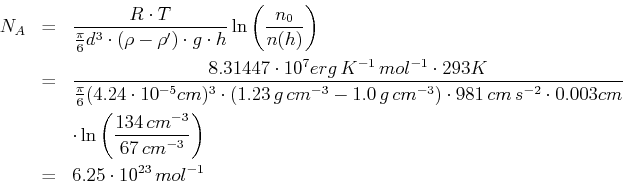

Up: PHYS4100 Grundkurs IV
Skript: PDF-Datei
Übungsblatt 01
PHYS4100 Grundkurs IV (Physik, Wirtschaftsphysik, Physik Lehramt)
Othmar Marti, (othmar.marti@uni-ulm.de)
14. 4. 2005 oder 15. 4. 2005
- Zirkon hat eine Molmasse von
 und eine Dichte von
und eine Dichte von
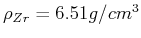 .
Berechne das Volumen eines
.
Berechne das Volumen eines 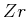 -Atoms.
-Atoms.
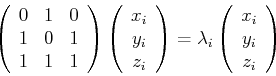
- Berechnen Sie die Eigenwerte der Matrix
- Zeigen Sie mit den Methoden der Wärmelehre, wie aus einem
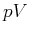 -Diagramm das Volumen eines Gasteilchens
bestimmt werden kann. Verwenden Sie dazu eine möglichst einfache Erweiterung des idealen Gasgesetzes.
-Diagramm das Volumen eines Gasteilchens
bestimmt werden kann. Verwenden Sie dazu eine möglichst einfache Erweiterung des idealen Gasgesetzes.
- Die folgende Abbildung aus ,,O. Marti, B. Drake, S. Gould and P.K. Hansma, Atomic Force Microscopy
and scanning tunneling microscopy with a combination atomic force microscope/scanning tunneling microscope, J.
Vacuum Sci. Technol A 6 (3), 2089-2092 (1988)``zeigt eine Graphitoberfläche mit Massstab.
|
Wie gross ist ein 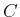 -Atom? Wie gross der Abstand zwischen nächsten Nachbarn? Was können Sie über
Bindungsverhältnisse aussagen? -Atom? Wie gross der Abstand zwischen nächsten Nachbarn? Was können Sie über
Bindungsverhältnisse aussagen?
|
|
- Kolloidteilchen werden in einer Flüssigkeit dispergiert.
- Zeigen Sie, dass die Teilchenzahldichte durch eine Boltzmann-Verteilung beschrieben wird
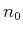 sei die Teilchenzahldichte in der Höhe
sei die Teilchenzahldichte in der Höhe 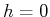 . Hinweis: Benützen Sie für die Herleitung von
. Hinweis: Benützen Sie für die Herleitung von
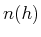 einen Ansatz analog zur barometrischen Höhenformel
einen Ansatz analog zur barometrischen Höhenformel
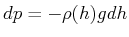 und vergessen Sie das
ideale Gasgesetz nicht.
und vergessen Sie das
ideale Gasgesetz nicht.
- Bestimmen Sie
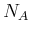 , wenn die experimentellen Daten wie folgt sind:
, wenn die experimentellen Daten wie folgt sind:
 ,
,
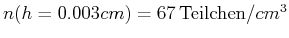 , die Dichte der Teilchen
, die Dichte der Teilchen
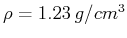 , die Dichte der
umgebenden Flüssigkeit
, die Dichte der
umgebenden Flüssigkeit
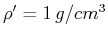 ,
, 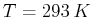 und der Teilchendurchmesser
und der Teilchendurchmesser
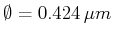 .
.
- Das Volumen eines
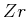 -Atoms ist
-Atoms ist
- Um die Eigenwerte von
zu berechnen löst man
Also muss man die folgende Gleichung lösen:
Dies Gleichung kann auch als
geschrieben werden.
Also ist
Die Eigenvektoren bestimmt man aus
Wir haben also die Gleichungssysteme
zu lösen. Die Lösungen sind
- Wir verwenden die van der Waals-Zustandsgleichung.
wobei 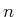 die Molzahl ist.
Das Co-Volumen
die Molzahl ist.
Das Co-Volumen 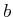 ist durch
ist durch
gegeben. Wenn 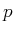 gross ist, sind die Abwichungen vom idealen
Gasgesetz durch
gross ist, sind die Abwichungen vom idealen
Gasgesetz durch 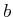 gegeben.
gegeben.
- Die Oberfläche hat die folgende Struktur:
Im STM-Bild sieht man Sechsecke. Der gemessene Abstand zwischen zwei
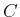 -Atomen ist
-Atomen ist
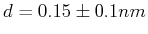 .
Dies muss etwa der Durchmesser eines
.
Dies muss etwa der Durchmesser eines 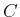 -Atoms sein. Fehler können zum Beispiel dadurch entstehen, dass
man die Effekte von Bindungen nicht berücksichtigt.
-Atoms sein. Fehler können zum Beispiel dadurch entstehen, dass
man die Effekte von Bindungen nicht berücksichtigt.
- Wir beginnen mit
Aus 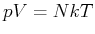 mit
mit 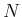 der Anzahl Teilchen bekommt man
der Anzahl Teilchen bekommt man
oder
mit 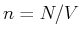 Damit ist
Damit ist
Weiter ist
wobei 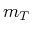 die Masse eines einzelnen Teilchens ist.
die Masse eines einzelnen Teilchens ist.
und
Hier haben wir nicht Gasteilchen, sondern Kugeln, wobei nur der Auftrieb wirksam ist. Also setzen wir
Die Lösung ist
- Wir lösen nach
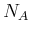 auf.
auf.
Das Volumen eines Teilchens mit dem Durchmesser 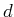 ist
ist
Also ist mit
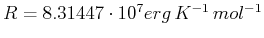


Up: PHYS4100 Grundkurs IV
Skript: PDF-Datei
Othmar Marti
Experimentelle Physik
Universiät Ulm
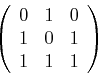
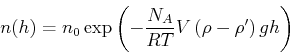
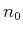 sei die Teilchenzahldichte in der Höhe
sei die Teilchenzahldichte in der Höhe 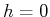 . Hinweis: Benützen Sie für die Herleitung von
. Hinweis: Benützen Sie für die Herleitung von
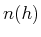 einen Ansatz analog zur barometrischen Höhenformel
einen Ansatz analog zur barometrischen Höhenformel
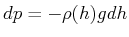 und vergessen Sie das
ideale Gasgesetz nicht.
und vergessen Sie das
ideale Gasgesetz nicht.
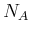 , wenn die experimentellen Daten wie folgt sind:
, wenn die experimentellen Daten wie folgt sind:
 ,
,
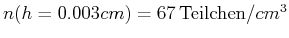 , die Dichte der Teilchen
, die Dichte der Teilchen
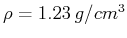 , die Dichte der
umgebenden Flüssigkeit
, die Dichte der
umgebenden Flüssigkeit
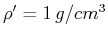 ,
, 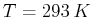 und der Teilchendurchmesser
und der Teilchendurchmesser
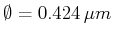 .
.
![\includegraphics[height=5cm]{graphit-stm.eps}](img6.gif)
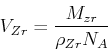
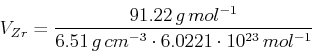
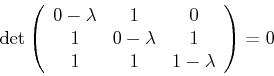
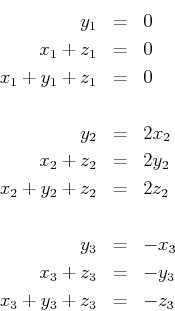
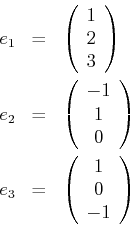
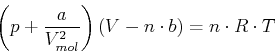
![\includegraphics[width=5cm]{graphit-modell.eps}](img35.gif)