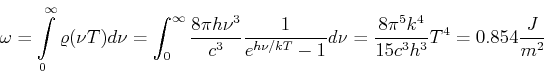

Up: PHYS4100 Grundkurs IV
Skript: PDF-Datei
Übungsblatt 02
PHYS4100 Grundkurs IV (Physik, Wirtschaftsphysik, Physik Lehramt)
Othmar Marti, (othmar.marti@uni-ulm.de)
21. 4. 2005 oder 22. 4. 2005
- Das Plancksche Strahlungsgesetz als Funktion der Frequenz
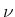 lautet:
lautet:
Geben Sie das Gesetz
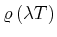 in Abhängigkeit von der
Wellenlänge
in Abhängigkeit von der
Wellenlänge 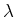 an.
an.
- Wie würde die Energieverteilung der schwarzen Strahlung aussehen, wenn es keine
erzwungene Emission gäbe?
Entspricht das einer bekannten Strahlungsformel?
Wie sieht man anschaulich, dass es nicht so sein kann?
- Berechnen Sie für beliebige
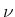 und
und 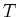 das Verhältnis der Wahrscheinlichkeit einer spontanen und
einer induzierten Emission. Skizzieren Sie den Verlauf von spontaner und induzierter Emission in Funktion
von
das Verhältnis der Wahrscheinlichkeit einer spontanen und
einer induzierten Emission. Skizzieren Sie den Verlauf von spontaner und induzierter Emission in Funktion
von 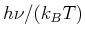 . Berechnen Sie die Frequenz, bei der spontane und induzierte Emission gleich
wahrscheinlich sind und skizzieren Sie den Verlauf für das Temperaturintervall
. Berechnen Sie die Frequenz, bei der spontane und induzierte Emission gleich
wahrscheinlich sind und skizzieren Sie den Verlauf für das Temperaturintervall
![$[1K\ldots 10000K]$](img7.gif) .
.
- Welche Temperatur hat eine schwarze Kugel von
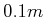 Durchmesser, die insgesamt
Durchmesser, die insgesamt 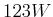 thermisch
abstrahlt?
Wie gross ist der Masseverlust pro Jahr?
thermisch
abstrahlt?
Wie gross ist der Masseverlust pro Jahr?
- Berechnen Sie die Temperatur der Sonne und die Energiedichte der Strahlung im Inneren unter der Annahme,
dass die Sonne ein sphärischer schwarzer Körper mit dem bekannten Sonnenradius ist. Die Intensität der
Strahlung auf der Erde ist
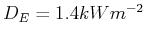 . Nehmen Sie zur Rechnung an, dass die Energiedichte im
Inneren homogen sei.
. Nehmen Sie zur Rechnung an, dass die Energiedichte im
Inneren homogen sei.
Ist das realistisch?
- Das Plancksche Gesetz lautet:
Um nach 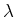 umzurechnen müssen wir
umzurechnen müssen wir
verwenden.
Dann gilt auch mit
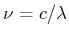
also bekommt man
- Ohne erzwungene Emission wäre die Einsteinsche Photonenbilanz anzusetzen:
Absorbierte Photonen/(cm3s) spontan emittierte Photonen/(cm3s)
Daraus folgt
Das ist das Wiensche Strahlungsgesetz. Es liefert maximale
Strahlungsdichte für die Frequenz 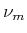 mit
mit
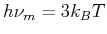 .
Das ist noch kein sehr grosser Unterschied
gegen das richtige Planck-Gesetz mit seinem Maximum bei
.
Das ist noch kein sehr grosser Unterschied
gegen das richtige Planck-Gesetz mit seinem Maximum bei
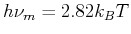 zwar würde das Wien-Gesetz eine
fast um 400° höhere Sonnentemperatur ergeben, aber wir wissen ja nicht a priori, wie heiss die Sonne
ist). Schlimmer wird es bei kleineren Frequenzen oder höheren Temperaturen: Bei
zwar würde das Wien-Gesetz eine
fast um 400° höhere Sonnentemperatur ergeben, aber wir wissen ja nicht a priori, wie heiss die Sonne
ist). Schlimmer wird es bei kleineren Frequenzen oder höheren Temperaturen: Bei
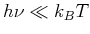 ergibt
Wien
ergibt
Wien
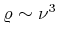 , Planck
, Planck
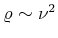 .
Ein 20 000 K-Strahler z. B. würde nach Wien im Sichtbaren kaum
.
Ein 20 000 K-Strahler z. B. würde nach Wien im Sichtbaren kaum 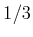 der Helligkeit
haben wie in Wirklichkeit.
der Helligkeit
haben wie in Wirklichkeit.
- Wir bezeichnen die Anzahl Prozesse pro Volumen und Zeit mit
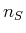 spontane Emission
spontane Emission
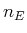 erzwungene Emission
erzwungene Emission
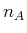 Absorption S
Absorption S
Strahlungsgleichgewicht:
Wir haben weiter für die Anzahl der angeregten Atome 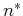 und die Anzahl der Grundzustandsatome
und die Anzahl der Grundzustandsatome 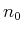 nach Boltzmann
nach Boltzmann
Aus der Vorlesung folgt mit den Einstein-Koeffizienten
Wir wollen 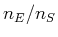 , das Verhältnis zwischen stimulierter und spontaner Emission berechnen
, das Verhältnis zwischen stimulierter und spontaner Emission berechnen
Die rechte Seite können wir aus einem Zwischenschritt der Ableitung des Planck-Gesetzes berechnen. Aus
bekommt man
Verwenden wir die reduzierte Variable 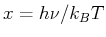 , so bekommen wir die Darstellung und berechnen
, so bekommen wir die Darstellung und berechnen
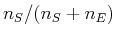 sowie
sowie 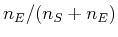
![\includegraphics[width=0.5\textwidth]{ue02-02.eps}](img42.gif)
Kleines 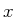 bedeutet kleine Frequenz, und bei kleinen Frequenzen ist die Emission vorwiegend stimuliert.
bedeutet kleine Frequenz, und bei kleinen Frequenzen ist die Emission vorwiegend stimuliert.
Der Übergang ist bei 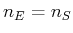 oder bei
oder bei
oder
oder
und damit die Grenze bei
![\includegraphics[width=0.5\textwidth]{ue02-04.eps}](img49.gif)
- Das Stefan-Boltzmann-Gesetz liefert
wobei 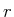 der Radius der Kugel und
der Radius der Kugel und 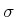 die Stefan-Boltzmann-Konstante ist.
die Stefan-Boltzmann-Konstante ist.
oder
Der Masseverlust ist
- Wir setzen den Sonnenradius
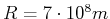 und den abstand Erde-Sonne
und den abstand Erde-Sonne
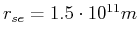 Der gesamte Strahlungsfluss von der Sonne ist konstant. Er beträgt
Der gesamte Strahlungsfluss von der Sonne ist konstant. Er beträgt
wobei 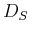 die Intensität der Strahlung auf der Sonnenoberfläche ist.
Aus Stefan-Boltzmann folgt
die Intensität der Strahlung auf der Sonnenoberfläche ist.
Aus Stefan-Boltzmann folgt
und
Durch die Integration der spektralen Energiedichte
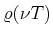 über die Frequenz ergibt die
Energiedichte.
über die Frequenz ergibt die
Energiedichte.
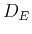 ist im Sonneninneren nicht konstant, da die Energie nicht punktförmig im Inneren erzeugt wird.
ist im Sonneninneren nicht konstant, da die Energie nicht punktförmig im Inneren erzeugt wird.


Up: PHYS4100 Grundkurs IV
Skript: PDF-Datei
Othmar Marti
Experimentelle Physik
Universiät Ulm
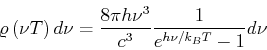
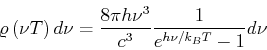
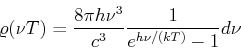
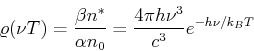
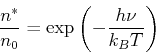
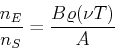
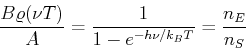
![\includegraphics[width=0.5\textwidth]{ue02-02.eps}](img42.gif)
![]() bedeutet kleine Frequenz, und bei kleinen Frequenzen ist die Emission vorwiegend stimuliert.
bedeutet kleine Frequenz, und bei kleinen Frequenzen ist die Emission vorwiegend stimuliert.
![]() oder bei
oder bei
![\includegraphics[width=0.5\textwidth]{ue02-04.eps}](img49.gif)
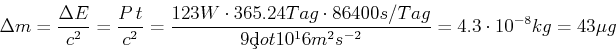
![\begin{displaymath}T = \sqrt[4]{\frac{D_S}{\sigma}}=\sqrt[4]{\frac{D_E r_{se}^2}{\sigma\cdot R^2}}= 5802 K\end{displaymath}](img62.gif)