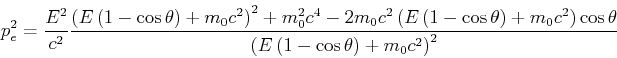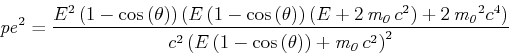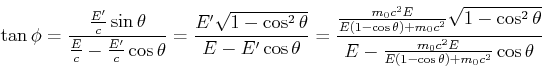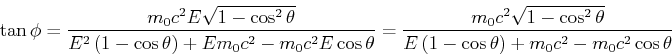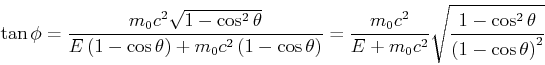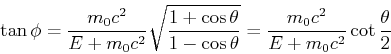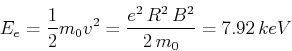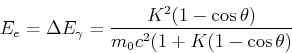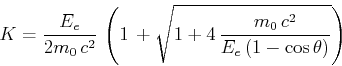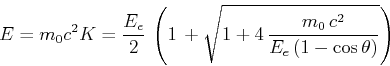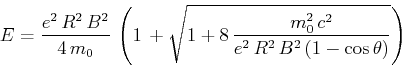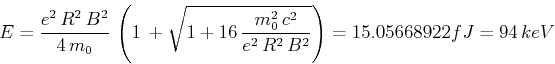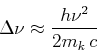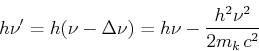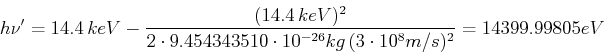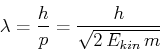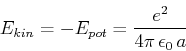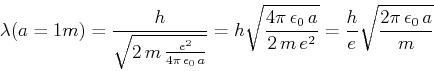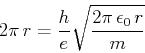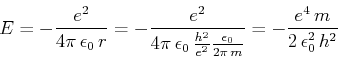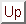

Up: PHYS4100 Grundkurs IV
Skript: PDF-Datei
Übungsblatt 03
PHYS4100 Grundkurs IV (Physik, Wirtschaftsphysik, Physik Lehramt)
Othmar Marti, (othmar.marti@uni-ulm.de)
28. 4. 2005 oder 29. 4. 2005
- Nehmen Sie an, dass eine Kugel mit dem Radius
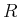 und der Masse
und der Masse 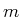 auf eine zweite
im Koordinatenursprung ruhende Kugel
mit dem gleichen Radius
auf eine zweite
im Koordinatenursprung ruhende Kugel
mit dem gleichen Radius 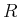 , aber einer Masse
, aber einer Masse 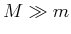 trifft. Der Stoss sei elastisch. Die anfängliche Geschwindigkeit der ersten Kugel sei
trifft. Der Stoss sei elastisch. Die anfängliche Geschwindigkeit der ersten Kugel sei 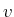 . Der Weg der
Kugel vor dem Aufprall sei parallel zu einer Gerade
. Der Weg der
Kugel vor dem Aufprall sei parallel zu einer Gerade 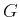 durch den Schwerpunkt der ruhenden Kugel.
durch den Schwerpunkt der ruhenden Kugel.
- Berechnen Sie den Streuwinkel
 als Funktion des Abstandes
als Funktion des Abstandes 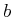 des des Weges der
ersten Kugel von der Gerade
des des Weges der
ersten Kugel von der Gerade 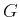 .
.
- Nehmen Sie an, dass
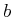 über den ganzen Wirkungsquerschnitt zufällig verteilt sei und
berechnen Sie die Winkelverteilung der gestreuten Kugeln.
über den ganzen Wirkungsquerschnitt zufällig verteilt sei und
berechnen Sie die Winkelverteilung der gestreuten Kugeln.
- Ein Photon der Energie
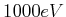 stösst mit einem freien, ruhenden
Elektron zusammen und wird um einen Winkel von
stösst mit einem freien, ruhenden
Elektron zusammen und wird um einen Winkel von 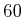 ° gestreut.
° gestreut.
- Wie ändern sich Frequenz, Energie und Wellenlänge des Photons?
- Wie gross ist die kinetische Energie, der Impuls und die Richtung des gestreuten Elektrons?
- Könnte dieses Elektron ein Metall mit der Austrittsarbeit
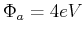 verlassen?
verlassen?
- Ein
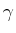 -Quant mit unbekannter Energie wird an einem Elektron durch den Compton-Effekt gestreut. Der
Streuwinkel
-Quant mit unbekannter Energie wird an einem Elektron durch den Compton-Effekt gestreut. Der
Streuwinkel 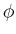 des Elektrons beträgt
des Elektrons beträgt 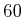 °. Das Rückstosselektron durchläuft nach dem Stoss eine
Kreisbahn mit
°. Das Rückstosselektron durchläuft nach dem Stoss eine
Kreisbahn mit 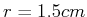 in einer magnetischen Induktion
in einer magnetischen Induktion 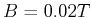 (senkrecht zur Bahnebene des
Elektrons). Welche Energie und Wellenlänge hatte das eintreffende
(senkrecht zur Bahnebene des
Elektrons). Welche Energie und Wellenlänge hatte das eintreffende 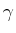 -Quant?
-Quant?
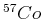 wandelt sich in
wandelt sich in 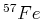 unter Aussendung eines Photons mit
unter Aussendung eines Photons mit
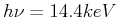 um. Berechnen
Sie die Energie des nicht rückstossfrei emittierten Photons. Wie gross ist die Geschwindigkeit des
um. Berechnen
Sie die Energie des nicht rückstossfrei emittierten Photons. Wie gross ist die Geschwindigkeit des
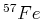 ?
?
- Ein Elektron befinde sich weit weg von einem Proton in Ruhe. Es wird vom Proton angezogen (warum?).
Berechnen Sie die de-Broglie-Wellenlänge für das ruhende Elektron, im Abstand von
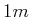 zum Proton und im
Abstand von
zum Proton und im
Abstand von
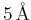 .
.
- Skizze des Stossprozesses:
![\includegraphics[width=0.8\linewidth]{ue03-03.eps}](img20.gif)
Nur die Komponente des Impulses senkrecht zur Kugeloberfläche wird umgeklappt (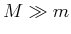 ).
).
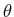 einsetzen
einsetzen
- Differentielle Grössen:
Wenn 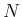 Kugeln eintreffen, ist die Anzahl gestreuter Kugeln (wie in der Vorlesung)
Kugeln eintreffen, ist die Anzahl gestreuter Kugeln (wie in der Vorlesung)
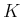 ist eine Normierungskonstante. Ohne Berücksichtigung der Vorzeichen erhalten wir
ist eine Normierungskonstante. Ohne Berücksichtigung der Vorzeichen erhalten wir
und
Aus
bekommt man
und
![\includegraphics[width=0.8\linewidth]{ue03-02.eps}](img35.gif)
-
- Skizze der Situation:
![\includegraphics[height=0.2\textheight]{ue03-01.eps}](img36.gif)
Erhaltungssätze: Energie (unter Vernachlässigung der Ruheenergie 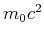 , d.h.
, d.h. 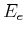 ist eine reine
kinetische Energie)
ist eine reine
kinetische Energie)
Impuls
und
aus der Relativitätstheorie: (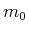 ist die Ruhemasse des Elektrons)
ist die Ruhemasse des Elektrons)
Mit
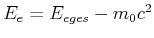 bekommt man
bekommt man
Wir addieren die Quadrate der Impulsbeziehungen und erhalten
und
Mit der Energie-Impuls-Beziehung bekommt man
oder
und
Also
Der Energieverlust des Photons ist
Eingesetzt (
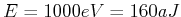 ,
,
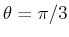 oder
oder
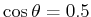 ,
,
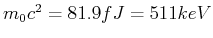 )
)
Frequenzänderung
Wellenlängenänderung
- Impulsaddition ergibt
Mit
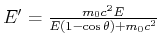 bekommt man
bekommt man
und
Eingesetzt:
Kinetische Enegie
Winkel: Wir dividieren die Impulsgesetze
und
- Nein
- Bahndaten:
Mit der Lösung aus der vorigen Aufgabe
mit
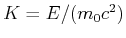 .
Aufgelöst:
.
Aufgelöst:
Aufgelöst
Mit
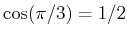
und
- Masse des
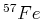 :
:
Vorlesung:
und damit
- nichtrelativistische Betrachtung
Im Abstand 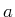 ist
ist
also
eingesetzt:
und
Die Wellenlänge ist gleich dem Bahnradius für
und
oder
Dies ist der klassische Abstand, bei dem gerade eine Wellenlänge auf einer Umlaufbahn Platz hat.
Die dazugehörige Bindungsenergie (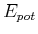 ist
ist
Diese Energie hat die richtige Grössenordnung, ist aber zu gross.
Wenn 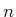 die Anzahl Wellen auf der Umlaufbahn ist, ist
die Anzahl Wellen auf der Umlaufbahn ist, ist
und
oder
Die dazugehörige Energie ist
Bemerkung: man bekommt das richtige Termschema!


Up: PHYS4100 Grundkurs IV
Skript: PDF-Datei
Othmar Marti
Experimentelle Physik
Universiät Ulm
 als Funktion des Abstandes
als Funktion des Abstandes 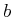 des des Weges der
ersten Kugel von der Gerade
des des Weges der
ersten Kugel von der Gerade 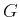 .
.
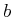 über den ganzen Wirkungsquerschnitt zufällig verteilt sei und
berechnen Sie die Winkelverteilung der gestreuten Kugeln.
über den ganzen Wirkungsquerschnitt zufällig verteilt sei und
berechnen Sie die Winkelverteilung der gestreuten Kugeln.
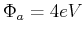 verlassen?
verlassen?
![\includegraphics[width=0.8\linewidth]{ue03-03.eps}](img20.gif)
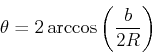
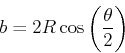
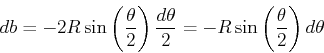
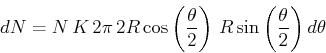
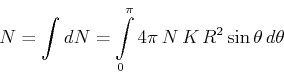
![\includegraphics[width=0.8\linewidth]{ue03-02.eps}](img35.gif)
![\includegraphics[height=0.2\textheight]{ue03-01.eps}](img36.gif)
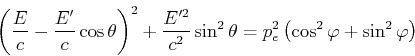
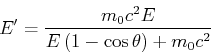
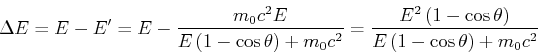
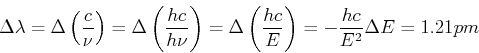
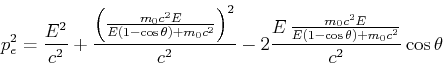
![\begin{displaymath}p_e^2 = \frac{E^2}{c^2}\left[1+ \left( \frac{m_0 c^2 }{E\left...
...{m_0 c^2 }{E\left(1-\cos\theta\right)+m_0c^2}\cos\theta\right] \end{displaymath}](img63.gif)
![\begin{displaymath}p_e^2 = \frac{E^2}{c^2}\left[1+ \frac{m_0^2 c^4 }{\left( E\le...
...( E\left(1-\cos\theta\right)+m_0c^2\right)^2}\cos\theta\right] \end{displaymath}](img64.gif)