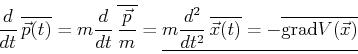

Up: PHYS4100 Grundkurs IV
Skript: PDF-Datei
Übungsblatt 04
PHYS4100 Grundkurs IV (Physik, Wirtschaftsphysik, Physik Lehramt)
Hans-Dieter Vollmer, (hans-dieter.vollmer@physik.uni-ulm.de)
12.5.2005 bzw. 13.5.2005
- Der Operator
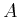 sei proportional zur Ableitung nach der Ortskoordinate,
d.h. es sei
sei proportional zur Ableitung nach der Ortskoordinate,
d.h. es sei
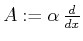 .
.
Wie muss die Konstante 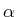 gewählt werden, damit
gewählt werden, damit 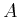 ein hermitescher
Operator ist?
ein hermitescher
Operator ist?
- Der Kommutator der Operatoren
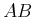 wird definiert durch
wird definiert durch
Zeigen Sie die folgenden Rechenregeln für Operatoren 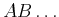 :
:
-
![$ [A,B] = - [B,A]$](img7.gif)
-
![$ [A,B+C] = [A,B] + [A,C]$](img8.gif)
-
![$ [AB,C] = A[B,C] + [A,C]B $](img9.gif)
-
![$ [A,BC] = [A,B]C + B[A,C] $](img10.gif)
- Berechnen Sie damit den Ausdruck
![$[AB,CD]$](img11.gif) .
.
- Berechnen Sie in der Ortsdarstellung den Kommutator von
Impulsoperator
 und Ortsoperator
und Ortsoperator 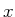 :
:
![$[p_x,x]$](img14.gif) .
.
- Ausgehend von dem Kommutator
![$ [x,p]= i\hbar$](img15.gif) soll gezeigt werden
(
soll gezeigt werden
(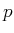 ist hier der Impulsoperator der
ist hier der Impulsoperator der 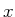 -Komponente):
-Komponente):
- Wenn
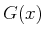 eine Funktion von
eine Funktion von 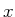 ist, die in eine
Taylorreihe an der Stelle
ist, die in eine
Taylorreihe an der Stelle 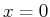 entwickelbar ist,
so gilt:
entwickelbar ist,
so gilt:
![$[p,G(x)] = -i\hbar\frac{dG(x)}{dx}$](img19.gif) .
.
- Wenn
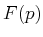 eine Funktion des Operators
eine Funktion des Operators 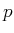 ist, die an der Stelle
ist, die an der Stelle 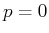 in eine
Taylorreihe entwickelbar ist,
dann gilt:
in eine
Taylorreihe entwickelbar ist,
dann gilt:
![$[x,F(p)] = i\hbar\frac{dF(p)}{dp}$](img22.gif) .
.
-
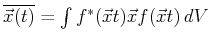 ist der zeitabhängige Mittelwert des Ortes eines Teilchens, dessen
Wellenfunktion
ist der zeitabhängige Mittelwert des Ortes eines Teilchens, dessen
Wellenfunktion 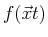 die quantenmechanische Bewegung beschreibt.
Das Teilchen bewege sich in einem Potential
die quantenmechanische Bewegung beschreibt.
Das Teilchen bewege sich in einem Potential 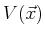 , so dass der
Hamiltonoperator durch
, so dass der
Hamiltonoperator durch
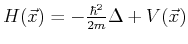 gegeben ist.
Berechnen Sie die Zeitableitung des Mittelwerts
gegeben ist.
Berechnen Sie die Zeitableitung des Mittelwerts
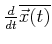 indem Sie benutzen, dass
indem Sie benutzen, dass 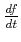 die zeitabhängige Schrödingergleichung erfüllen muss.
die zeitabhängige Schrödingergleichung erfüllen muss.
Leiten Sie so die folgende Differentialgleichung her:
- Berechnen Sie die Zeitableitung des Impulses in gleicher Weise wie in der
vorhergehenden Aufgabe und zeigen Sie damit die Bewegungsgleichung
Was ergibt sich durch Elimination des Impulsmittelwerts aus den beiden
Differentialgleichungen? Interpretieren Sie das Ergebnis.
- Die folgende Umformung eines Matrixelements
zeigt, dass die Bedingung für Hermitizität lautet:
Der Faktor muss also rein imaginär sein, wie dies beim
Impulsoperator auch der Fall ist.
-
-
-
-
-
-
Symbolisch also:
![$\displaystyle\left[\frac{\hbar}{i}\frac{d}{dx}, x \right] =\frac{\hbar}{i} $](img43.gif)
- Taylorreihe der Funktion
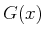 an der Stelle
an der Stelle 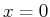 :
:
Damit folgt:
Somit:
- Taylorreihe des Operators
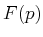 an der Stelle
an der Stelle 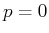 :
:
Damit folgt:
Somit:
- Der Mittelwert
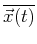 kann aus der Kenntnis
der zeitabhängigen Wellenfunktion berechnet werden,
die Lösung der zeitabhängigen Schrödingergleichung ist:
kann aus der Kenntnis
der zeitabhängigen Wellenfunktion berechnet werden,
die Lösung der zeitabhängigen Schrödingergleichung ist:
Dabei ist der Hamiltonoperator
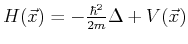 .
Er ist nicht von der Zeit abhängig!
.
Er ist nicht von der Zeit abhängig!
Damit gilt:
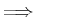
![\fbox{$\displaystyle
\frac{d}{dt}\,\overline{\vec{x}(t)}
= \frac{1}{i\hbar} \overline{[\vec{x},H]} $}](img56.gif)
Diese Gleichung besagt, dass die Ableitung des Mittelwerts gleich dem
Mittelwert des Kommutators
![$\frac{1}{i\hbar}[\vec{x},H]$](img57.gif) ist.
ist.
Wenn man die obige Rechnung genau betrachtet, stellt man fest, dass die
hier durchgeführten Umformungen nicht von 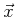 speziell
Gebrauch machen. Die Rechnung lässt sich deshalb z.B. auch für den
Impulsoperator so durchführen.
Der Kommutator ist:
speziell
Gebrauch machen. Die Rechnung lässt sich deshalb z.B. auch für den
Impulsoperator so durchführen.
Der Kommutator ist:
und damit
und schließlich
- Wir leiten wie oben her:
Dies ist das Newtonsche Grundgesetz für die Mittelwerte.
Durch Eliminiation des Impulsmittelwerts ergibt sich
also schließlich das Newtonsche Grundgesetz für die Mittelwerte
mit der äußeren Kraft
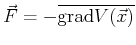 .
.
''Der Mittelwert des Orts bewegt sich nach nach dem Newtonschen
Grundgesetz''. Dies ist eine Formulierung des Ehrenfestschen Satzes.


Up: PHYS4100 Grundkurs IV
Skript: PDF-Datei
Othmar Marti
Experimentelle Physik
Universiät Ulm
![$ [A,B] = - [B,A]$](img7.gif)
![$ [A,B+C] = [A,B] + [A,C]$](img8.gif)
![$ [AB,C] = A[B,C] + [A,C]B $](img9.gif)
![$ [A,BC] = [A,B]C + B[A,C] $](img10.gif)
![$[AB,CD]$](img11.gif) .
.
 und Ortsoperator
und Ortsoperator 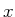 :
:
![$[p_x,x]$](img14.gif) .
.
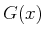 eine Funktion von
eine Funktion von 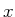 ist, die in eine
Taylorreihe an der Stelle
ist, die in eine
Taylorreihe an der Stelle 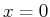 entwickelbar ist,
so gilt:
entwickelbar ist,
so gilt:
![$[p,G(x)] = -i\hbar\frac{dG(x)}{dx}$](img19.gif) .
.
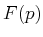 eine Funktion des Operators
eine Funktion des Operators 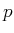 ist, die an der Stelle
ist, die an der Stelle 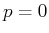 in eine
Taylorreihe entwickelbar ist,
dann gilt:
in eine
Taylorreihe entwickelbar ist,
dann gilt:
![$[x,F(p)] = i\hbar\frac{dF(p)}{dp}$](img22.gif) .
.
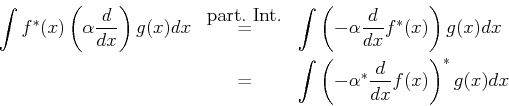
![\begin{displaymath}[AB,C]= ABC - CAB
= ABC - CAB + \underbrace{(ACB - ACB)}_0 \end{displaymath}](img37.gif)
![\begin{displaymath}[A,BC]= ABC - BCA
= ABC - BCA + \underbrace{(BAC - BAC)}_0 \end{displaymath}](img39.gif)
![\begin{eqnarray*}
\left[\frac{\hbar}{i}\frac{d}{dx}, x \right] f(x)
&=& \left(...
...{dx} f(x)
- x \frac{d}{dx} f(x)\right)
= \frac{\hbar}{i} f(x)
\end{eqnarray*}](img42.gif)
![$\displaystyle\left[\frac{\hbar}{i}\frac{d}{dx}, x \right] =\frac{\hbar}{i} $](img43.gif)
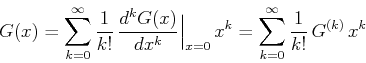
![\begin{displaymath}[p, G(x)]= \sum_{k=0}^{\infty}
\frac{1}{k!}\,G^{(k)} \,[p,x^k] \end{displaymath}](img45.gif)
![\begin{eqnarray*}[p,x^k]&=& [p,x] x^{k-1} + x [p,x] x^{k-2} + \ldots + x^{k-1}[p...
...(-i\hbar)
= -i\hbar\,k\, x^{k-1}
= -i\hbar\,\frac{d}{dx}\,x^k
\end{eqnarray*}](img46.gif)
![\begin{eqnarray*}[x, G(x)]
&=& \sum_{k=0}^{\infty} \frac{1}{k!}\,G^{(k)} \,[p,x...
...ty}\frac{1}{k!}\,G^{(k)} \,x^k
= - i\hbar\,\frac{d}{dx}\, G(x)
\end{eqnarray*}](img47.gif)
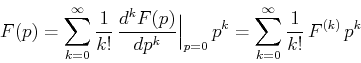
![\begin{displaymath}[x, F(p)]= \sum_{k=0}^{\infty}
\frac{1}{k!}\,F^{(k)} \,[x,p^k] \end{displaymath}](img49.gif)
![\begin{eqnarray*}[x,p^k]&=& [x,p] p^{k-1} + p [x,p] p^{k-2} + \ldots + p^{k-1}[x...
...-1}(i\hbar)
= i\hbar\,k\, p^{k-1}
= i\hbar\,\frac{d}{dp}\,p^k
\end{eqnarray*}](img50.gif)
![\begin{eqnarray*}[x, F(p)]
&=& \sum_{k=0}^{\infty} \frac{1}{k!}\,F^{(k)} \,[x,p...
...nfty}\frac{1}{k!}\,F^{(k)} \,p^k
= i\hbar\,\frac{d}{dp}\, F(p)
\end{eqnarray*}](img51.gif)
![\begin{eqnarray*}
\frac{d}{dt}\,\overline{\vec{x}(t)}
&=& \frac{d}{dt}\, \int ...
...int f^*(\vec{x},t)
\left[ \vec{x},H \right] f(\vec{x},t) dV\\
\end{eqnarray*}](img54.gif)
![\fbox{$\displaystyle
\frac{d}{dt}\,\overline{\vec{x}(t)}
= \frac{1}{i\hbar} \overline{[\vec{x},H]} $}](img56.gif)
![\begin{displaymath}[ \vec{x},H ]
= \left[\vec{x}\ ,\ \frac{\vec{p}^{\,2}}{2m} +...
...right]
= \frac{1}{2m} \left[\vec{x}\ ,\ \vec{p}^{\,2} \right] \end{displaymath}](img59.gif)
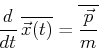
![\begin{displaymath}[ \vec{p},H ]
= \left[\vec{p}\ ,\ \frac{\vec{p}^{\,2}}{2m} + V(\vec{x})\right]
= \left[\vec{p}\ ,\ V(\vec{x}) \right] \end{displaymath}](img64.gif)