

Up: PHYS4100 Grundkurs IV
Skript: PDF-Datei
Übungsblatt 05
PHYS4100 Grundkurs IV (Physik, Wirtschaftsphysik, Physik Lehramt)
Hans-Dieter Vollmer, (hans-dieter.vollmer@physik.uni-ulm.de)
Date: 19.5.2005 bzw. 20.5.2005
- Ein Elektron bewege sich eindimensional in dem
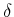 -förmigen Potential
-förmigen Potential
Ein solches Potential kann
man sich als hohes und schmales Rechteckpotential der Höhe 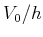 und der Breite
und der Breite 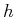 im
Grenzfall
im
Grenzfall
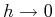 vorstellen.
vorstellen.
- Zeigen Sie, dass die zeitunabhängige Schrödingergleichung
für diese Bewegung auf die Differentialgleichung
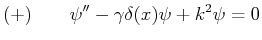
mit
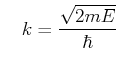
für die Wellenfunktion 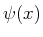 führt und bestimmen Sie den Faktor
führt und bestimmen Sie den Faktor 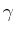 .
.
- Zeigen Sie, indem Sie die Differentialgleichung (+) von der
Stelle
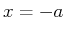 bis zur Stelle
bis zur Stelle 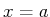 integrieren, dass sich im
Grenzwert
integrieren, dass sich im
Grenzwert
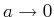 die sog. Sprungbedingung ergibt:
die sog. Sprungbedingung ergibt:
Sie bestimmt zusammen mit der Stetigkeitsbedingung
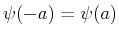 ,
wie die Wellenfunktionen links und rechts des Potentials miteinander
zusammenhängen.
,
wie die Wellenfunktionen links und rechts des Potentials miteinander
zusammenhängen.
- An dem Potential von Aufgabe 1. werde eine von links einfallende
Elektronenwelle mit dem Wellenvektor
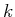 gestreut.
gestreut.
- Machen Sie einen für diese Situation geeigneten Ansatz jeweils
für die linke und rechte Seite des Potentials mit noch
unbekannten Amplituden.
Verknüpfen Sie die beiden Seiten, indem Sie die Sprung- und die
Stetigkeitsbedingung verwenden.
- Lösen Sie das lineare Gleichungssystem für die Amplituden.
Zeigen Sie so, dass die Amplitude der reflektierten Welle
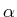 und die der durchgehenden Welle
und die der durchgehenden Welle 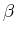 relativ zu der der einfallenden Welle bestimmt sind durch
relativ zu der der einfallenden Welle bestimmt sind durch
- Bestimmen Sie den Reflexionskoeffizienten
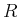 und den
Transmissionskoeffizienten
und den
Transmissionskoeffizienten 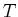 für die Rechnung von Aufgabe 2.
(Hinweis: Die beiden Koeffizienten sind gleich dem Betragsquadrat
der Amplitude der jeweiligen Welle, relativ zur einfallenden Welle.)
für die Rechnung von Aufgabe 2.
(Hinweis: Die beiden Koeffizienten sind gleich dem Betragsquadrat
der Amplitude der jeweiligen Welle, relativ zur einfallenden Welle.)
Zeigen Sie, dass für die obigen Lösungen 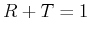 gilt.
gilt.
- Ein Elektron bewege sich frei in einem quaderförmigen Potentialtopf,
der unendlich hohe Potentialwände besitzt.
Die Kantenlängen seien
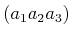 in
in 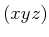 -Richtung.
-Richtung.
- Stellen Sie die zeitunabhängige Schrödingergleichung
für dieses Problem auf.
- Die partielle Differentialgleichung läßt sich durch
einen Separationsansatz
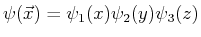 lösen.
Bestimmen Sie die Eigenwerte und Eigenfunktionen in jeder
der Raumrichtungen.
lösen.
Bestimmen Sie die Eigenwerte und Eigenfunktionen in jeder
der Raumrichtungen.
- Wie lauten Eigenwerte und Eigenfunktionen für den
quaderförmigen Hohlraum von Aufgabe 3?
- Betrachten Sie speziell einen Würfel mit Kantenlänge
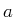 .
Wie sieht das Energiespektrum in diesem Fall aus und welche
Eigenfunktionen gehören jeweils zu den Energieeigenwerten?
.
Wie sieht das Energiespektrum in diesem Fall aus und welche
Eigenfunktionen gehören jeweils zu den Energieeigenwerten?
Welche Entartungen gibt es hier?
- Der Hamiltonoperator eines harmonischen Oszillators mit
Kreisfrequenz
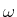 und Masse
und Masse 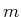 lautet
lautet
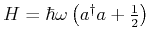 ,
wobei
,
wobei 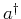 bzw.
bzw. 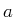 der Erzeugungs- bzw. der
Vernichtungsoperator ist.
Sie lauten in der Ortsdarstellung:
der Erzeugungs- bzw. der
Vernichtungsoperator ist.
Sie lauten in der Ortsdarstellung:
- Zeigen Sie für den Kommutator in der Ortsdarstellung:
![$[a,a^\dagger] = 1 $](img31.gif) .
.
- Die Wellenfunktion
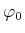 des Grundzustandes ist bestimmt
durch die Gleichung
des Grundzustandes ist bestimmt
durch die Gleichung
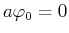 .
.
Stellen Sie diese Differentialgleichung
in der Ortsdartellung auf und integrieren Sie sie unter der
Bedingung, dass die Funktion
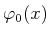 normiert sein muss.
Wie lautet somit die Eigenfunktion des Grundzustands in der
Ortsdarstellung explizit?
normiert sein muss.
Wie lautet somit die Eigenfunktion des Grundzustands in der
Ortsdarstellung explizit?
- Für den 1. angeregten Zustand gilt
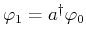 .
Berechnen Sie damit die Eigenfunktion
.
Berechnen Sie damit die Eigenfunktion
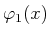 in
der Ortsdarstellung.
in
der Ortsdarstellung.
- Die zeitunabhängige Schrödingergleichung für die eindimensionale
Bewegung in einem Potential
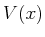 lautet:
lautet:
- Die Multiplikation mit
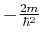 liefert:
Mit dem Potential
liefert:
Mit dem Potential
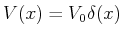 folgt:
folgt:
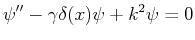
mit
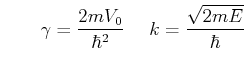
- Wir betrachten das Integral um das
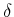 -Potential von
-Potential von 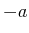 bis
bis
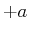 über die obige Differentialgleichung,
und gehen zum Limes
über die obige Differentialgleichung,
und gehen zum Limes
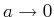 über. Dies ergibt:
da das dritte Integral dem Betrag nach
über. Dies ergibt:
da das dritte Integral dem Betrag nach
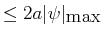 ist mit endlichem
ist mit endlichem
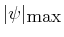 und daher
für
und daher
für
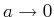 Null wird.
Damit folgt
Die Wellenfunktion ist an der Stelle der
Null wird.
Damit folgt
Die Wellenfunktion ist an der Stelle der 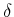 -Funktion
stetig und hat einen Knick (Sprung der Ableitung).
-Funktion
stetig und hat einen Knick (Sprung der Ableitung).
- Ansatz für die Wellenfunktion, wenn ein Elektronenstrahl
von links her einfällt.
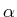 ist die Amplitude der
reflektierten Welle (prop.
ist die Amplitude der
reflektierten Welle (prop. 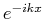 , läuft also nach
links),
, läuft also nach
links), 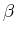 ist die Amplitude der durchgehenden Welle:
Stetigkeitsbedingung an der Stelle
ist die Amplitude der durchgehenden Welle:
Stetigkeitsbedingung an der Stelle 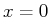 :
Sprungbedingung an der Stelle
:
Sprungbedingung an der Stelle 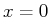 :
:
- Mit
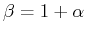 kann man
kann man 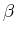 eliminieren und es folgt daraus
und somit
eliminieren und es folgt daraus
und somit
- Reflexionskoeffizient
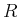 und Transmissionskoeffizient
und Transmissionskoeffizient 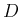 :
Offensichtlich gilt hier
:
Offensichtlich gilt hier 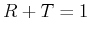 .
.
- Freie Bewegung in einem quaderförmigen Hohlraum
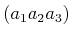 mit der Energie
mit der Energie 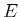 :
mit unendlich hohen Potentialwänden entsprechend den Randbedingungen
für die Schrödingergleichung:
:
mit unendlich hohen Potentialwänden entsprechend den Randbedingungen
für die Schrödingergleichung:
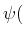 Rand
Rand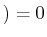 .
.
- Der Separationsansatz für die Wellenfunktion
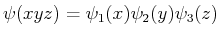 transformiert
die Schrödingergleichung in die Form
Für jede Raumrichtung
transformiert
die Schrödingergleichung in die Form
Für jede Raumrichtung 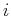 muss daher die Differentialgleichung
gelöst werden mit den Randbedingungen
muss daher die Differentialgleichung
gelöst werden mit den Randbedingungen
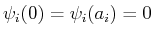 .
Die Lösungen der Differentialgleichung lauten
Diese Lösungen erfüllen bereits die Randbedingung
.
Die Lösungen der Differentialgleichung lauten
Diese Lösungen erfüllen bereits die Randbedingung
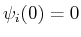 .
.
Die Randbedingung
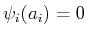 ist erfüllt, wenn gilt:
(der Eigenwert
ist erfüllt, wenn gilt:
(der Eigenwert 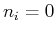 führt auf
führt auf 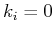 und damit auf die
triviale Eigenfunktion
und damit auf die
triviale Eigenfunktion 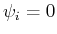 , die im übrigen
nicht normierbar ist).
, die im übrigen
nicht normierbar ist).
Damit sind auch die Energieeigenwerte festgelegt:
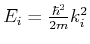 .
.
- Die Eigenwerte des Gesamtproblems sind somit
und die Eigenfunktionen
charakterisiert durch die Quantenzahlen
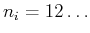 .
.
- Spezialfall Würfel:
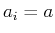 .
.
Die Eigenwerte des Gesamtproblems sind damit
und die Eigenfunktionen
Die Eigenfunktionen sind in der Regel entartet: Sie hängen
nur von
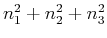 ab, nicht aber von den
individuellen
ab, nicht aber von den
individuellen 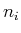 ;
eine Vertauschung der
;
eine Vertauschung der 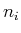 z.B. ändert die Energie nicht.
z.B. ändert die Energie nicht.
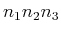 |
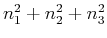 |
Entartung |
| 1 , 1 , 1 |
3 |
1 (Grundzustand) |
| 1 , 1 , 2 |
6 |
3 |
| 1 , 2 , 2 |
9 |
3 |
| 1 , 1 , 3 |
11 |
3 |
| 2 , 2 , 2 |
12 |
1 |
| 1 , 2 , 3 |
14 |
6 |
| 2 , 2 , 3 |
17 |
3 |
| 1 , 1 , 4 |
18 |
3 |
| 1 , 3 , 3 |
19 |
3 |
| 1 , 2 , 4 |
21 |
6 |
| 2 , 3 , 3 |
22 |
3 |
| 2 , 2 , 4 |
24 |
3 |
| 1 , 3 , 4 |
26 |
6 |
| 3 , 3 , 3 |
27 |
1 |
| 1 , 1 , 5 |
27 |
3 |
| 2 , 3 , 4 |
29 |
6 |
| 1 , 2 , 5 |
30 |
6 |
| 2 , 2 , 5 |
33 |
3 |
Die Eigenwerte sind 1-, 3- oder 6-fach entartet als Konsequenz
der Symmetrie in den 3 Raumrichtungen.
Einzelne mit
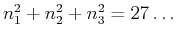 zeigen darüber hinaus
noch eine zufällige Entartung. zeigen darüber hinaus
noch eine zufällige Entartung.
|
- Die Erzeugungs- und Vernichtungsoperatoren lauten in der
Ortsdarstellung:
- Vertauschungsrelation:
- Grundzustand:
Der Grundstand ist der niedrigte Zustand: aus ihm kann man somit
durch Anwenden des Vernichtungsoperators keinen weiteren
Zustand erzeugen:
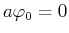 .
.
Diese Bedingung lautet in der Ortsdarstellung:
oder
Normierung:
Damit also
- 1. angeregter Zustand:
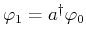
In der Ortsdarstellung lautet er:
Mit der Abkürzung
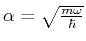 folgt:
folgt:


Up: PHYS4100 Grundkurs IV
Skript: PDF-Datei
Othmar Marti
Experimentelle Physik
Universiät Ulm
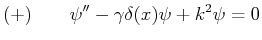 mit
mit 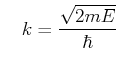
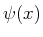 führt und bestimmen Sie den Faktor
führt und bestimmen Sie den Faktor 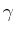 .
.
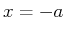 bis zur Stelle
bis zur Stelle 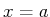 integrieren, dass sich im
Grenzwert
integrieren, dass sich im
Grenzwert
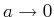 die sog. Sprungbedingung ergibt:
die sog. Sprungbedingung ergibt:
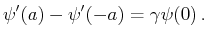
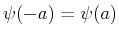 ,
wie die Wellenfunktionen links und rechts des Potentials miteinander
zusammenhängen.
,
wie die Wellenfunktionen links und rechts des Potentials miteinander
zusammenhängen.
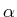 und die der durchgehenden Welle
und die der durchgehenden Welle 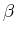 relativ zu der der einfallenden Welle bestimmt sind durch
relativ zu der der einfallenden Welle bestimmt sind durch 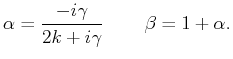
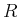 und den
Transmissionskoeffizienten
und den
Transmissionskoeffizienten 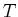 für die Rechnung von Aufgabe 2.
(Hinweis: Die beiden Koeffizienten sind gleich dem Betragsquadrat
der Amplitude der jeweiligen Welle, relativ zur einfallenden Welle.)
für die Rechnung von Aufgabe 2.
(Hinweis: Die beiden Koeffizienten sind gleich dem Betragsquadrat
der Amplitude der jeweiligen Welle, relativ zur einfallenden Welle.)
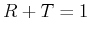 gilt.
gilt.
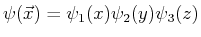 lösen.
Bestimmen Sie die Eigenwerte und Eigenfunktionen in jeder
der Raumrichtungen.
lösen.
Bestimmen Sie die Eigenwerte und Eigenfunktionen in jeder
der Raumrichtungen.
 .
Wie sieht das Energiespektrum in diesem Fall aus und welche
Eigenfunktionen gehören jeweils zu den Energieeigenwerten?
.
Wie sieht das Energiespektrum in diesem Fall aus und welche
Eigenfunktionen gehören jeweils zu den Energieeigenwerten?
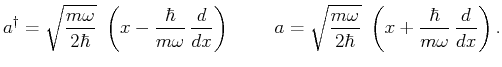
![$[a,a^\dagger] = 1 $](img31.gif) .
.
 des Grundzustandes ist bestimmt
durch die Gleichung
des Grundzustandes ist bestimmt
durch die Gleichung
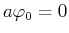 .
.
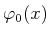 normiert sein muss.
Wie lautet somit die Eigenfunktion des Grundzustands in der
Ortsdarstellung explizit?
normiert sein muss.
Wie lautet somit die Eigenfunktion des Grundzustands in der
Ortsdarstellung explizit?
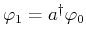 .
Berechnen Sie damit die Eigenfunktion
.
Berechnen Sie damit die Eigenfunktion
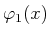 in
der Ortsdarstellung.
in
der Ortsdarstellung.
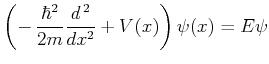
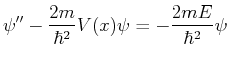
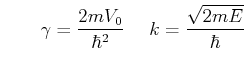
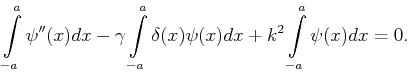
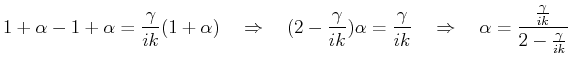
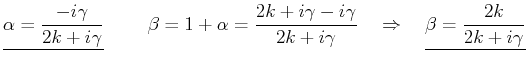
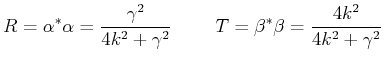
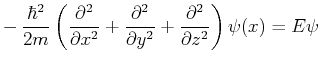
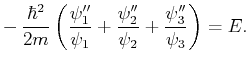
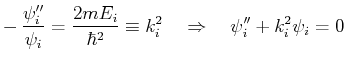
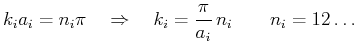
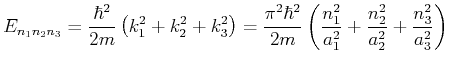
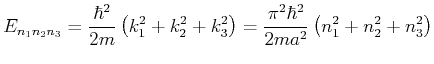
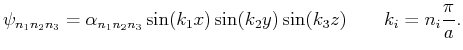
![$\displaystyle \left[\sqrt{\frac{m\omega}{2\hbar}}\
\left( x+\frac{\hbar}{m\ome...
...\omega}{2\hbar}}\
\left( x-\frac{\hbar}{m\omega}\, \frac{d}{dx}\right) \right]$](img93.gif)
![$\displaystyle \frac{m\omega}{2\hbar} \left[
\left( x+\frac{\hbar}{m\omega}\, \frac{d}{dx}\right),
\left( x-\frac{\hbar}{m\omega}\, \frac{d}{dx}\right) \right]$](img94.gif)
![$\displaystyle \frac{m\omega}{2\hbar}\frac{\hbar}{m\omega}
\left( - \left[x, \frac{d}{dx}\right]
+ \left[\frac{d}{dx} , x\right] \right)$](img95.gif)
![$\displaystyle \frac{1}{2} \left( - \left[x, \frac{d}{dx}\right]
+ \left[\frac{d...
...}{2} \left( \left[\frac{d}{dx},x\right]
+ \left[\frac{d}{dx} , x\right] \right)$](img96.gif)
![$\displaystyle \left[\frac{d}{dx},x\right] = 1$](img97.gif)
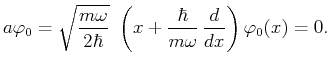
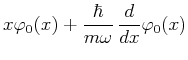
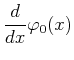
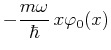
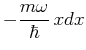
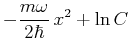
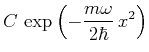
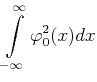
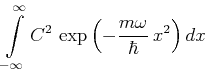
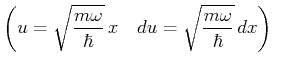
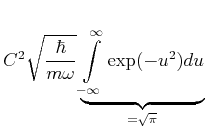
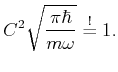
![$\displaystyle C = \sqrt[4]{\frac{m\omega}{\pi\hbar}}
\quad\Rightarrow\quad
\fbo...
...ac{m\omega}{\pi\hbar}}
\,\exp \left(-\frac{m\omega}{2\hbar} \, x^2\right)
$}\\ $](img114.gif)
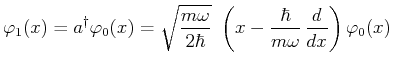
![$\displaystyle \frac{1}{\sqrt{2}} \left(\alpha x
- \frac{1}{\alpha} \frac{d}{dx} \right)
\frac{\sqrt{\alpha}}{\sqrt[4]{\pi}} \exp (- \alpha^2 x^2/2)$](img118.gif)
![$\displaystyle \frac{\sqrt{\alpha}}{\sqrt{2}\sqrt[4]{\pi}}
\left(\alpha x +\frac{1}{\alpha}\alpha^2 x \right)
\exp (- \alpha^2 x^2/2)$](img119.gif)
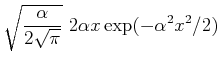
![$\displaystyle \sqrt{\frac{2}{\sqrt{\pi}}}\,
{\sqrt[4]{\frac{m\omega}{\hbar}}}^{\,3} x
\exp\left(-\frac{m\omega}{2\hbar}\, x^2\right)$](img121.gif)