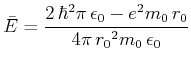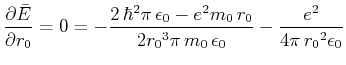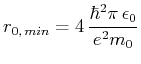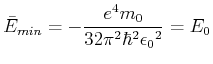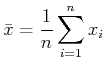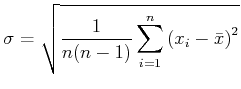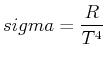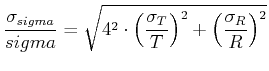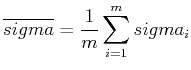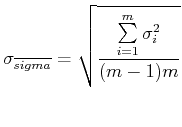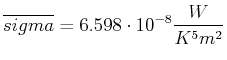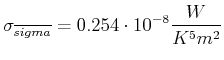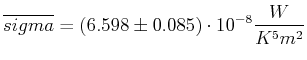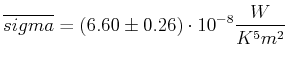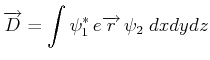
- Warum ist
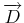 ein Vektor?
ein Vektor?
- Berechne die Komponenten von
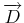 für
für
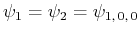 .
.
- Berechne die Komponenten von
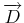 für
für
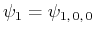 und
und
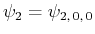 .
.
- Berechne die Komponenten von
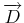 für
für
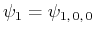 und
und
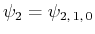 .
.
- Berechne die Komponenten von
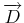 für
für
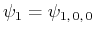 und
und
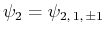 .
.
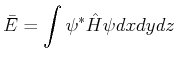
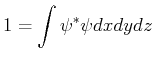
Berechnen Sie mit dem Variationsprinzip Wellenfunktionen und Energieeigenwerte des Wasserstoffatoms.
- Machen Sie den Ansatz
Bestimmen Sie die Normierungskonstante
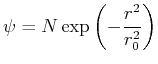
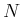 .
.
- Berechnen Sie
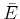 als Funktion von
als Funktion von 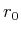 und minimieren Sie
und minimieren Sie 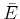 . Vergleichen Sie
dieses Minimum mit dem exakten Wert für den Energieeigenwert
. Vergleichen Sie
dieses Minimum mit dem exakten Wert für den Energieeigenwert 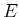 .
.
- Führen sie die gleiche Rechnung für den Ansatz
durch.
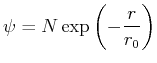
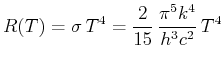
| Erste Messserie | Zweite Messerie | ||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
||||||||||||||||||||||||||||||||||||||||
| Dritte Messerie | |||||||||||||||||||||||||||||||||||||||||
|
Berechnen Sie den experimentellen Wert von
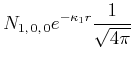
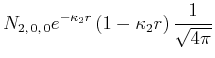
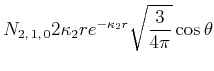
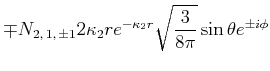
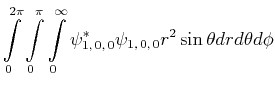
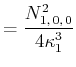
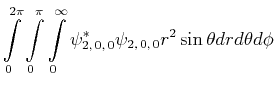
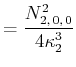
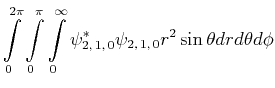
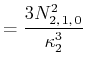
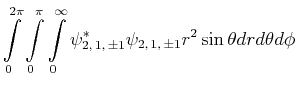
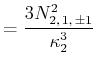
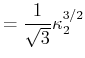
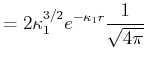
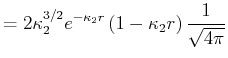
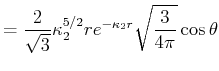
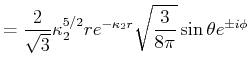
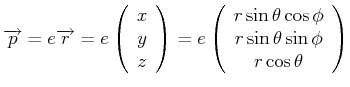
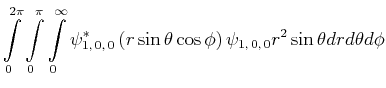
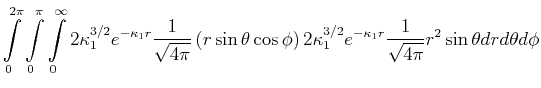
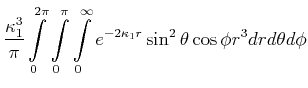
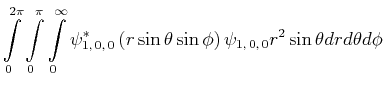
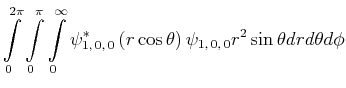
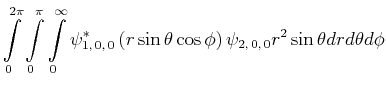
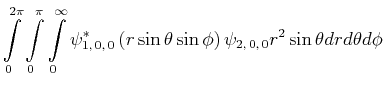
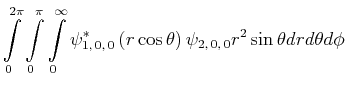
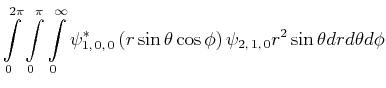
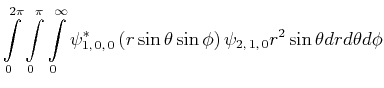
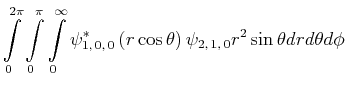
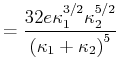
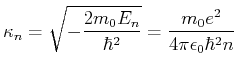
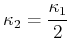
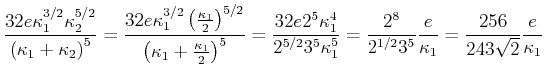
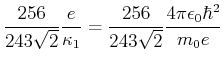
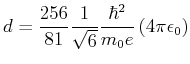
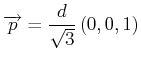
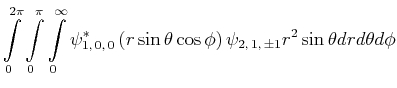
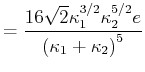
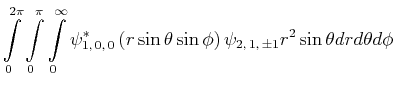
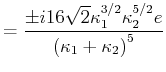
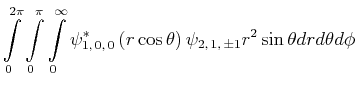
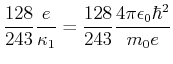
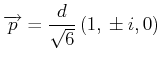
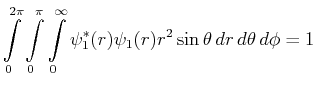
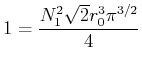
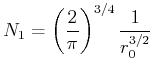
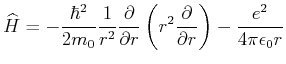
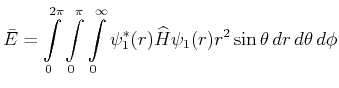
![$\displaystyle \bar{E} = \int\limits_0^{2\pi}\int\limits_0^\pi\int\limits_0^\inf...
...ac{e^2 \psi_1(r)}{4\pi\epsilon_0 r}\right]r^2 \sin\theta\, dr\, d\theta\,
d\phi$](img100.gif)
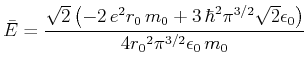
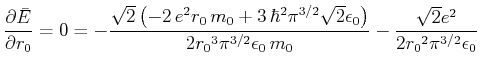
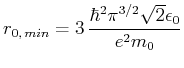
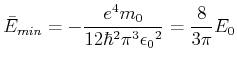
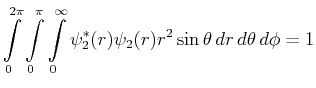
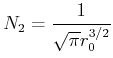
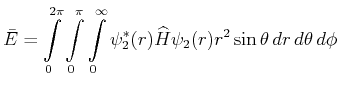
![$\displaystyle \bar{E} = \int\limits_0^{2\pi}\int\limits_0^\pi\int\limits_0^\inf...
...ac{e^2 \psi_2(r)}{4\pi\epsilon_0 r}\right]r^2 \sin\theta\, dr\, d\theta\,
d\phi$](img111.gif)