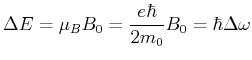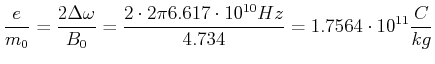

Up: PHYS4100 Grundkurs IV
Skript: PDF-Datei
Übungsblatt 08
PHYS4100 Grundkurs IV (Physik, Wirtschaftsphysik, Physik Lehramt)
Othmar Marti (othmar.marti@uni-ulm.de)
Date: 16. 6. 2005 oder 17. 6. 2005
- Die Spektrallinien, die den Übergang
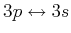 entsprechen, haben bei Natrium die
Wellenlängen
entsprechen, haben bei Natrium die
Wellenlängen
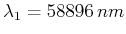 und
und
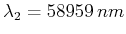 .
.
- Bestimmen Sie die Magnetfeldstärke, bei der das unterste Zeemann-Niveau des Terms
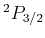 mit
dem obersten Niveau des Terms
mit
dem obersten Niveau des Terms 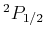 zusammenfallen würde, wenn die Bedingungen für den anomalen
Zeemanneffekt noch erfüllt wären.
zusammenfallen würde, wenn die Bedingungen für den anomalen
Zeemanneffekt noch erfüllt wären.
- Wie gross ist die Frequenzdifferenz zwischen den beiden äusseren Zeemann-Komponenten der
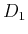 und
und
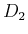 Linie in einem Magnetfeld der Stärke 1 Tesla?
Linie in einem Magnetfeld der Stärke 1 Tesla?
- Untersuchen Sie die Aufspaltung der Linien im
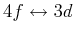 -Übergang bei Anwesenheit eines
Magnetfeldes, wenn die Zeemann-Aufspaltung verglichen mit der Spin-Bahn-Wechselwirkung schwach ist. Verwenden
Sie die Definition des Landéschen g-Faktors
-Übergang bei Anwesenheit eines
Magnetfeldes, wenn die Zeemann-Aufspaltung verglichen mit der Spin-Bahn-Wechselwirkung schwach ist. Verwenden
Sie die Definition des Landéschen g-Faktors
![$ g_j = 1+\left[j(j+1)+s(s+1)-l(l+1)\right]/\left[2j(j+1)\right]$](img9.gif)
- In einem Magnetfeld von
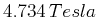 befinden sich Wasserstoffatome.
befinden sich Wasserstoffatome.
- Wird bei dieser Feldstärke die Aufspaltung der
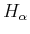 -Linie (
-Linie (
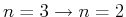 ) durch den
anomalen Zeemanneffekt oder durch den Paschen-Back-Effekt verursacht? Warum? (Die Spin-Bahn-Aufspaltung
zwischen den Termen
) durch den
anomalen Zeemanneffekt oder durch den Paschen-Back-Effekt verursacht? Warum? (Die Spin-Bahn-Aufspaltung
zwischen den Termen
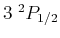 und
und
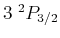 beträgt
beträgt
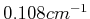 .
.
- Skizzieren Sie die Aufspaltung der Terme in dem angegebenen Magnetfeld und tragen Sie die Übergänge
ein, auf denen die
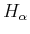 -Linie beobachtet werden kann.
-Linie beobachtet werden kann.
- In wieviele Komponenten spaltet die
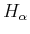 -Linie auf?
-Linie auf?
- Bestimmen Sie
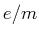 aus der beobachteten Frequenzaufspaltung zwischen zwei benachbarten Komponenten
von
aus der beobachteten Frequenzaufspaltung zwischen zwei benachbarten Komponenten
von
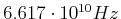 .
.
- Erwarten Sie für die erste Linie der Lyman-Serie (
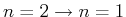 ) eine grössere, kleinere
oder gleiche Frequenzaufspaltung wie bei der
) eine grössere, kleinere
oder gleiche Frequenzaufspaltung wie bei der 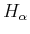 -Serie?
-Serie?
- Die Energiedifferenz zwischen den Zuständen
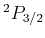 und
und
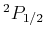 ohne Magnetfeld
Zusatzenergie im Magnetfeld
ohne Magnetfeld
Zusatzenergie im Magnetfeld
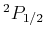 mit
mit 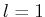 und
und 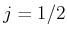 folgt
folgt 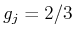 und
und
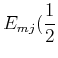
,
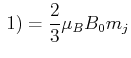
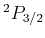 mit
mit 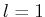 und
und 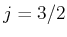 folgt
folgt 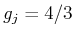 und
und
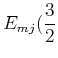
,
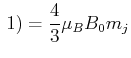
Das unterste Zeemann-Niveau von
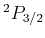 hat
hat 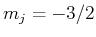 . Das oberste Zeemann-Niveau von
. Das oberste Zeemann-Niveau von
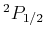 hat
hat 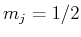 . Aus
folgt
. Aus
folgt
- Wenn der
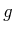 -Faktor des oberen Niveaus
-Faktor des oberen Niveaus
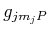 und der des unteren Niveaus
und der des unteren Niveaus
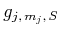 ist,
ist die maximale Differenz
Für die
ist,
ist die maximale Differenz
Für die 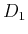 -Linie bekommt man
und
Für die
-Linie bekommt man
und
Für die 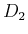 -Linie bekommt man
und
-Linie bekommt man
und
-
Wir haben
Auswahlregeln
- Wir berechnen
Die Spin-Bahn-Kopplungsenergie ist
Für den
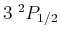 -Zustand ist
-Zustand ist
Für den
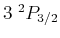 -Zustand ist
-Zustand ist
Die gesamte Aufspaltung durch die Spin-Bahn-Kopplung ist also
Wir vergleichen das mit der Zeemann-Aufspaltung
Für den
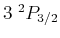 -Zustand ist
-Zustand ist
Für den
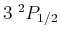 -Zustand ist
-Zustand ist
Wir nehmen den kleineren Wert und definieren die Grenze zwischen Zeemann-Effekt und Paschen-Back-Effekt
bei
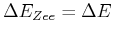 , also
, also
Wir sind im Regime des Paschen-Back-Effektes.
- Die Abweichung der Energie vom ungestörten Falle beim Paschen-Back-Effekt ist
Auswahlregeln:
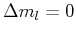
,
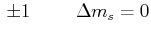
![\includegraphics[width=0.8\textwidth]{ue08-01.eps}](img153.gif)
Die Linien sind im Abstand
- Es gibt drei Linien.
- Der Abstand zwischen zwei Linien beim Paschen-Back-Effekt ist
und
- Die Niveau-Aufspaltung
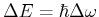 beim Paschen-Back-Effekt ist unabhängig
von der Hauptquantenzahl
beim Paschen-Back-Effekt ist unabhängig
von der Hauptquantenzahl 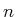 . Da die Lyman-Serie eine höhere Frequenz hat als die Balmer-Serie ist
. Da die Lyman-Serie eine höhere Frequenz hat als die Balmer-Serie ist


Up: PHYS4100 Grundkurs IV
Skript: PDF-Datei
Othmar Marti
Experimentelle Physik
Universiät Ulm
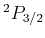 mit
dem obersten Niveau des Terms
mit
dem obersten Niveau des Terms 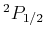 zusammenfallen würde, wenn die Bedingungen für den anomalen
Zeemanneffekt noch erfüllt wären.
zusammenfallen würde, wenn die Bedingungen für den anomalen
Zeemanneffekt noch erfüllt wären.
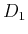 und
und
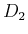 Linie in einem Magnetfeld der Stärke 1 Tesla?
Linie in einem Magnetfeld der Stärke 1 Tesla?
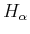 -Linie (
-Linie (
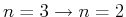 ) durch den
anomalen Zeemanneffekt oder durch den Paschen-Back-Effekt verursacht? Warum? (Die Spin-Bahn-Aufspaltung
zwischen den Termen
) durch den
anomalen Zeemanneffekt oder durch den Paschen-Back-Effekt verursacht? Warum? (Die Spin-Bahn-Aufspaltung
zwischen den Termen
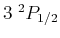 und
und
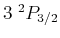 beträgt
beträgt
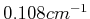 .
.
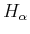 -Linie beobachtet werden kann.
-Linie beobachtet werden kann.
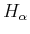 -Linie auf?
-Linie auf?
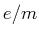 aus der beobachteten Frequenzaufspaltung zwischen zwei benachbarten Komponenten
von
aus der beobachteten Frequenzaufspaltung zwischen zwei benachbarten Komponenten
von
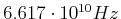 .
. 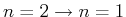 ) eine grössere, kleinere
oder gleiche Frequenzaufspaltung wie bei der
) eine grössere, kleinere
oder gleiche Frequenzaufspaltung wie bei der 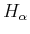 -Serie?
-Serie?
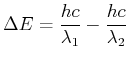
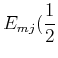 ,
,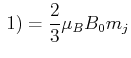
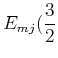 ,
,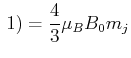
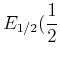 ,
,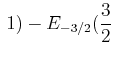 ,
,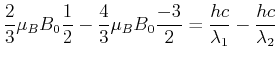
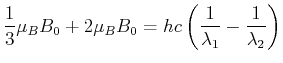
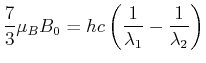
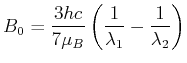
![$\displaystyle \Delta E_{D_1} =
\left[\left(\frac{1}{2}\frac{2}{3}+1\right)+\left(1+\frac{1}{2}\frac{2}{3}\right)\right]\mu_B B_0
= \frac{8}{3}\mu_B B_0$](img43.gif)
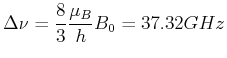
![$\displaystyle \Delta E_{D_2} =
\left[\left(\frac{1}{2}\frac{4}{3}+1\right)+\left(1+\frac{1}{2}\frac{4}{3}\right)\right]\mu_B B_0
= \frac{8}{3}\mu_B B_0$](img45.gif)
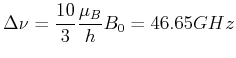
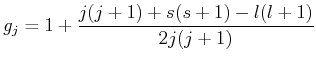
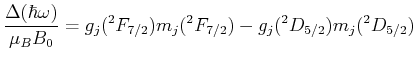
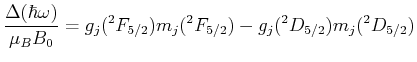
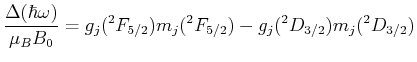
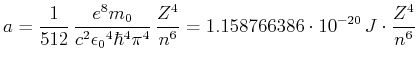
![$\displaystyle E_{l,s} = \frac{a}{2}\left[j(j+1)-l(l+1)-s(s+1)\right]$](img128.gif)
![$\displaystyle = \frac{1.158766386\cdot 10^{-20}\,J \cdot\frac{1^4}{3^6}}{2}\left[\frac{1}{2}\frac{3}{2}-1\cdot 2-\frac{1}{2}\frac{3}{2}\right]$](img131.gif)
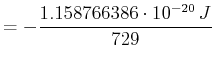
![$\displaystyle = \frac{1.158766386\cdot 10^{-20}\,J \cdot\frac{1^4}{3^6}}{2}\left[\frac{3}{2}\frac{5}{2}-1\cdot 2-\frac{1}{2}\frac{3}{2}\right]$](img135.gif)
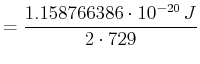
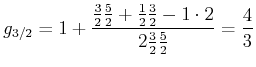
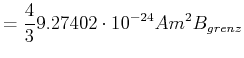
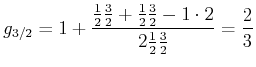
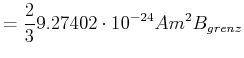
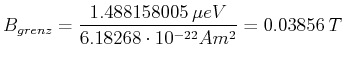
![\includegraphics[width=0.8\textwidth]{ue08-01.eps}](img153.gif)