next_inactive up previous
Up: PHYS4100 Grundkurs IV  Skript:  PDF-Datei

Übungsblatt 09
PHYS4100 Grundkurs IV (Physik, Wirtschaftsphysik, Physik Lehramt)

Othmar Marti, (othmar.marti@uni-ulm.de)


Date: 23. 6. 2005 oder 24. 6. 2005

Aufgaben

  1. Geben Sie für Helium bis zu den $ F$-Zuständen alle möglichen optischen Dipolübergänge an.
  2. Zeigen Sie, dass beim Wasserstoff-Atom der Störoperator beim quadratischen Stark-Effekt $ H^S_{\kappa\text{,} \kappa} =0$ ist.
  3. Nach einer pulsförmigen Anregung verschwindet die Amplitude eines Lichtfeldes wie

    $\displaystyle A(t) = A_0\left(e^{-\gamma t}e^{i\omega_0 t} + c.c.\right)$

    wobei $ c.c.$ konjugiert komplex bedeutet. Berechnen Sie mit der Fouriertransformation

    $\displaystyle \left\vert A(\omega)\right\vert^2$

    die Linienform. Wie gross ist die natürliche Linienbreite, wenn die Lebensdauer eines Niveaus $ 10 ns$ beträgt?
  4. Nehmen Sie an, die Geschwindigkeitsverteilung eines Gases sei durch die Maxwell-Boltzmann-Verteilung gegeben. Welche Linienform erwarten Sie nun? Wie gross ist die Linienbreite wenn $ T=500K$ ist?

Lösungen

  1. Die Auswahlregeln sind

    $\displaystyle \Delta l = \pm1 \hspace{1cm} \Delta m = 0$,$\displaystyle \,\pm 1$

    n 1 2 2 2 2 3 3 3 3 3 3 3 3 3
    l 0 0 1 1 1 0 1 1 1 2 2 2 2 2
    n l m 0 0 -1 0 1 0 -1 0 1 -2 -1 0 1 2
    1 0 0 $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$
    2 0 0 $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$
    2 1 -1 $ \sigma$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$
    2 1 0 $ \pi$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$
    2 1 1 $ \sigma$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$
    3 0 0 $ \sigma$ $ \pi$ $ \sigma$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$
    3 1 -1 $ \sigma$ $ \sigma$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$
    3 1 0 $ \pi$ $ \pi$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$
    3 1 1 $ \sigma$ $ \sigma$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$
    3 2 -2 $ \sigma$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$
    3 2 -1 $ \pi$ $ \sigma$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$
    3 2 0 $ \sigma$ $ \pi$ $ \sigma$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$
    3 2 1 $ \sigma$ $ \pi$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$
    3 2 2 $ \sigma$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$ $ \times$
    4 0 0 $ \sigma$ $ \pi$ $ \sigma$ $ \sigma$ $ \pi$ $ \sigma$
    4 1 -1 $ \sigma$ $ \sigma$ $ \sigma$ $ \sigma$ $ \pi$ $ \sigma$
    4 1 0 $ \pi$ $ \pi$ $ \pi$ $ \sigma$ $ \pi$ $ \sigma$
    4 1 1 $ \sigma$ $ \sigma$ $ \sigma$ $ \sigma$ $ \pi$ $ \sigma$
    4 2 -2 $ \sigma$ $ \sigma$
    4 2 -1 $ \pi$ $ \sigma$ $ \pi$ $ \sigma$
    4 2 0 $ \sigma$ $ \pi$ $ \sigma$ $ \sigma$ $ \pi$ $ \sigma$
    4 2 1 $ \sigma$ $ \pi$ $ \sigma$ $ \pi$
    4 2 2 $ \sigma$ $ \sigma$
    4 3 -3 $ \sigma$
    4 3 -2 $ \pi$ $ \sigma$
    4 3 -1 $ \sigma$ $ \pi$ $ \sigma$
    4 3 0 $ \sigma$ $ \pi$ $ \sigma$
    4 3 1 $ \sigma$ $ \pi$ $ \sigma$
    4 3 2 $ \sigma$ $ \pi$
    4 3 3 $ \sigma$
  2. Nach der Definition ist

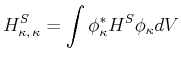
    $\displaystyle H_{\kappa\text{,}\,\kappa}^S= \int\phi_\kappa^* H^S \phi_\kappa dV$

    Nach den Auswahlregeln ist ein Übergang $ \kappa \rightarrow \kappa$ für Dipolübergänge verboten. Da der Störoperator sich aus dem Störpotential

    $\displaystyle V^S = e\vec{E}_{el} \vec{r}$

    ergibt, ist er proportional zu einem Dipolmoment $ e\vec{r}$. Aus dem Kapitel über Auswahlregeln folgt sofort die Behauptung.

  3. $\displaystyle A(t) = A_0 e^{-i\gamma t}\left(e^{i\omega_0 t}+e^{-i\omega t}\right)$

    Fouriertransformation:

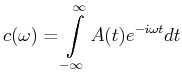
    $\displaystyle c(\omega) = \int\limits_{-\infty}^{\infty} A(t) e^{-i\omega t} dt$

    eingesetzt

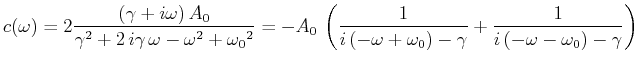
    $\displaystyle c(\omega) = 2{\frac { \left( {\gamma}+i{\omega} \right) {A_0}}{{{... ...gamma} }+ \frac{1}{ i \left( -{\omega}-{ \omega_0} \right) -{\gamma} } \right) $

    oder

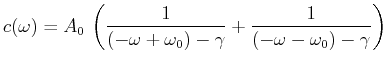
    $\displaystyle c(\omega) = {A_0}\, \left( \frac{1}{ \left( -{\omega}+{\omega_0} ... ...{\gamma} }+ \frac{1}{ \left( -{\omega}-{ \omega_0} \right) -{\gamma} } \right) $

    Der zweite Summand hat für $ \omega=0$ den Wert $ -1/(\omega_0+\gamma)$ und ist für alle Werte $ \omega>0$ betragsmässig kleiner. Der erste Summand hat ein Maximum bei $ \omega=\omega_0$. Wir vernachlässgen den zweiten Summanden und erhalten

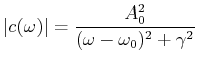
    $\displaystyle \left\vert c(\omega)\right\vert=\frac{A_0^2}{(\omega-\omega_0)^2+\gamma^2}$

    Wenn die Lebensdauer $ 10 ns$ ist, ist $ \gamma= 1/(2\tau)= 5\cdot 10^7\, Hz$.

  4. Die Maxwell-Boltzmann-Verteilung in die Richtung des $ k$-Vektors ist ($ v$ im Intervall $ [v,v+dv]$)

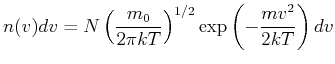
    $\displaystyle n(v)dv = N\left(\frac{m_0}{2\pi kT}\right)^{1/2} \exp\left(-\frac{m v^2}{2kT}\right)dv$

    wobei $ m$ die Masse des Atoms ist. Die Dopplerverschiebung ist

    $\displaystyle \omega = \omega_0(1\pm v/c)$

    oder

    $\displaystyle c(\omega-\omega_0)/\omega_0 = \pm v$

    Eingesetzt

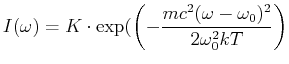
    $\displaystyle I(\omega)= K\cdot \exp(\left(-\frac{m c^2 (\omega-\omega_0)^2}{2\omega_0^2 k T}\right)$

    wobei $ K$ eine Konstante ist. Dies ist eine Gauss-Kurve. Die Linienbreite wird bei der halben Maximalamplitude gemessen.

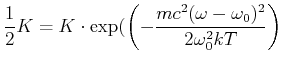
    $\displaystyle \frac{1}{2}K =K\cdot \exp(\left(-\frac{m c^2 (\omega-\omega_0)^2}{2\omega_0^2 k T}\right)$

    und

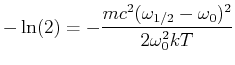
    $\displaystyle -\ln(2) = -\frac{m c^2 (\omega_{1/2}-\omega_0)^2}{2\omega_0^2 k T}$

    und

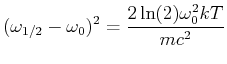
    $\displaystyle (\omega_{1/2}-\omega_0)^2 = \frac{2\ln(2)\omega_0^2 k T}{m c^2}$

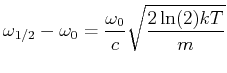
    $\displaystyle \omega_{1/2}-\omega_0 = \frac{\omega_0}{c}\sqrt{\frac{2\ln(2) k T}{m }}$

    Die ganze Linienbreite ist doppelt so gross

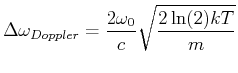
    $\displaystyle \Delta \omega_{Doppler} = \frac{2\omega_0}{c}\sqrt{\frac{2\ln(2) k T}{m }}$

    Die relative Verbreiterung ist

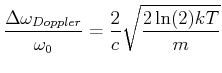
    $\displaystyle \frac{\Delta \omega_{Doppler}}{\omega_0}= \frac{2}{c}\sqrt{\frac{2\ln(2) k T}{m }}$

    und

    $\displaystyle \frac{\Delta \omega_{Doppler}}{\omega_0} = \frac{2}{3\cdot 10^8}\... ... 1.38\cdot 10^{-23} 500 K}{m/[kg] }} =6.5\cdot 10^{-19} \sqrt{kg}\cdot m^{-1/2}$


next_inactive up previous
Up: PHYS4100 Grundkurs IV  Skript:  PDF-Datei
Othmar Marti
Experimentelle Physik
Universiät Ulm