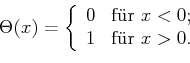

Up: PHYS4100 Grundkurs IV
Skript: PDF-Datei
Übungsblatt 10
PHYS4100 Grundkurs IV (Physik, Wirtschaftsphysik, Physik Lehramt)
Othmar Marti, (othmar.marti@uni-ulm.de)
Date: 30. 6. 2005 oder 1. 7. 2005
- Zeigen Sie, dass eine geschlossene
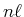 -Schale notwendigerweise
-Schale notwendigerweise 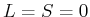 aufweisen muss.
aufweisen muss.
- Welche Atomsorte oder welche Atomsorten haben eine zu
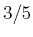 gefüllte
gefüllte 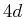 Schale? Welche Schalen sind
ganz gefüllt? Welche Elektronenkonfiguration haben diese Atome?
Schale? Welche Schalen sind
ganz gefüllt? Welche Elektronenkonfiguration haben diese Atome?
- Zwei äquivalente
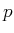 -Elektronen seinen stark Spin-Bahn-gekoppelt. Bestimmen Sie die möglichen Werte
des Gesamtdrehimpulses
-Elektronen seinen stark Spin-Bahn-gekoppelt. Bestimmen Sie die möglichen Werte
des Gesamtdrehimpulses 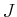 bei
bei 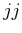 -Kopplung. Welches Prinzip muss beachtet werden?
-Kopplung. Welches Prinzip muss beachtet werden?
- Welche
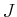 ergäben sich bei Russell-Saunders-Kopplung?
ergäben sich bei Russell-Saunders-Kopplung?
- Vergleichen Sie die Häufigkeit des Vorkommens der verschiedenen
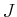 -Werte in den beiden Fällen!
-Werte in den beiden Fällen!
- Bestimmen Sie die Terme der Konfiguration
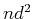 . Welcher Term stellt den Grundzustand des Titan dar?
Wie gross sind
. Welcher Term stellt den Grundzustand des Titan dar?
Wie gross sind 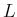 ,
, 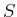 ,
, 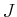 für diesen Zustand.
für diesen Zustand.
- Zeigen Sie, dass für eine endliche Temperatur der angeregte Zustand eines Zweiniveau-Systems immer
schwächer besetzt ist als der Grundzustand.
- Diskutieren Sie die minimal mögliche Linienbreite einer Spektrallinie. Welche Einflüsse verbreitern
diese Linien. Wie gross ist die natürliche Linienbreite von ``verbotenen'' Übergängen.
- Ein Laserpuls wird durch
dargestellt. Welche Frequenzbandbreite hat dieser Puls? Wovon hängt die Bandbreite ab? Wie hängt die
Bandbreite im Frequenzraum und die örtliche Breite zusammen?
- Man betrachtet ein Atom mit mehreren Valenzelektronen und vernachlässigt die Wechselwirkung
untereinander und die Spin-Bahn-Wechselwirkung. Jeder Einelektronenzustand wird durch
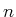 ,
, 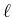 ,
, 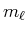 ,
,
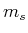 . Die Wellenfunktion des Atoms ist dann
. Die Wellenfunktion des Atoms ist dann
- Das Element ist Technetium (
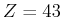 ) Ganz gefüllt sind die Schalen
) Ganz gefüllt sind die Schalen 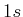 ,
, 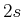 ,
, 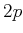 ,
, 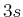 ,
, 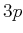 ,
, 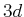 ,
,
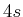 ,
, 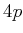 . zu
. zu 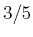 gefüllt ist die
gefüllt ist die 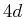 -Schale. Die
-Schale. Die 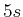 -Schale ist mit einem Elektron gefüllt.
Für die
-Schale ist mit einem Elektron gefüllt.
Für die 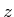 -Komponenten des Bahndrehimpulses und des Spins ist
Ist eine
-Komponenten des Bahndrehimpulses und des Spins ist
Ist eine 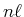 -Schale ganz gefüllt, dann sind nach Pauli alle möglichen Zustände besetzt. Insbesondere wird
zu jedem Wert der
-Schale ganz gefüllt, dann sind nach Pauli alle möglichen Zustände besetzt. Insbesondere wird
zu jedem Wert der 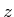 -Komponente auch der entsprechende negative Wert realisiert. Die Gesamtwellenfunktion
besteht aus
-Komponente auch der entsprechende negative Wert realisiert. Die Gesamtwellenfunktion
besteht aus 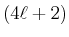 Zuständen. Sie ist auch eine Eigenfunktion des Gesamtbahndrehimpulses und des
Gesamtspins. Deshalb ist
Zuständen. Sie ist auch eine Eigenfunktion des Gesamtbahndrehimpulses und des
Gesamtspins. Deshalb ist
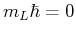 und
und
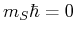 . Also kann nur
. Also kann nur 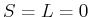 sein.
sein.
- Ein Elektron wird durch
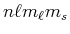 angegeben. Bei zwei Elektronen dürfen nach Pauli nicht beide
Elektronen in allen Zuständen übereinstimmen. Bei einer
angegeben. Bei zwei Elektronen dürfen nach Pauli nicht beide
Elektronen in allen Zuständen übereinstimmen. Bei einer 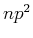 Konfiguration ergeben sich die folgenden
Möglichkeiten
Konfiguration ergeben sich die folgenden
Möglichkeiten
|
|
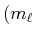 , ,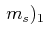 |
| |
|
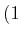 , ,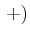 |
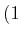 , ,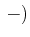 |
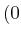 , ,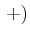 |
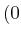 , ,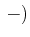 |
(
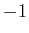 , ,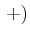 |
(
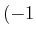 , ,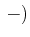 |
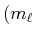 , ,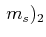 |
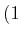 , ,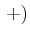 |
 |
x |
x |
x |
x |
x |
| |
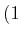 , ,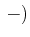 |
 |
 |
x |
x |
x |
x |
| |
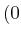 , ,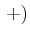 |
 |
 |
 |
x |
x |
x |
| |
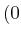 , ,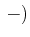 |
 |
 |
 |
 |
x |
x |
| |
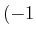 , ,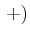 |
 |
 |
 |
 |
 |
x |
| |
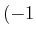 , ,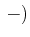 |
 |
 |
 |
 |
 |
 |
Ein Zustand wird durch
![$ \left[(m_{\ell_1}\text{,} m_{s_1})(m_{\ell_2}\text{,} m_{s_2})\right]$](img46.gif) angegeben.
Zwei Drehimpulse
angegeben.
Zwei Drehimpulse
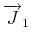 und
und
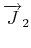 ergeben den Gesamtdrehimpuls
ergeben den Gesamtdrehimpuls
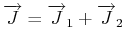 mit den Werten
mit den Werten
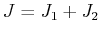 ,
,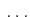 ,
,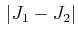 und den zugehörigen
und den zugehörigen 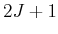 -Werten
-Werten 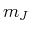 .
Es gilt
.
Es gilt
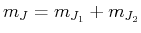 . Aus den Zuständen
. Aus den Zuständen
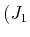 ,
,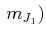 und
und
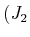 ,
,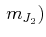 ergibt sich
formal der Zustand
ergibt sich
formal der Zustand
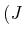
,
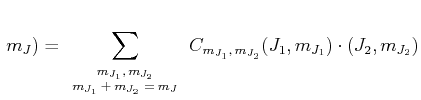
wobei nach der Kopplung 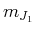 und
und 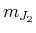 keine brauchbaren Quantenzahlen mehr sind. Ein
2-Elektronenzustand wird durch die Quantenzahlen
keine brauchbaren Quantenzahlen mehr sind. Ein
2-Elektronenzustand wird durch die Quantenzahlen
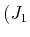 ,
,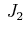 ,
,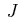 ,
,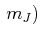 festgelegt.
festgelegt.
- Bei der
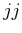 -Kopplung sind die Pauli-verträglichen Kombinationen aus der oberen Tabelle:
-Kopplung sind die Pauli-verträglichen Kombinationen aus der oberen Tabelle:
 |
 |
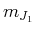 |
 |
 |
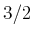 |
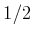 |
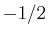 |
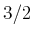 |
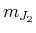 |
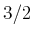 |
 |
 |
 |
 |
 |
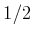 |
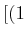 , ,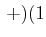 , ,![$ -)]$](img72.gif) |
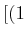 , ,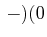 , ,![$ +)]$](img74.gif) |
 |
 |
 |
 |
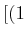 , ,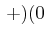 , ,![$ +)]$](img74.gif) |
 |
 |
|
 |
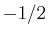 |
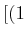 , ,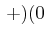 , ,![$ -)]$](img72.gif) |
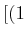 , ,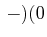 , ,![$ -)]$](img72.gif) |
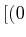 , ,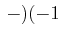 , ,![$ +)]$](img74.gif) |
 |
 |
 |
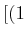 , ,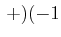 , ,![$ +)]$](img74.gif) |
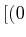 , ,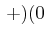 , ,![$ -)]$](img72.gif) |
 |
 |
 |
 |
 |
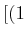 , ,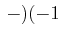 , ,![$ +)]$](img74.gif) |
|
|
 |
 |
 |
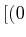 , ,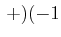 , ,![$ -)]$](img72.gif) |
|
|
 |
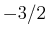 |
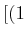 , ,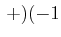 , ,![$ -)]$](img72.gif) |
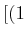 , ,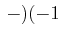 , ,![$ -)]$](img72.gif) |
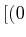 , ,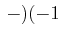 , ,![$ -)]$](img72.gif) |
 |
 |
 |
 |
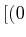 , ,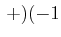 , ,![$ -)]$](img72.gif) |
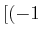 , ,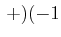 , ,![$ -)]$](img72.gif) |
 |
wobei 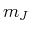 aus der Summe der
aus der Summe der 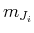 berechnet wird.
Die
berechnet wird.
Die 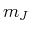 treten mit der folgenden Häufigkeit auf
treten mit der folgenden Häufigkeit auf
Es gibt also 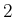 Zustände mit
Zustände mit 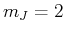 . Dieser Zustand kann nur zu
. Dieser Zustand kann nur zu 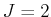 gehören. Deshalb sind jeweils zwei
der Zustande zu den kleineren
gehören. Deshalb sind jeweils zwei
der Zustande zu den kleineren 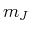 zu
zu 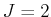 gehörig. Ohne diese Zustände sieht die Tabelle so aus
gehörig. Ohne diese Zustände sieht die Tabelle so aus
Es gibt also einen Zustand mit 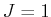 . Es bleiben noch zwei
. Es bleiben noch zwei 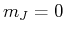 -Zustände, die zu
-Zustände, die zu 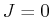 gehören. Es gibt
also die folgenden
gehören. Es gibt
also die folgenden 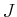 s:
s:
- Bei der LS-Kopplung müssen zuerst die Bahndrehimpulse und die Spins addiert werden.
Die Pauli-verträglichen Kombinationen aus der oberen Tabelle sind :
 |
 |
 |
 |
 |
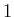 |
0 |
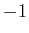 |
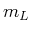 |
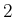 |
 |
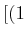 , ,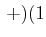 , ,![$ -)]$](img72.gif) |
 |
 |
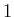 |
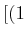 , ,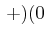 , ,![$ +)]$](img74.gif) |
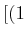 , ,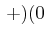 , ,![$ -)]$](img72.gif) |
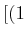 , ,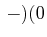 , ,![$ -)]$](img72.gif) |
 |
 |
 |
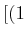 , ,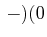 , ,![$ +)]$](img74.gif) |
 |
 |
0 |
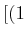 , ,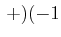 , ,![$ +)]$](img74.gif) |
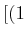 , ,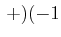 , ,![$ -)]$](img72.gif) |
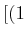 , ,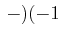 , ,![$ -)]$](img72.gif) |
 |
 |
 |
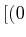 , ,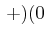 , ,![$ -)]$](img72.gif) |
 |
 |
 |
 |
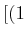 , ,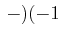 , ,![$ +)]$](img74.gif) |
 |
 |
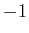 |
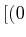 , ,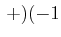 , ,![$ +)]$](img74.gif) |
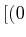 , ,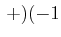 , ,![$ -)]$](img72.gif) |
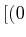 , ,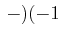 , ,![$ -)]$](img72.gif) |
 |
 |
 |
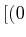 , ,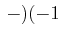 , ,![$ +)]$](img74.gif) |
 |
 |
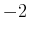 |
 |
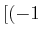 , ,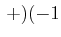 , ,![$ -)]$](img72.gif) |
 |
wobei 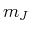 aus der Summe der
aus der Summe der 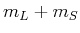 berechnet wird.
Die
berechnet wird.
Die 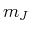 treten mit der folgenden Häufigkeit auf
treten mit der folgenden Häufigkeit auf
Es gibt also 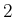 Zustände mit
Zustände mit 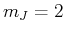 . Dieser Zustand kann nur zu
. Dieser Zustand kann nur zu 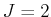 gehören. Deshalb sind jeweils zwei
der Zustande zu den kleineren
gehören. Deshalb sind jeweils zwei
der Zustande zu den kleineren 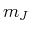 zu
zu 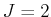 gehörig. Ohne diese Zustände sieht die Tabelle so aus
gehörig. Ohne diese Zustände sieht die Tabelle so aus
Es gibt also einen Zustand mit 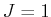 . Es bleiben noch zwei
. Es bleiben noch zwei 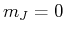 -Zustände, die zu
-Zustände, die zu 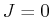 gehören. Es gibt
also die folgenden
gehören. Es gibt
also die folgenden 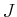 s:
s:
- Ein
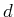 -Zustand hat den Drehimpuls
-Zustand hat den Drehimpuls 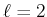 . Der Gesamtdrehimpuls ist also zwischen 0 und
. Der Gesamtdrehimpuls ist also zwischen 0 und 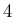 . Der
Spin muss bei geradem
. Der
Spin muss bei geradem 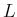 antiparallel sein. Also ist
antiparallel sein. Also ist
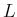 |
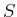 |
Terme |
Anzahl der Zustände |
| 4 |
0 |
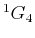 |
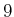 |
| 3 |
1 |
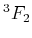 , , 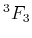 , , 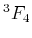 |
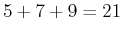 |
| 2 |
0 |
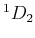 |
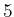 |
| 1 |
1 |
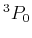 , , 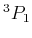 , , 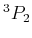 |
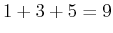 |
| 0 |
0 |
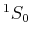 |
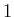 |
Aus den Hundschen Regeln folgt für den Grundzustand
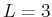 ,
, 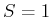 ,
, 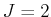 , also
, also 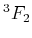
- Die Besetzungszahl eines Niveaus
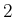 mit der Energie
mit der Energie
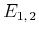 relativ zu einem Niveau
relativ zu einem Niveau 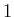 ist nach
Boltzmann
Entsprechend ist die Besetzungszahl des Niveaus
ist nach
Boltzmann
Entsprechend ist die Besetzungszahl des Niveaus 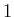 wenn die Gesamtzahl der Atome
wenn die Gesamtzahl der Atome 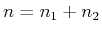 ist, hat man auch
Zusammen also
ist, hat man auch
Zusammen also
- Die Linienbreite von Atomen oder Molekülen hängt von
- der Geschwindigkeitsverteilung und deshalb von der Temperatur ab
- Sie hängt vom Druck ab (jeder Stoss ermöglicht einen Übergang, die Lebensdauer der angeregten
Niveaux sinkt deshalb).
- Die natürliche Linienbreite hängt von der Lebensdauer des angeregten Niveaux ab.
Verbotene Übergänge haben eine sehr lange Lebensdauer und deshalb eine sehr kleine Linienbreite, immer viel schmaler als erlaubte Übergänge.
- Die Umhüllende des Pulses ist
Der Ort des Pulses ist demnach
Im mitbewegten Koordinatensystem ist
Die Fouriertransformation ist
wobei
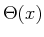 die Heaviside-Funktion ist.
Die Bandbreite ist also
die Heaviside-Funktion ist.
Die Bandbreite ist also 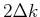 . Mit der Dispersionsrelation
. Mit der Dispersionsrelation
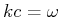 bekommt man die Frequenzbreite
Die Breite hängt von den ersten Minimas der
bekommt man die Frequenzbreite
Die Breite hängt von den ersten Minimas der 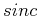 -Funktion ab. Diese liegen bei
-Funktion ab. Diese liegen bei
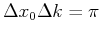 .
Dies ist auch die gesuchte Beziehung
Bemerkung: Wenn Sie mit Maple rechnen ergibt evalm oft eine wesentliche Vereinfachung der Terme.
.
Dies ist auch die gesuchte Beziehung
Bemerkung: Wenn Sie mit Maple rechnen ergibt evalm oft eine wesentliche Vereinfachung der Terme.


Up: PHYS4100 Grundkurs IV
Skript: PDF-Datei
Othmar Marti
Experimentelle Physik
Universiät Ulm
 -Elektronen seinen stark Spin-Bahn-gekoppelt. Bestimmen Sie die möglichen Werte
des Gesamtdrehimpulses
-Elektronen seinen stark Spin-Bahn-gekoppelt. Bestimmen Sie die möglichen Werte
des Gesamtdrehimpulses 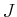 bei
bei 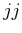 -Kopplung. Welches Prinzip muss beachtet werden?
-Kopplung. Welches Prinzip muss beachtet werden?
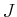 ergäben sich bei Russell-Saunders-Kopplung?
ergäben sich bei Russell-Saunders-Kopplung?
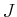 -Werte in den beiden Fällen!
-Werte in den beiden Fällen!
![$\displaystyle E(x,t)=E_0 e^{-i\omega_0 t+ i k_0 x}\cdot \frac{2\sin\left[(\omega' t-x)\Delta k\right]}{\omega't -
x}$](img11.gif)
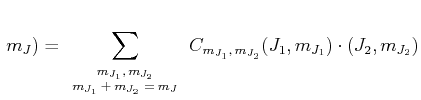
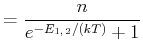
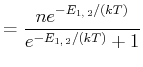
![$\displaystyle \hat{E}(x)=E_0 \frac{2\sin\left[(\omega' t-x)\Delta k\right]}{\omega't -
x}$](img122.gif)
![$\displaystyle \hat{E}(x_0)=E_0 \frac{2\sin\left[x_0\Delta k\right]}{x_0}$](img124.gif)