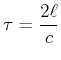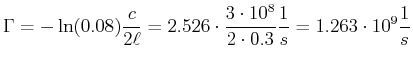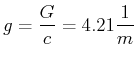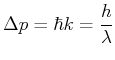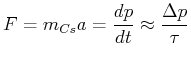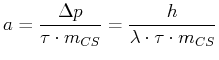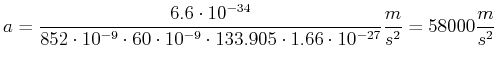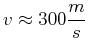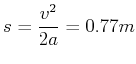

Up: PHYS4100 Grundkurs IV
Skript: PDF-Datei
Übungsblatt 11
PHYS4100 Grundkurs IV (Physik, Wirtschaftsphysik, Physik Lehramt)
Othmar Marti, (othmar.marti@uni-ulm.de)
Date: 7. 7. 2005 oder 8. 7. 2005
- Wie heiss muss ein perfekter schwarzer Strahler mit
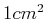 Fläche sein, um mit einem Filter der
Breite
Fläche sein, um mit einem Filter der
Breite 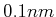 die gleiche Strahlungsstärke wie ein HeNe-Laser (
die gleiche Strahlungsstärke wie ein HeNe-Laser (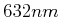 ) zu haben? Der Laserstrahl habe eine
Divergenz von
) zu haben? Der Laserstrahl habe eine
Divergenz von 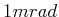 .
.
- Zeigen Sie aus der Ableitung des Planckschen Gesetzes nach Einstein, dass ein UV-Laser schwerer zu
realisieren ist als ein IR-Laser.
- Wie gross ist der Verstärkungskoeffizient (in
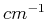 ) entlang des Lichtwegs in einem
) entlang des Lichtwegs in einem 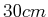 langen
HeNe-Laser, wenn dieser bei einer Reflexion des Auskoppelspiegels von von weniger als
langen
HeNe-Laser, wenn dieser bei einer Reflexion des Auskoppelspiegels von von weniger als 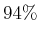 erlischt? Wie
könnte man die Ausgangsleistung erhöhen?
erlischt? Wie
könnte man die Ausgangsleistung erhöhen?
- Ein Atom erfährt durch die Absorption von Photonen aus einem Laserstrahl einen Rückstoss. Die spontane
Emission geschieht in alle Richtungen, verursacht also im Mittel keinen Impulsübertrag. Wie gross ist die
maximale Beschleunigung für ein Cäsium-Atom, das Licht bei
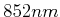 absorbiert und maximal ein Photon pro
absorbiert und maximal ein Photon pro 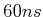 streuen kann? Wie lange ist die Bremsstrecke für thermische Cäsiumatome?
streuen kann? Wie lange ist die Bremsstrecke für thermische Cäsiumatome?
- Wir verwenden das Plancksche Strahlungsgesetz.
Die schwarze Fläche
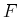 strahlt in einen Halbraum (
strahlt in einen Halbraum (
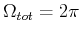 ) ab. Der Laser mit der
Leistung
) ab. Der Laser mit der
Leistung 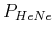 strahlt aber in den Raumwinkel
strahlt aber in den Raumwinkel
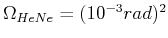 .
Aus dem weissen Spektrum des schwarzen Strahlers wird ein Frequenzband mit der Breite
herausgeschnitten.
Die Temperatur erhält man aus
.
Aus dem weissen Spektrum des schwarzen Strahlers wird ein Frequenzband mit der Breite
herausgeschnitten.
Die Temperatur erhält man aus
und
also
- Bei einem Laser ist die Rate der spontanen Emission proportional zu
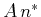 , die der induzierten
Emission
, die der induzierten
Emission
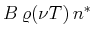 . Im thermischen Gleichgewicht ist
nach Aufgabe 2, Übungsblatt 3
. Im thermischen Gleichgewicht ist
nach Aufgabe 2, Übungsblatt 3
![\includegraphics[width=0.5\textwidth]{ue11-01.eps}](img32.gif)
Die Grafik zeigt, dass die induzierte Emission bei kleinen 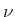 dominiert.
dominiert.
- Die Umlaufszeit im Resonator ist
Bei jedem Umlauf entsteht ein Verlust von
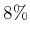 .
Der Verlust bei einem Umlauf ist
mit
.
Der Verlust bei einem Umlauf ist
mit
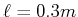 .
Also ist
Die Verstärkung
.
Also ist
Die Verstärkung 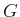 muss die Verluste kompensieren. Also ist
Die Geschwindigkeit des Lichtes im Gas ist etwa
muss die Verluste kompensieren. Also ist
Die Geschwindigkeit des Lichtes im Gas ist etwa 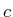 . Also ist die Verstärkung pro Länge gegeben durch
. Also ist die Verstärkung pro Länge gegeben durch
- Jedes Photon ergibt im Mittel einen Impulsübertrag von
Die Kraft auf eine Masse
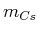 ist
wobei
ist
wobei 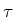 die mittlere Lebensdauer ist.
Also ist die Beschleunigung
und
Thermische Cäsium-Atome haben eine Geschwindigkeit von
Die Bremsstrecke ist aus
die mittlere Lebensdauer ist.
Also ist die Beschleunigung
und
Thermische Cäsium-Atome haben eine Geschwindigkeit von
Die Bremsstrecke ist aus
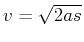


Up: PHYS4100 Grundkurs IV
Skript: PDF-Datei
Othmar Marti
Experimentelle Physik
Universiät Ulm
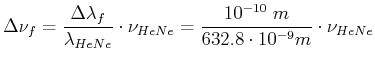
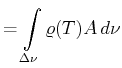
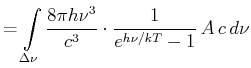
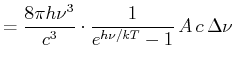
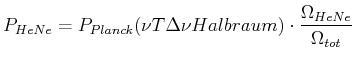
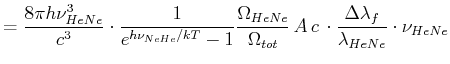
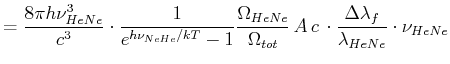
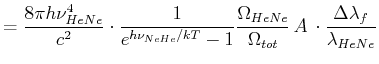
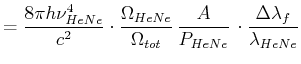
![$\displaystyle = \ln\left[\frac{8\pi h \nu_{HeNe}^4}{c^2}\cdot \frac{\Omega_{HeN...
...}\, \frac{A}{P_{HeNe}}\, \cdot \frac{\Delta \lambda_f}{\lambda_{HeNe}}+1\right]$](img26.gif)
![$\displaystyle = \frac{h\nu_{NeHe}}{k\ln\left[\frac{8\pi h \nu_{HeNe}^4}{c^2}\cd...
...\, \frac{A}{P_{HeNe}}\, \cdot \frac{\Delta \lambda_f}{\lambda_{HeNe}}+1\right]}$](img28.gif)
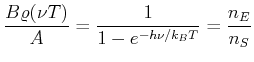
![\includegraphics[width=0.5\textwidth]{ue11-01.eps}](img32.gif)