Weiter: Mechanik deformierbarer Medien Oben: Mechanik starrer Körper Zurück: Kreisel Skript: PDF-Datei Übungen: Blätter ILIAS: Materialien Korrekturen
Wenn Maschinen im Gleichgewicht sind, können Kräfte über virtuelle Verrückungen aus dem Energiesatz berechnet werden.
Virtuell heisst, die Bewegungen müssen mit den Zwangsbedingungen vereinbar sein. Das bedeutet, dass
bei einer durch Führungen vorgegebenen Bahn (Wasserrutsche im Schwimmbad) alle betrachteten
Bewegungen dem Weg der Wasserrutsche folgen müssen. Wir betrachten zuerst einmal alle Teile des
Systems als unabhängig. Die verschiedenen möglichen Verschiebungen ![]() sind dann durch die
Koordinaten
sind dann durch die
Koordinaten ![]() gegeben. Diese werden zuerst als unabhängig angesehen. Die Energieerhaltung
fordert aber, dass
gegeben. Diese werden zuerst als unabhängig angesehen. Die Energieerhaltung
fordert aber, dass
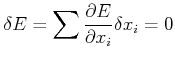 |
(6.635) |
ist.
Dabei ist
![]() die Gleichgewichtsbedingung.
die Gleichgewichtsbedingung.
![\includegraphics[width=0.4\textwidth]{starr-026}](img2599.gif)
Flaschenzug: Berechnung mit virtuellen Verschiebungen.
|
|
|
Wir betrachten als Beispiel einen Flaschenzug. ![]() sei die potentielle Energie als Funktion der Koordinaten
sei die potentielle Energie als Funktion der Koordinaten
![]() und
und ![]() . Wir haben also
. Wir haben also
mit
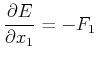 |
(6.636) |
Wir setzen die Beziehung zwischen
![]() und
und
![]() ein
ein
Die gefundene Beziehung ist unabhängig von
![]() . Also
hat man
. Also
hat man
oder
![]() .
.
Ein zweites Beispiel ist die Kurbelwelle und der Pleuel eines Motors.
![\includegraphics[width=0.55\textwidth]{starr-027}](img2610.gif)
Kurbelwelle und Pleuel berechnet mit virtuellen Verschiebungen.
|
|
|
Für die virtuellen Verrückungen (Arbeit) bekommt man
Weiter verwenden wir die Beziehung zwischen den Grössen
Daraus kann ![]() als Funktion von
als Funktion von ![]() dargestellt werden.
dargestellt werden.
und für die virtuelle Verschiebung
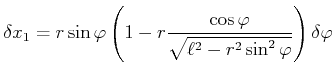
Also ist die Kraft auf die Kurbelwelle
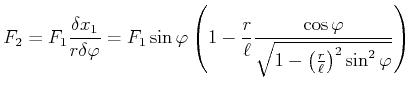 |
(6.637) |
Wenn ![]() ist, dann ist
ist, dann ist
![]() .
.
Othmar Marti