Weiter: Flüssigkeiten und Gase Oben: Mechanik deformierbarer Medien Zurück: Mechanik deformierbarer Medien Skript: PDF-Datei Übungen: Blätter ILIAS: Materialien Korrekturen
(Siehe Tipler, Physik [Tip94, pp. 342]) (Siehe Gerthsen, Physik [Mes04, pp. 130])
Wir betrachten zuerst allgemein, welche Kräfte auf einen Würfel wirken können. Beliebige Körper kann man sich im Sinne der Finiten Elemente Rechnung aus Würfeln zusammengesetzt denken.
![\includegraphics[width=0.6\textwidth]{anisotropie-spannung}](img2619.gif)
Allgemeine Kräfte an einem Würfel
|
An einem Würfel, der parallel zu den Achsen eines kartesischen Koordinatensystems liegt, können im allgemeinen Falle die folgenden Kräfte oder Spannungen sowie Deformationen auftreten:
Formal können wir schreiben
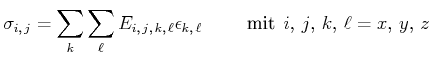 |
(7.638) |
Der Würfel soll drehmomentenfrei sein. Das Drehmoment um die ![]() -Achse kann durch das Kräftepaar
auf in der
-Achse kann durch das Kräftepaar
auf in der ![]() -Richtung auf der
-Richtung auf der ![]() -Fläche oder durch das Kräftepaar in die
-Fläche oder durch das Kräftepaar in die ![]() -Richtung auf der
-Richtung auf der
![]() -Fläche herrühren. Wenn die beiden Kräfte positiv sind, erzeugen sie ein entgegengesetztes
Drehmoment und garantieren, dass und kein Netto-Drehmoment um die
-Fläche herrühren. Wenn die beiden Kräfte positiv sind, erzeugen sie ein entgegengesetztes
Drehmoment und garantieren, dass und kein Netto-Drehmoment um die ![]() -Achse existiert.
Analog kann man mit den beiden anderen möglichen Drehachsen argumentieren. Deshalb sind von den
-Achse existiert.
Analog kann man mit den beiden anderen möglichen Drehachsen argumentieren. Deshalb sind von den ![]() Kräften
Kräften
![]() gilt
gilt
Es bleiben sechs unabhängige Kräfte (
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ). Es gibt also 6 unabhängige Spannungen (
). Es gibt also 6 unabhängige Spannungen (
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ).
).
Von den neun Deformationen
![]() sind sechs unabhängig. Die Deformationen mit den gleichen Indizes
bedeuten Dehnungen und Stauchungen. Die anderen sechs bedeuten Scherungen. So beschreibt die
sind sechs unabhängig. Die Deformationen mit den gleichen Indizes
bedeuten Dehnungen und Stauchungen. Die anderen sechs bedeuten Scherungen. So beschreibt die
![]() die Scherung der
die Scherung der ![]() -Achse gegen die
-Achse gegen die ![]() -Achse, also die Änderung des Zwischenwinkels zwischen beiden Achsen.
-Achse, also die Änderung des Zwischenwinkels zwischen beiden Achsen.
![]() beschreibt die Scherung der
beschreibt die Scherung der ![]() -Achse gegen der
-Achse gegen der ![]() -Achse, also auch die Änderung des
Zwischenwinkels. Dies ist aber in beiden Fällen der gleiche Winkel. Also gilt
-Achse, also auch die Änderung des
Zwischenwinkels. Dies ist aber in beiden Fällen der gleiche Winkel. Also gilt
![]() für
für
![]() . Es bleiben also auch sechs unabhängige Deformationen (
. Es bleiben also auch sechs unabhängige Deformationen (
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ).
).
Es bleiben also noch
![]() unabhängige Komponenten im Tensor übrig.
unabhängige Komponenten im Tensor übrig.
Wenn wir berücksichtigen, dass für kleine Deformationen
![]() die potentielle Energie wie bei
jeder Feder eine quadratische Funktion der Dehnungen sein muss und dass die Spannungen durch die Ableitung dieser
Energie nach den Deformationen berechnet werden, folgt dass es noch 21 unterschiedliche Komponenten des
Elastizitätstensors gibt. Mit anderen Worten, die Deformation des allgemeinsten Materials wird durch 21 Parameter
beschrieben.
die potentielle Energie wie bei
jeder Feder eine quadratische Funktion der Dehnungen sein muss und dass die Spannungen durch die Ableitung dieser
Energie nach den Deformationen berechnet werden, folgt dass es noch 21 unterschiedliche Komponenten des
Elastizitätstensors gibt. Mit anderen Worten, die Deformation des allgemeinsten Materials wird durch 21 Parameter
beschrieben.
Je höher die Symmetrie eines Materials ist, desto weniger unabhängige Konstanten gibt es. Im Grenzfall des
isotropen Mediums bleiben zwei, ![]() und
und ![]() .
.
(Siehe Tipler, Physik [Tip94, pp. 342]) (Siehe Gerthsen, Physik [Mes04, pp. 130])
Zieht man an einem Draht (Länge ![]() , Querschnitt
, Querschnitt ![]() und Querschnittsfläche
und Querschnittsfläche
![]() ), dann
vergrössert sich die Länge um
), dann
vergrössert sich die Länge um
![]() und verringert sich (meistens) der Querschnitt um
und verringert sich (meistens) der Querschnitt um ![]() .
.
| (7.639) |
Es sind
Wir definieren nun die Spannung
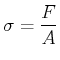 |
(7.640) |
dabei ist ![]() die an der Querschnittsfläche
die an der Querschnittsfläche ![]() wirkende Kraft.
wirkende Kraft.
Das Hookesche Gesetz verknüpft Spannung
|
![]() ist eine Materialkonstante, der Elastizitäts- oder der Dehnungsmodul (im englischen Young's Modulus genannt).
ist eine Materialkonstante, der Elastizitäts- oder der Dehnungsmodul (im englischen Young's Modulus genannt).
Einheiten
Wenn wir die obigen Gleichungen umschreiben, erhalten wir
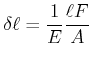 |
(7.642) |
Aus Änderung des Querschnitts und der Länge können wir die Volumenänderung berechnen. Wir setzen an, dass
![]() ist
ist
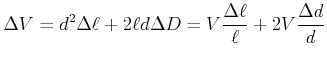 |
(7.643) |
Umgeschrieben erhalten wir
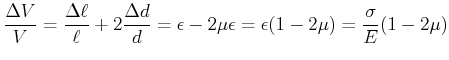 |
(7.644) |
Wir sehen, dass für positives ![]() die Poisson-Zahl der Ungleichung
die Poisson-Zahl der Ungleichung
![]() genügen muss. In
speziellen fällen kann
genügen muss. In
speziellen fällen kann ![]() auch grösser als
auch grösser als ![]() sein.
sein.
Wir haben hier ![]() und
und ![]() als Skalare angenommen.
als Skalare angenommen.
Wird der Testkörper hydrostatischem Druck ![]() unterworfen, ist also die Spannung auf allen Seiten gleich,
ändert sich das Volumen um den dreifachen Wert, der bei einer uniaxialen Spannung auftreten würde.
unterworfen, ist also die Spannung auf allen Seiten gleich,
ändert sich das Volumen um den dreifachen Wert, der bei einer uniaxialen Spannung auftreten würde.
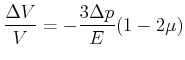 |
(7.645) |
Die Kompressibilität
![]() ist
ist
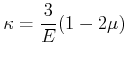 |
(7.646) |
Wird ein Draht gedehnt, kann ihm die Federkonstante
![]() zuschreiben.
zuschreiben.
Bei der Dehnung wird die Arbeit
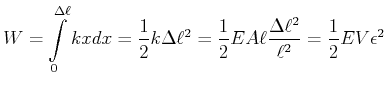 |
(7.647) |
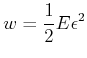 |
(7.648) |
(Siehe Gerthsen, Physik [Mes04, pp. 131])
![\includegraphics[width=0.6\textwidth]{scherung}](img2674.gif)
Scherung eines Würfels
|
Wenn die Kraft ![]() tangential zur Oberfläche steht, dann wird der Testkörper geschert. Wenn die
Stirnfläche des Würfels
tangential zur Oberfläche steht, dann wird der Testkörper geschert. Wenn die
Stirnfläche des Würfels ![]() ist, ist die Schubspannung
ist, ist die Schubspannung
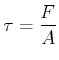 |
(7.649) |
Als Konsequenz dieser Schubspannung wird der Testkörper um den Winkel ![]() geschert.
geschert.
| (7.650) |
Einheiten
![]() ist der Schub- oder Torsionsmodul (englisch: shear modulus)
ist der Schub- oder Torsionsmodul (englisch: shear modulus)
Analog zur Energiedichte der axialen Deformation kann auch für die Scherenergiedichte
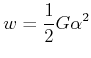 |
(7.651) |
(Siehe Gerthsen, Physik [Mes04, pp. 131])
![\includegraphics[width=0.4\textwidth]{drillung}](img2678.gif)
Verdrillung. Zur Berechnung wird
der Draht in koaxiale Zylinder unterteilt.
|
Hier verdrehen zwei entgegengesetzte Drehmomente ![]() einen Draht um den Winkel
einen Draht um den Winkel ![]() . Ein Hohlzylinder mit dem
Radius
. Ein Hohlzylinder mit dem
Radius ![]() un der Dicke
un der Dicke ![]() wird um
wird um
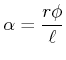 |
(7.652) |
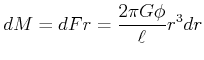 |
(7.653) |
Das gesamte Drehmoment erhalten wir durch Integration
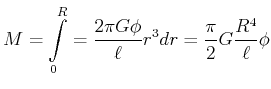 |
(7.654) |
Wir können dem Draht die Richtgrösse
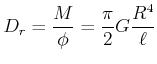 |
(7.655) |
(Siehe Gerthsen, Physik [Mes04, pp. 134])
![\includegraphics[width=0.6\textwidth]{biegebalken}](img2687.gif)
Biegebalken
|
Biegebalken werden heute in vielen die Oberflächen abtastenden Instrumenten eingesetzt. Als Stimmgabeln sind sie die zeitbestimmenden Elemente in einer Uhr.
Der Balken der Länge ![]() , Breite
, Breite ![]() und Dicke
und Dicke ![]() soll einseitig eingespannt sein. Wir legen am Ende eine
Kraft
soll einseitig eingespannt sein. Wir legen am Ende eine
Kraft ![]() an, die senkrecht zur ursprünglichen Lage des Balkens sein soll. An einem Punkt im Abstand
an, die senkrecht zur ursprünglichen Lage des Balkens sein soll. An einem Punkt im Abstand ![]() vom Balkenende ist als Wirkung der Kraft der Balken gebogen, und zwar mit einem Krümmungsradius von
vom Balkenende ist als Wirkung der Kraft der Balken gebogen, und zwar mit einem Krümmungsradius von ![]() .
Die oberen Schichten werden um
.
Die oberen Schichten werden um
![]() gedehnt, die unteren entsprechend gestaucht. In der Mitte befindet
sich (rot eingezeichnet) die neutrale Faser Gemittelt über die obere Hälfte des Balkenquerschnitts (über
der neutralen Faser) ist die Dehnung
gedehnt, die unteren entsprechend gestaucht. In der Mitte befindet
sich (rot eingezeichnet) die neutrale Faser Gemittelt über die obere Hälfte des Balkenquerschnitts (über
der neutralen Faser) ist die Dehnung
![]() . Die untere Hälfte ist entsprechend gestaucht. Sowohl für die
Stauchung wie auch für die Dehnung wird eine Kraft von
. Die untere Hälfte ist entsprechend gestaucht. Sowohl für die
Stauchung wie auch für die Dehnung wird eine Kraft von
![]() , und analog dazu eine Kraft für die Stauchung. Die beiden Kräfte bilden ein Kräftepaar
(Abstand
, und analog dazu eine Kraft für die Stauchung. Die beiden Kräfte bilden ein Kräftepaar
(Abstand
![]() ), das Drehmoment
), das Drehmoment
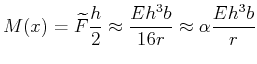 |
(7.656) |
![]() ist hier eine Schätzung und müsste mit einer ausführlicheren Rechnung berechnet werden.
Für einen rechteckigen Querschnitt zeigt die genauere Rechnung, dass
ist hier eine Schätzung und müsste mit einer ausführlicheren Rechnung berechnet werden.
Für einen rechteckigen Querschnitt zeigt die genauere Rechnung, dass
![]() und nicht
und nicht
![]() ist. Die Ursache für das Drehmoment
ist. Die Ursache für das Drehmoment ![]() ist die Kraft
ist die Kraft ![]() am Ende des
Balkens im Abstand
am Ende des
Balkens im Abstand ![]() . Wir erhalten
. Wir erhalten
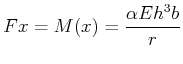 |
(7.657) |
oder
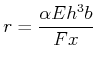 |
(7.658) |
Die Krümmung ![]() ist an der Einspannungsstelle am grössten. Die Spannung
ist an der Einspannungsstelle am grössten. Die Spannung ![]() ist
ist
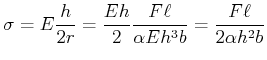 |
(7.659) |
Wird die Festigkeitsgrenze überschritten, bricht der Balken an der Einspannstelle. Die Belastbarkeit
eines einseitig eingespannten Balkens ( und auch eines zweiseitig eingespannten oder aufgestützten Balkens) geht
mit
![]() .
.
Typische Anwendungen einseitig eingespannter Balken finden sich in der Mikrosystemtechnik.
![\includegraphics[width=0.8\textwidth]{cantilever_noell}](img2702.gif)
Prinzip der Herstellung eines freitragenden,
einseitig eingespannten Balkens mit mikrotechnologischen Mitteln (W. Noell Dissertation Ulm und IMM
Mainz[Noe98, 84])
|
![\includegraphics[width=0.4\textwidth]{cantilever-rem}](img2703.gif)
![\includegraphics[width=0.4\textwidth]{cantilever-rem-tip}](img2704.gif)
REM (Rasterelektronenmikroskop)-Bilder des Balkens a) und der
Sonde b) eines AFM-Sensors (W. Noell Dissertation Ulm und IMM Mainz[Noe98, 85])
|
(Siehe Gerthsen, Physik [Mes04, pp. 132])
![\includegraphics[width=0.55\textwidth]{scherung-dehnung}](img2705.gif)
Zusammenhang zwischen Scherung und Dehnung
|
Die blau eingezeichneten Kräfte in der obigen Abbildung bewirken eine Scherung um
den Winkel ![]() des Würfels mit der Seitenfläche
des Würfels mit der Seitenfläche ![]() . Der Schermodul des Materials ist also
. Der Schermodul des Materials ist also
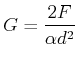
Die blauen Kräfte können jeweils in zwei halb so grosse Kräfte (rot)aufgespalten werden. Nun werden jeweils zwei roten Kräfte von zwei nebeneinander liegenden Flächen zusammengefasst; das Resultat sind die grünen Kräfte. Diese bewirken eine reine Dehnung oder Stauchung.
| Jede Scherung kann also als Kombination von einer Stauchung und einer orthogonal dazu liegenden Dehnung aufgefasst werden. |
Die eine Diagonale wird um
![]() gedehnt, die andere um den gleichen Wert gestaucht. Die Kräfte
wirken auf dreieckförmige Körper. Im Mittel ist die effektive Fläche halb so gross wie die Diagonalfläche (analog
zur Berechnung der Dreiecksfläche
gedehnt, die andere um den gleichen Wert gestaucht. Die Kräfte
wirken auf dreieckförmige Körper. Im Mittel ist die effektive Fläche halb so gross wie die Diagonalfläche (analog
zur Berechnung der Dreiecksfläche
![]() ).
).
Effektiv verwenden wir eine Fläche der Grösse
![]() . Jede der Kräfte
. Jede der Kräfte
![]() erzeugt eine
relative Dehnung oder Stauchung um
erzeugt eine
relative Dehnung oder Stauchung um
![]() in ihrer Richtung und eine Querkontraktion oder
-dilatation von
in ihrer Richtung und eine Querkontraktion oder
-dilatation von
![]() . Die Kräfte auf die beiden anderen Seiten bewirken noch einmal die
gleichen Deformationen. Beide Deformationen zusammen ergeben2.
. Die Kräfte auf die beiden anderen Seiten bewirken noch einmal die
gleichen Deformationen. Beide Deformationen zusammen ergeben2.
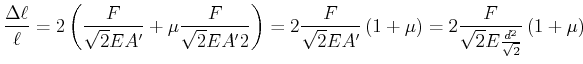
Die Deformation
![]() kann aus der Scherung berechnet werden:
kann aus der Scherung berechnet werden:
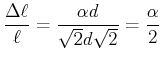
Also ist
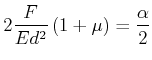
Umgestellt erhalten wir
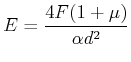
und durch Vergleich
| (7.660) |
Da die Poissonzahl
![]() ist, bekommt man auch
ist, bekommt man auch
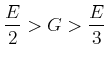 |
(7.661) |
(Siehe Gerthsen, Physik [Mes04, pp. 132])
![\includegraphics[width=0.8\textwidth]{grauguss}](img2722.gif)
Spannungs-Dehnungs-Kurven von Stahl und Grauguss
|
Bei grossen Deformationen ist die Antwort des deformierten Körpers nicht mehr linear. Wir nennen diesen Bereich auch den Nicht-Hookeschen Bereich. Im obigen Bild wird das Verhalten für Grauguss und Stahl dargestellt. Es können die folgenden Bereiche unterschieden werden:
Othmar Marti