Weiter: Skalarprodukt und Vektorprodukt in Oben: Einige notwendige mathematische Verfahren Zurück: Integration Skript: PDF-Datei Übungen: Blätter ILIAS: Materialien Korrekturen
beschreiben Orte oder gerichtete Grössen
![\includegraphics[width=0.7\textwidth]{einfuehrung-004}](img3715.gif)
Definition von Vektoren.
|
![\begin{displaymath}\overrightarrow{r}=\vec{r}=\left(
\begin{array}[c]{r}
x\\
y
\end{array}\right) \end{displaymath}](img3716.gif)
![\begin{displaymath}\overrightarrow{v}=\vec{v}=\left(
\begin{array}[c]{r}
v_{x}\\...
...eft(
\begin{array}[c]{r}
\dot{x}\\
\dot{y}
\end{array}\right)\end{displaymath}](img3717.gif)
Die Ableitung nach der Zeit wird auch als
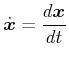
Addition:
![$\displaystyle \vec{a}+\vec{b}=\left( \begin{array}[c]{r} a_{x} a_{y} b_{z...
...egin{array}[c]{r} a_{x}+b_{x} a_{y}+b_{y} d_{z}+b_{z} \end{array} \right)$](img3719.gif) |
(C..922) |
|
|
Länge eines Vektors
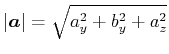 |
(C..923) |
Skalarprodukt
| (C..924) |
der Einheitsvektor
![]() ist ein Vektor der Länge
ist ein Vektor der Länge ![]() , der in die
, der in die ![]() -Richtung zeigt.
-Richtung zeigt.
Vektorprodukt
![$\displaystyle \vec{a}\times\vec{b}=\left( \begin{array}[c]{r} a_{x} a_{y} ...
..._{z}b_{y} a_{z}b_{x}-a_{x}b_{z} a_{x}b_{y}-a_{y}b_{x} \end{array} \right)$](img3722.gif) |
(C..925) |
Für die Orientierung der Vektoren gilt:
| (C..926) |
| (C..927) |
| (C..928) |
| (C..929) |
Gegeben seien zwei Vektoren ![]() und
und ![]() . Die Projektion von
. Die Projektion von ![]() auf
auf ![]() ,
das heisst, die Komponente von
,
das heisst, die Komponente von ![]() in die Richtung von
in die Richtung von ![]() ist
ist
In kartesischen Koordinaten heisst dies
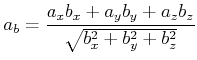 |
(C..931) |
Beispiel:
Sei
![]() und
und
![]() . Dann ist
. Dann ist
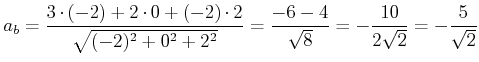 |
Beispiel:
Sei
![]() und
und
![]() . Dann ist
. Dann ist
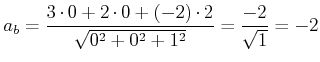 |
Othmar Marti