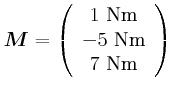- Geben Sie die Beziehung zwischen
 und
und  für die Drehung um die Radachse an.
für die Drehung um die Radachse an.
- Berechnen Sie für jeden Punkt am Umfang (Peripherie) des Rades
seinen Geschwindigkeitsvektor.
- Berechnen Sie die gesamte kinetische Energie des Rades (Bonusaufgabe).
|
|
- Wie gross ist der Massenausstoss
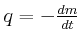 der Triebwerke?
der Triebwerke?
- Welche Leistung
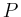 ist für die Erzeugung des Triebwerkstrahles erforderlich?
ist für die Erzeugung des Triebwerkstrahles erforderlich?
- Wie gross ist die Restmasse
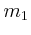 der Landesektion im Orbit?
der Landesektion im Orbit?
- Wie lange
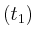 dauert die Beschleunigungsphase?
dauert die Beschleunigungsphase?
- Wie gross sind die höchste und die niedrigste Beschleunigungen
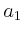 und
und 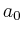 ?
?
- Welcher Anteil der von den Triebwerken gelieferten Energie ist der
Landesektion zugeführt worden (Wirkungsgrad
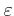 )?
)?
![]() ,
,
![]() ,
,
![]() und
und
![]()
(Die Gravitationswirkung des Mondes kann bei der Lösung dieser Aufgabe unberücksichtigt
bleiben. Die angegebene Startgeschwindigkeit reicht aus, um eine Kreisbahn in
![]() Höhe einzunehmen.)
Höhe einzunehmen.)
![]()
![]()
- Wie gross ist seine Umlaufdauer um die Sonne?
- Wie gross sind seine Bahngeschwindigkeiten
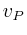 und
und 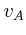 im
Perihel und Aphel?
im
Perihel und Aphel?
Die Umlaufzeit ![]() der Erde und der Erdbahnradius
der Erde und der Erdbahnradius ![]() werden als bekannt vorausgesetzt.
werden als bekannt vorausgesetzt.
![]()
![]()
- die Geschwindigkeit
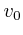 der Erde auf ihrer Bahn um die Sonne und
der Erde auf ihrer Bahn um die Sonne und
- die Masse
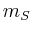 der Sonne
der Sonne
aus dem Erdbahnradius ![]() und der Umlaufdauer
und der Umlaufdauer ![]() der Erde um die Sonne bestimmen?
der Erde um die Sonne bestimmen?
- Welche Anfangsgeschwindigkeit
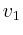 muss die Marssonde (ausserhalb
des Erdschwerefeldes) haben?
muss die Marssonde (ausserhalb
des Erdschwerefeldes) haben?
- Mit welcher Geschwindigkeit
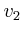 erreicht die Sonde die Marsbahn?
(Die Gravitationswirkung des Mars bleibe bis dahin unberücksichtigt.)
erreicht die Sonde die Marsbahn?
(Die Gravitationswirkung des Mars bleibe bis dahin unberücksichtigt.)
- Welche Zeit
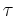 dauert der Flug der Sonde zum Mars?
dauert der Flug der Sonde zum Mars?
Kleinster Abstand Sonne - Mars:
![]()
- In welcher maximalen Entfernung
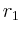 vom ersten Stern liegt das
Zentrum der Bewegung, beim maximalen Abstand?
vom ersten Stern liegt das
Zentrum der Bewegung, beim maximalen Abstand?
- Wie gross sind
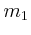 und
und 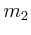 im Verhältnis zur Sonnenmasse?
im Verhältnis zur Sonnenmasse?
![]() ,
, ![]() ,
,
![]() ,
,
![]()
Wie gross ist die Gravitationskraft zwischen dem als Massenpunkt angesehen Isaac Newton
(
![]() ) und einem in
) und einem in ![]() über Newton hängenden kugelförmigen Apfel der
Masse (
über Newton hängenden kugelförmigen Apfel der
Masse (
![]() ).
).
(4 Minuten)
Gegeben sind
![\begin{displaymath}\vec{r}_{0M}=\left(
\begin{array}[c]{c}
1 \metre\\
3 \metre\\
2 \metre
\end{array}\right) \end{displaymath}](img52.gif) und
und
![\begin{displaymath}\vec{F}=\left(
\begin{array}[c]{c}
-2 \newton\\
1 \newton \\
1 \newton
\end{array}\right) \end{displaymath}](img53.gif)
- Berechnen Sie das Drehmoment
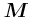 .
.
- Wir betrachten eine am Punkte
![\begin{displaymath}\left(
\begin{array}[c]{c}
0 \metre\\
0 \metre\\
0 \metre
\end{array}\right) \end{displaymath}](img55.gif) punktgespiegelte Welt. Wie gross sind dort
punktgespiegelte Welt. Wie gross sind dort
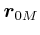 ,
, 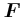 und
und
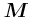 ?
?
(6 Minuten)
![\includegraphics[width=\textwidth]{ue06-01-2008}](img4.gif)
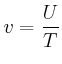
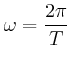
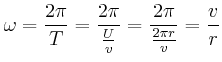
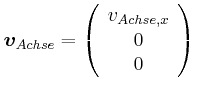
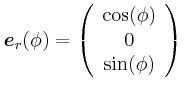
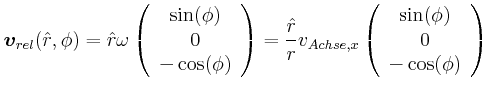
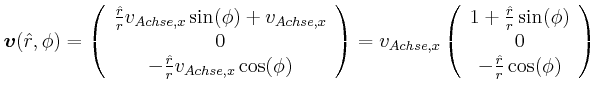
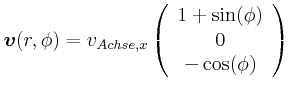
![\includegraphics[width=\textwidth]{ue06-rad-2008}](img77.gif)
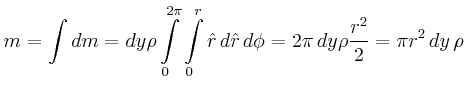
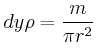
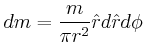
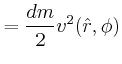
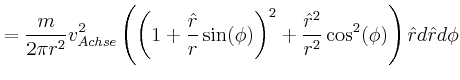
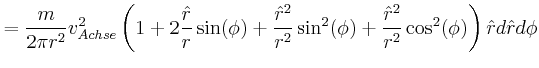
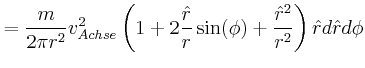
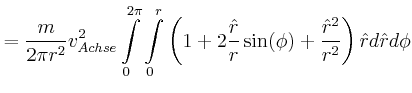
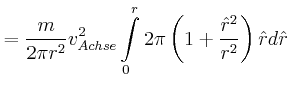
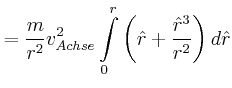
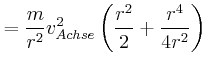
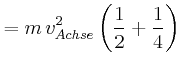
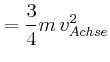
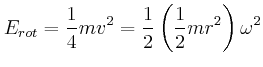
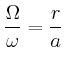
![\includegraphics[width=0.5\textwidth]{ue06-02-2008}](img108.gif)
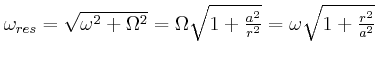
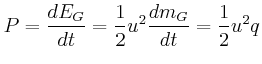
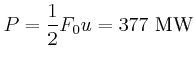
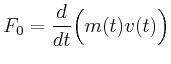
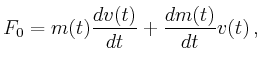
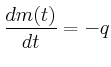
![$\displaystyle F_0 + q v(t) = \Big[ m_0 - q t \Big] \frac{d v(t)}{d t} .$](img124.gif)
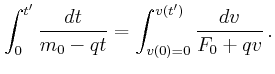
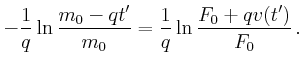
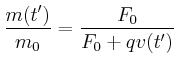
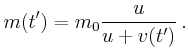
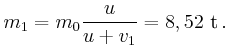
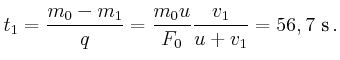
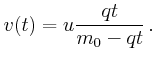
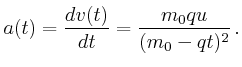
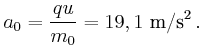
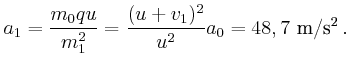
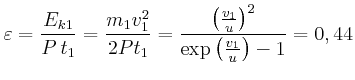
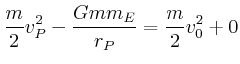
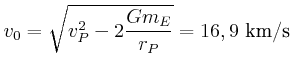

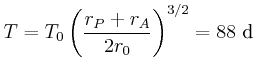
![$\displaystyle v_{P}^{2}\left[ 1-\left( \frac{r_{P}}{r_{A}}\right) ^{2}\right] =2 G
m_{S}\frac{r_{A}-r_{P}}{r_{A}r_{P}}
$](img153.gif)
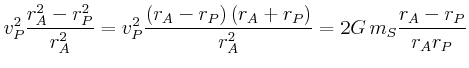
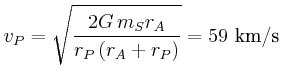
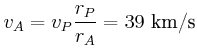
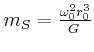
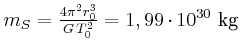
![\includegraphics[width=0.4\textwidth]{ue06-03-2008}](img165.gif)
![$ v_{1}^{2}\left[ 1-\left( \frac{r_{0}}{r_{2}}\right) ^{2}\right] =2 G
m_{S}\left( \frac{1}{r_{0}}-\frac{1}{r_{2}}\right) $](img170.gif)
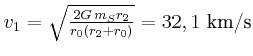
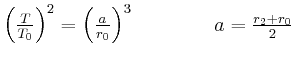
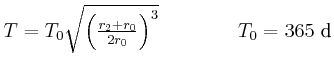
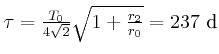
![\includegraphics[width=0.5\textwidth]{ue06-04-2008}](img178.gif)
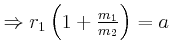
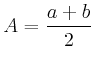
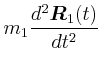
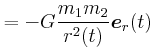
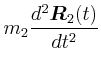
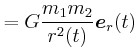
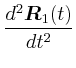
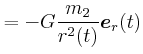
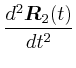
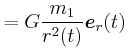
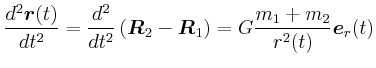
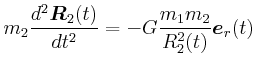
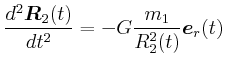
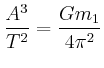
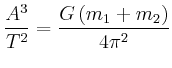
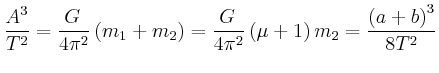
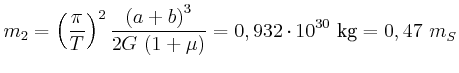
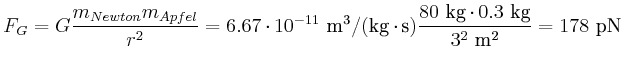
![\begin{displaymath}\vec{M}= \left(
\begin{array}[c]{c}
1 \metre\\
3 \metre ...
...\newton\metre \\
7 \newton\metre \\
\end{array} \right)
\end{displaymath}](img208.gif)
![\begin{displaymath}\vec{r}_{0M}' = \left(
\begin{array}[c]{c}
-1 \metre\\
-3 \metre\\
-2 \metre
\end{array}\right)\end{displaymath}](img209.gif)
![\begin{displaymath}\vec{F}=\left(
\begin{array}[c]{c}
2 \newton\\
-1 \newton \\
-1 \newton
\end{array}\right)\end{displaymath}](img210.gif)